标签:输出 现在 under 概率分布 image 直接 示例 nal 随机
1、训练误差和泛化误差
机器学习的主要挑战是我们的模型要在未观测数据上表现良好,而不仅仅是在训练数据上表现良好。在未观测数据上表现良好称为泛化(generalization)。
通常情况下,我们在训练数据上训练模型时会计算一些被称为训练误差(training error)的误差度量,目标是降低训练误差。由于模型要投入到实际使用,所以我们希望泛化误差(generalization,或者被称为测试误差)也尽可能的小。泛化误差被定义为新输入的误差期望。
如果训练数据和测试数据是同分布的,我们将这个共享的潜在分布称为数据生成分布,并且数据集中的样本是相互独立的话,那么我们就可以在数学上研究训练误差和测试误差之间的关系。
我们能观察到训练误差和测试误差之间的直接联系是,随机模型训练误差的期望和该模型测试误差的期望是一样的。假设我们有概率分布 \(p(x,y)\),从中重复采样生成训练集和测试集。对于某个固定的 \(ω\),训练集误差的期望恰好和测试集误差的期望一样,这是因为这两个期望的计算都使用了相同的数据集生成过程。这两种情况的唯一区别是数据集的名字不同。
当然,当我们使用机器学习算法时,我们不会提前固定参数,然后采样得到两个数据集。我们采样得到训练集,然后挑选参数去降低训练集误差,然后采样得到测试集。在这个过程中,测试误差期望会大于或等于训练误差期望。我们可以从以下两个方面优化机器学习算法的效果:
- 降低训练误差
- 缩小训练误差和泛化误差的差距
这两个方面对应着机器学习的两个主要挑战:欠拟合(underfitting)和过拟合(overfitting)。
2、欠拟合、过拟合和容量
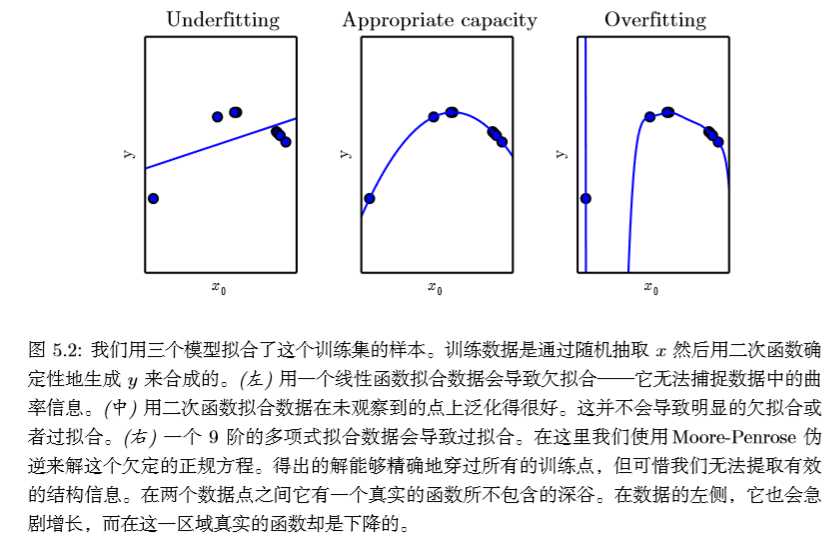
欠拟合是指模型不能在训练集上获得足够小的误差(训练误差太大),过拟合是指训练误差和泛化误差的差距太大。举个例子,假如我们从二次函数中随机取一些点,然后使用线性函数,二次函数和9阶多项式去拟合这些点,如下图:
我们可以看到线性函数会导致欠拟合,9阶函数会导致过拟合(9阶函数虽然完全拟合了这些点,但它只适用于我们取的这些点,如果在同一个二次函数上取一个新点,那么训练误差和泛化误差之间的差距会非常大),2次函数在欠拟合和过拟合之间达到了平衡。
通过控制模型的容量(capacity),我们可以控制模型是否偏向于欠拟合或者过拟合。所谓模型的容量是指其拟合各种函数的能力(可以表示多少种曲线)。容量低的模型可能很难拟合训练集,比如上例中的用线性函数去拟合二次函数。容量高的模型可能会导致过拟合,因为记住了不适用于训练集和测试集的特征(训练使用的特征太多)。
我们可以通过选择假设空间(hypothesis space)来控制模型的容量。所谓假设空间,就是学习算法可以选择为解决方案的函数集。例如,线性回归将所有关于其输入的线性函数作为假设空间。广义线性回归的假设空间除了线性函数外,还包括多项式函数,这就增加了模型的容量。模型的容量规定了机器学习算法可以从假设空间选择哪些函数族来拟合数据,这被称为模型的表示容量(representational capacity)。而事实上,学习算法一般情况下并不能找到最优的函数,而是找到一个可以大大降低训练误差的函数,这意味着学习算法的有效容量(e?ective capacity)可能小于表示容量。
当机器学习算法的容量符合任务的复杂度和训练数据的数据量时,算法一般会达到最佳效果,容量不足不能够解决复杂任务(欠拟合),容量高能够解决复杂任务,但容量过高时,就会发生过拟合,就像上面的例子一样。
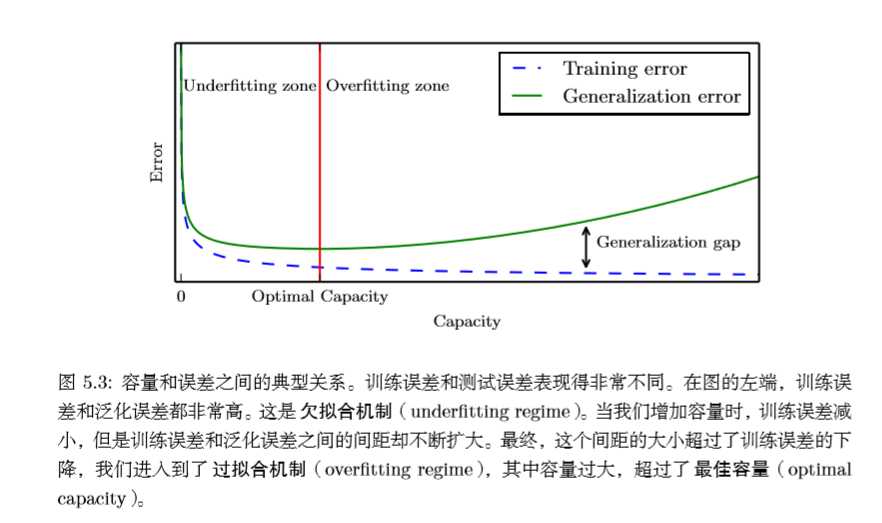
模型容量与训练误差和泛化误差有一定的关系。通常,当模型容量上升时,训练误差会降低,直至降低至最小可能误差(最小误差存在的话),而泛化误差是关于模型容量的一个U型函数,如下图
有一点需要注意,我们并不要求训练出的模型在所有的输入数据上表现良好,而只需要在满足特定分布的数据上表现良好就行,这被称为机器学习的没有免费午餐定理。
3、正则化
到现在为止,我们通过改变学习算法可选的函数来改变模型的容量进而改变机器学习算法。比如在线性回归中,我们可以增加或减少多项式的次数来改变模型的容量。但算法的效果不仅受影响于假设空间的函数数量,也取决于这些函数的具体形式。在线性函数中,对于输入和输出确实接近线性的问题,使用线性函数是很合理的,但如果输入和输出实际满足非线性函数\(y=sin(x)\),那么我们用线性函数x取拟合sin(x)的效果不会好。因此我们可以使用两种方法来控制算法的性能:
- 可以使用的函数种类
- 函数数量
例如,我们可以加入权重衰减(weight decay)来修改线性回归的训练标准。带权重衰减的线性回归最小化均方误差和正则项的和\(J(ω)\),其偏好于平方\(L^2\)范数较小的权重。具体如下:
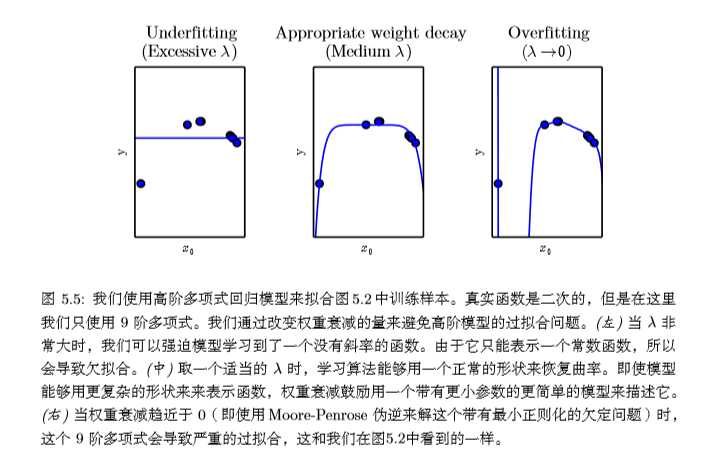
其中\(λ\)是提前挑选好的值,用来表示我们偏好范数较小权重的程度。当\(λ=0\)时,我们没有任何偏好。越大的\(λ\)偏好范数越小的权重。最小化 \(J(ω)\) 可以看作是拟合训练数据和偏好小权重范数之间的权衡。这会使得解决方案的斜率较小,或是将权重放在较少的特征上。我们可以训练具有不同 \(λ\) 值的高次多项式回归模型,来举例说明如何通过权重衰减控制模型欠拟合或过拟合的趋势。
图5.2就是第2节的第一个图。
更一般地,正则化一个学习函数\(f(x;θ)\),我们可以给代价函数添加被称为正则化项(regularizer)的惩罚。在上面的权重衰减例子中,正则化项\(Ω(ω)=ω^Tω\)。
在我们权重衰减的示例中,通过在最小化的目标中额外增加一项,我们明确地表示了偏好权重较小的线性函数。有很多其他方法隐式或显式地表示对不同解的偏好。总而言之,这些不同的方法都被称为正则化(regularization)。正则化是指我们修改学习算法,使其降低泛化误差而非训练误差。
没有免费午餐定理已经清楚地阐述了没有最优的学习算法,特别地,没有最优的正则化形式。反之,我们必须挑选一个非常适合于我们所要解决的任务的正则形式。容量、欠拟合、过拟合和正则化
标签:输出 现在 under 概率分布 image 直接 示例 nal 随机
原文地址:https://www.cnblogs.com/sench/p/9512860.html