标签：des   style   http   color   io   os   ar   for   strong   

Ellipsoid

Given a 3-dimension ellipsoid(椭球面)

your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) is defined as 

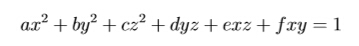
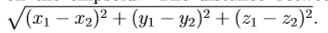
1 0.04 0.01 0 0 0

1.0000000

题目大意：

             求一个椭球面上的一个点到原点的最短距离。

解题思路：

           模拟退火，不多解释了。

解题代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

const double eps=1e-8;
const double INF=1e100;
const int offx[]={1,0,-1,0,1,-1,-1,1};
const int offy[]={0,1,0,-1,1,1,-1,-1};

double a,b,c,d,e,f;

double getAns(double x,double y){
    double A=c,B=d*y+e*x,C=a*x*x+b*y*y+f*x*y-1.0;
    double delta=B*B-4*A*C;
    if(delta<0) return INF+10;
    delta=sqrt(delta);
    double z1=(-B+delta)/(2*A),z2=(-B-delta)/(2*A);
    return min( sqrt(x*x+y*y+z1*z1) , sqrt(x*x+y*y+z2*z2)   );
}

double tosolve(double sx,double sy){
    double x=sx,y=sy,ans=getAns(sx,sy),step=1e6;
    while(step>eps){
        double sx=x,sy=y;
        bool flag=false;
        for(int i=0;i<8;i++){
            double dx=x+offx[i]*step,dy=y+offy[i]*step;
            double tmp=getAns(dx,dy);
            if(tmp>=INF) continue;
            if(tmp<ans){
                ans=tmp;
                flag=true;
                sx=dx,sy=dy;
            }
        }
        x=sx,y=sy;
        if(!flag) step/=2;
    }
    return ans;
}

void solve(){
    //cout<<tosolve(0,0)<<" "<<tosolve(sqrt(1.0/a),0)<<" "<<tosolve(0,sqrt(1.0/b))<<endl;
    double ans=tosolve(0,0),tmp;
    tmp=tosolve(sqrt(1.0/a),0);
    if(tmp<ans) ans=tmp;
    tmp=tosolve(-sqrt(1.0/a),0);
    if(tmp<ans) ans=tmp;
    tmp=tosolve(0,sqrt(1.0/b));
    if(tmp<ans) ans=tmp;
    tmp=tosolve(0,-sqrt(1.0/b));
    if(tmp<ans) ans=tmp;
    printf("%.7lf\n",ans);
}

int main(){
    while(scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f)!=EOF){
        solve();
    }
    return 0;
}

HDU 5017 Ellipsoid （计算几何，模拟退火）

标签：des   style   http   color   io   os   ar   for   strong   

原文地址：http://blog.csdn.net/a1061747415/article/details/39830299