标签:style blog http color io os 使用 ar for
A robot is located at the top-left corner of a m x n grid (marked ‘Start‘ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish‘ in the diagram below).
How many possible unique paths are there?
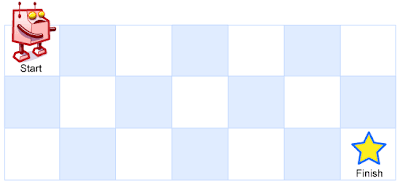
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
方法一:递归 f(m,n) = f(m-1, n) + f(m, n-1),m=1或n=1时,f(m,n) = 1
1 class Solution { 2 public: 3 int uniquePaths(int m, int n) { 4 if( m==1 || n==1 ) return 1; 5 return uniquePaths(m-1,n) + uniquePaths(m, n-1); 6 } 7 };
方法二:使用dp求解,dp[i][j] = dp[i-1][j] + dp[i][j-1], i = 1或j=1时,dp[i][j] = 1,代码可优化,便于理解不化~~
1 class Solution { 2 public: 3 int uniquePaths(int m, int n) { 4 vector< vector<int> > dp( m+1, vector<int>(n+1, 0) ); 5 for(int i=1; i<=m; ++i) dp[i][1] = 1; 6 for(int i=1; i<=n; ++i) dp[1][i] = 1; 7 for(int i=2; i<=m; ++i) 8 for(int j=2; j<=n; ++j) 9 dp[i][j] = dp[i-1][j] + dp[i][j-1]; 10 return dp[m][n]; 11 } 12 };
方法三:利用组合公式,格子走位问题,其实就是向下走m-1步,向右走n-1步,总共走m+n-2步,即在m+n-2步中挑选m-1步向下走,其余的步向右走
1 class Solution { 2 public: 3 int uniquePaths(int m, int n) { 4 return combination(m+n-2, m-1); 5 } 6 7 int combination(int n, int m) { 8 if( m > (n>>1) ) m = n-m; 9 long long ans = 1; 10 for(int i=1; i<=m; ++i) 11 ans = ans * (n-i+1) / i; //不能写成ans *= (n-i+1)/i; 12 return ans; 13 } 14 };
Follow up for "Unique Paths":
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.
[ [0,0,0], [0,1,0], [0,0,0] ]
The total number of unique paths is 2.
Note: m and n will be at most 100.
利用上题方法二,如果obstacle[i][j] = true,那么dp[i][j] = 0 否则 dp[i][j] = dp[i-1][j] + dp[i][j-1]
1 class Solution { 2 public: 3 int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid) { 4 int m = obstacleGrid.size(); 5 int n = obstacleGrid[0].size(); 6 if( m < 1 || n < 1 ) return 0; 7 vector< vector<int> > dp(m, vector<int>(n, 0)); 8 for(int i=0; i<n; ++i) //初始化很重要,若碰到一个障碍,那后面的都不能到达 9 if( !obstacleGrid[0][i] ) dp[0][i] = 1; 10 else break; 11 for(int i=0; i<m; ++i) 12 if( !obstacleGrid[i][0] ) dp[i][0] = 1; 13 else break; 14 for(int i=1; i<m; ++i) 15 for(int j=1; j<n; ++j) 16 if( !obstacleGrid[i][j] ) dp[i][j] = dp[i-1][j] + dp[i][j-1]; 17 return dp[m-1][n-1]; 18 } 19 };
标签:style blog http color io os 使用 ar for
原文地址:http://www.cnblogs.com/bugfly/p/4008586.html