标签:legend features more process eric eve finally span matrix
Matlab 环境:
1. 一元线性回归
ex1.m
%% Machine Learning Online Class - Exercise 1: Linear Regression
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% linear exercise. You will need to complete the following functions
% in this exericse:
%
% warmUpExercise.m
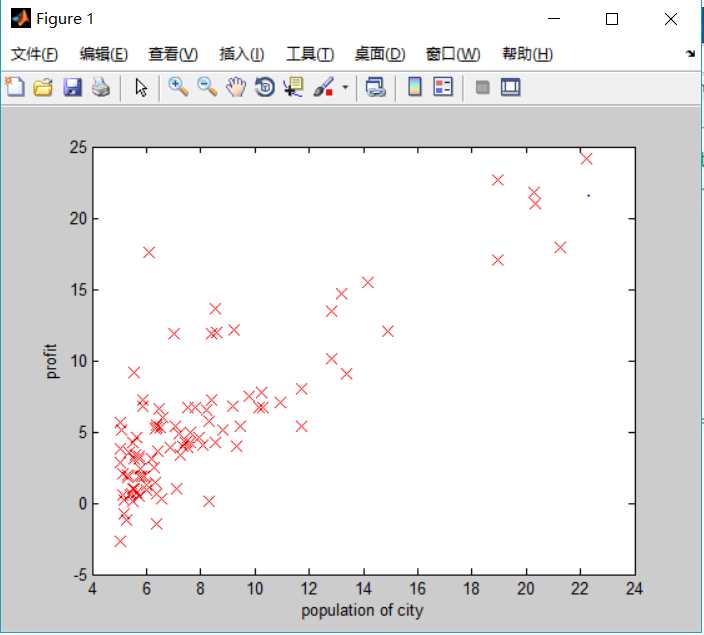
% plotData.m 绘制房屋面积和房屋价格的点状图
% gradientDescent.m 梯度下降法求theta
% computeCost.m 计算损失函数
% gradientDescentMulti.m
% computeCostMulti.m
% featureNormalize.m 特征缩放
% normalEqn.m 正规方程法求theta
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
% x refers to the population size in 10,000s
% y refers to the profit in $10,000s
%
%% Initialization
clear ; close all; clc
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf(‘Running warmUpExercise ... \n‘);
fprintf(‘5x5 Identity Matrix: \n‘);
warmUpExercise()
fprintf(‘Program paused. Press enter to continue.\n‘);
pause;
%% ======================= Part 2: Plotting =======================
fprintf(‘Plotting Data ...\n‘)
data = load(‘ex1data1.txt‘);
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf(‘Program paused. Press enter to continue.\n‘);
pause;
%% =================== Part 3: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf(‘\nTesting the cost function ...\n‘)
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf(‘With theta = [0 ; 0]\nCost computed = %f\n‘, J);
fprintf(‘Expected cost value (approx) 32.07\n‘);
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf(‘\nWith theta = [-1 ; 2]\nCost computed = %f\n‘, J);
fprintf(‘Expected cost value (approx) 54.24\n‘);
fprintf(‘Program paused. Press enter to continue.\n‘);
pause;
fprintf(‘\nRunning Gradient Descent ...\n‘)
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
% print theta to screen
fprintf(‘Theta found by gradient descent:\n‘);
fprintf(‘%f\n‘, theta);
fprintf(‘Expected theta values (approx)\n‘);
fprintf(‘ -3.6303\n 1.1664\n\n‘);
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, ‘-‘)
legend(‘Training data‘, ‘Linear regression‘)
hold off % don‘t overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf(‘For population = 35,000, we predict a profit of %f\n‘,...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf(‘For population = 70,000, we predict a profit of %f\n‘,...
predict2*10000);
fprintf(‘Program paused. Press enter to continue.\n‘);
pause;
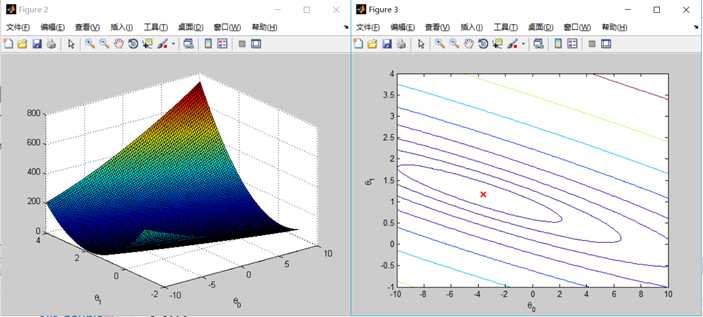
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf(‘Visualizing J(theta_0, theta_1) ...\n‘)
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0‘s
J_vals = zeros(length(theta0_vals), length(theta1_vals));
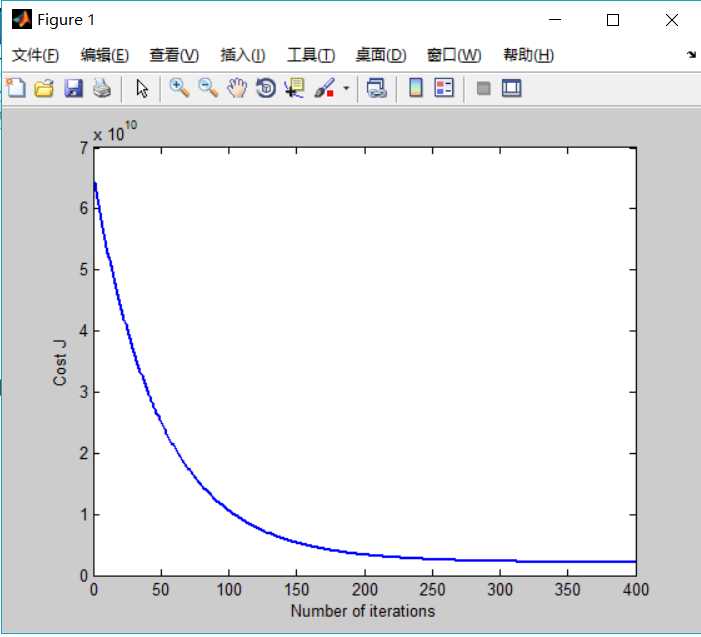
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals‘;
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);
hold on;
plot(theta(1), theta(2), ‘rx‘, ‘MarkerSize‘, 10, ‘LineWidth‘, 2);
computeCost.m
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
h = X * theta ; % cal the hypothesis
J = 1/(2*m) * sum((h-y) .^ 2 ) ;
% =========================================================================
end
gradientDescent.m
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
h = X * theta ;
h_minus = h - y;
h_sum = ( h_minus‘ * X )‘;
theta = theta - alpha * h_sum ./ m;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
多元线性回归
ex1_multi.m
1 %% Machine Learning Online Class 2 % Exercise 1: Linear regression with multiple variables 3 % 4 % Instructions 5 % ------------ 6 % 7 % This file contains code that helps you get started on the 8 % linear regression exercise. 9 % 10 % You will need to complete the following functions in this 11 % exericse: 12 % 13 % warmUpExercise.m 14 % plotData.m 15 % gradientDescent.m 16 % computeCost.m 17 % gradientDescentMulti.m 18 % computeCostMulti.m 19 % featureNormalize.m 20 % normalEqn.m 21 % 22 % For this part of the exercise, you will need to change some 23 % parts of the code below for various experiments (e.g., changing 24 % learning rates). 25 % 26 27 %% Initialization 28 29 %% ================ Part 1: Feature Normalization ================ 30 31 %% Clear and Close Figures 32 clear ; close all; clc 33 34 fprintf(‘Loading data ...\n‘); 35 36 %% Load Data 37 data = load(‘ex1data2.txt‘); 38 X = data(:, 1:2); 39 y = data(:, 3); 40 m = length(y); 41 42 % Print out some data points 43 fprintf(‘First 10 examples from the dataset: \n‘); 44 fprintf(‘ x = [%.0f %.0f], y = %.0f \n‘, [X(1:10,:) y(1:10,:)]‘); 45 46 fprintf(‘Program paused. Press enter to continue.\n‘); 47 pause; 48 49 % Scale features and set them to zero mean 50 fprintf(‘Normalizing Features ...\n‘); 51 52 [X mu sigma] = featureNormalize(X); 53 54 % Add intercept term to X 55 X = [ones(m, 1) X]; 56 57 58 %% ================ Part 2: Gradient Descent ================ 59 60 % ====================== YOUR CODE HERE ====================== 61 % Instructions: We have provided you with the following starter 62 % code that runs gradient descent with a particular 63 % learning rate (alpha). 64 % 65 % Your task is to first make sure that your functions - 66 % computeCost and gradientDescent already work with 67 % this starter code and support multiple variables. 68 % 69 % After that, try running gradient descent with 70 % different values of alpha and see which one gives 71 % you the best result. 72 % 73 % Finally, you should complete the code at the end 74 % to predict the price of a 1650 sq-ft, 3 br house. 75 % 76 % Hint: By using the ‘hold on‘ command, you can plot multiple 77 % graphs on the same figure. 78 % 79 % Hint: At prediction, make sure you do the same feature normalization. 80 % 81 82 fprintf(‘Running gradient descent ...\n‘); 83 84 % Choose some alpha value 85 alpha = 0.01; 86 num_iters = 400; 87 88 % Init Theta and Run Gradient Descent 89 theta = zeros(3, 1); 90 [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters); 91 92 % Plot the convergence graph 93 figure; 94 plot(1:numel(J_history), J_history, ‘-b‘, ‘LineWidth‘, 2); 95 xlabel(‘Number of iterations‘); 96 ylabel(‘Cost J‘); 97 98 % Display gradient descent‘s result 99 fprintf(‘Theta computed from gradient descent: \n‘); 100 fprintf(‘ %f \n‘, theta); 101 fprintf(‘\n‘); 102 103 % Estimate the price of a 1650 sq-ft, 3 br house 104 % ====================== YOUR CODE HERE ====================== 105 % Recall that the first column of X is all-ones. Thus, it does 106 % not need to be normalized. 107 price = 0; % You should change this 108 X_1 = [1 1650 3] ; 109 price = X_1 * theta ; 110 % ============================================================ 111 112 fprintf([‘Predicted price of a 1650 sq-ft, 3 br house ‘ ... 113 ‘(using gradient descent):\n $%f\n‘], price); 114 115 fprintf(‘Program paused. Press enter to continue.\n‘); 116 pause; 117 118 %% ================ Part 3: Normal Equations ================ 119 120 fprintf(‘Solving with normal equations...\n‘); 121 122 % ====================== YOUR CODE HERE ====================== 123 % Instructions: The following code computes the closed form 124 % solution for linear regression using the normal 125 % equations. You should complete the code in 126 % normalEqn.m 127 % 128 % After doing so, you should complete this code 129 % to predict the price of a 1650 sq-ft, 3 br house. 130 % 131 132 %% Load Data 133 data = csvread(‘ex1data2.txt‘); 134 X = data(:, 1:2); 135 y = data(:, 3); 136 m = length(y); 137 138 % Add intercept term to X 139 X = [ones(m, 1) X]; 140 141 % Calculate the parameters from the normal equation 142 theta = normalEqn(X, y); 143 144 % Display normal equation‘s result 145 fprintf(‘Theta computed from the normal equations: \n‘); 146 fprintf(‘ %f \n‘, theta); 147 fprintf(‘\n‘); 148 149 150 % Estimate the price of a 1650 sq-ft, 3 br house 151 % ====================== YOUR CODE HERE ====================== 152 price = 0; % You should change this 153 X_2 = [ 1 1650 3] ; 154 price = X_2 * theta ; 155 % ============================================================ 156 157 fprintf([‘Predicted price of a 1650 sq-ft, 3 br house ‘ ... 158 ‘(using normal equations):\n $%f\n‘], price);
特征缩放
1 function [X_norm, mu, sigma] = featureNormalize(X) 2 %FEATURENORMALIZE Normalizes the features in X 3 % FEATURENORMALIZE(X) returns a normalized version of X where 4 % the mean value of each feature is 0 and the standard deviation 5 % is 1. This is often a good preprocessing step to do when 6 % working with learning algorithms. 7 8 % You need to set these values correctly 9 X_norm = X; 10 mu = zeros(1, size(X, 2)); 11 sigma = zeros(1, size(X, 2)); 12 13 % ====================== YOUR CODE HERE ====================== 14 % Instructions: First, for each feature dimension, compute the mean 15 % of the feature and subtract it from the dataset, 16 % storing the mean value in mu. Next, compute the 17 % standard deviation of each feature and divide 18 % each feature by it‘s standard deviation, storing 19 % the standard deviation in sigma. 20 % 21 % Note that X is a matrix where each column is a 22 % feature and each row is an example. You need 23 % to perform the normalization separately for 24 % each feature. 25 % 26 % Hint: You might find the ‘mean‘ and ‘std‘ functions useful. 27 % 28 mu = mean(X); % 1 * ( n + 1 ) 29 sigma = std(X); 30 for i = 1 : size(X,1) 31 X_norm(i,:) = ( X_norm(i,:) - mu ) ./ sigma ; % 对每个行向量做减法 32 end 33 % X_norm(1:10,:) 34 35 % ============================================================ 36 37 end
computeCostMulti and gradientDescent是没有变的。
正规方程法
1 function [theta] = normalEqn(X, y) 2 %NORMALEQN Computes the closed-form solution to linear regression 3 % NORMALEQN(X,y) computes the closed-form solution to linear 4 % regression using the normal equations. 5 6 theta = zeros(size(X, 2), 1); 7 8 % ====================== YOUR CODE HERE ====================== 9 % Instructions: Complete the code to compute the closed form solution 10 % to linear regression and put the result in theta. 11 % 12 13 % ---------------------- Sample Solution ---------------------- 14 15 theta = pinv(X‘*X)*X‘*y; 16 17 18 % ------------------------------------------------------------- 19 20 21 % ============================================================ 22 23 end
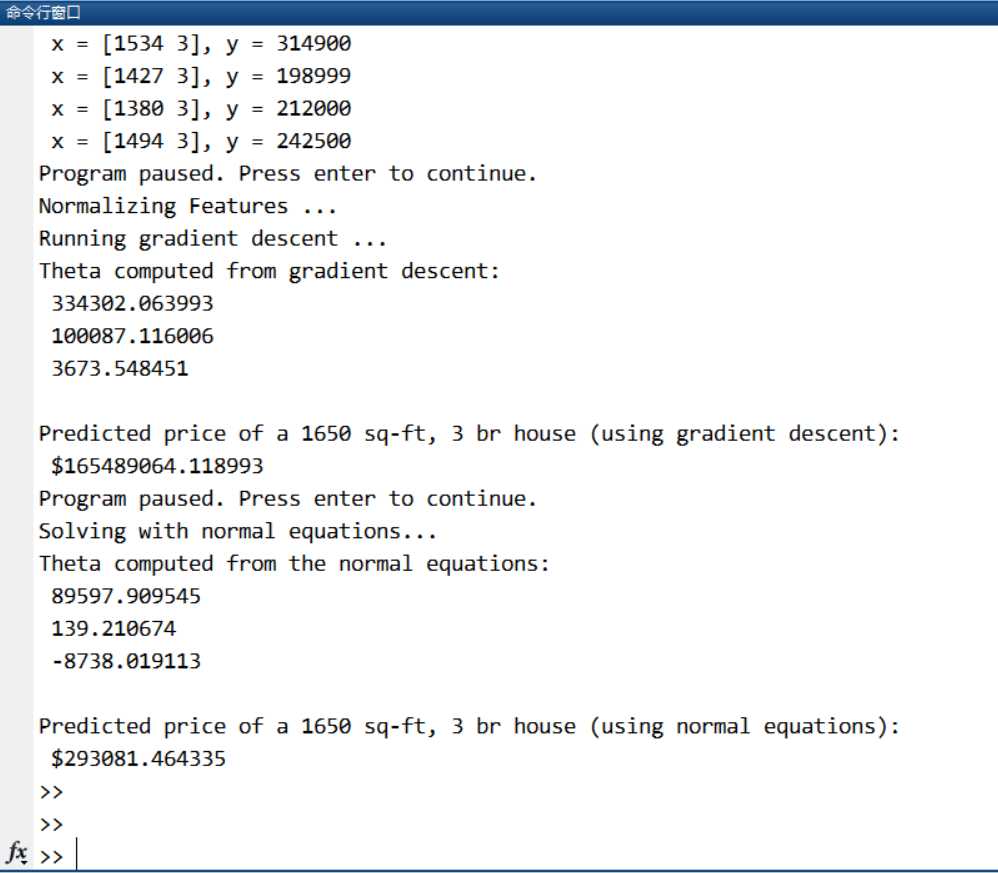
coursera 机器学习 linear regression 线性回归的小项目
标签:legend features more process eric eve finally span matrix
原文地址:https://www.cnblogs.com/twomeng/p/9531167.html