标签:解释 取数 ali lin 基于 训练 判断 过程 调整
全文引用自《统计学习方法》(李航)
感知机(perceptron) 最早由Rosenblatt于1957年提出,是一种较为简单的二分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,类别取值为+1或-1。感知机的训练目标是训练出一个超平面,能够将训练数据进行线性划分。因此,确定一个基于误分类的损失函数,并利用梯度下降法等优化方法对损失函数进行极小化训练,最终可以得出一个可用的感知机模型。感知机学习算法非常简单且易于实现,是实现神经网络和支持向量机模型的基础。
本篇文章通过介绍感知机的模型、学习策略和学习算法三要素,来具体介绍感知机算法。
感知机需要学习一个线性模型,能够对输入的特征向量,输出具体的分类属性。因此其模型由输入空间向输出空间的映射函数应为:
\[
f(x)=sign(w\cdot x+b)
\]
此模型即为感知机模型。其中,输入空间(特征空间)为\(X\subseteq R^n\),输出空间为\(Y=\{+1,-1\}\)。其中,输入\(x\in X\)表示实例的特征向量,输出\(y\in Y\)表示实例的类别。\(w\in R^n\)和\(b\in R\)为感知机模型的参数,前者叫权值(weight),后者叫偏置(bias),\(w\cdot x\)表示两者的内积,sign()是符号函数,具体为:
\[
sign(x)=\begin{cases}
+1, x\geq 0\-1, x< 0\\end{cases}
\]
感知机是一种线性分类模型,其假设空间是输入的特征空间中所有的线性分类模型,即\(\{f|f(x)=w\cdot x+b\}\)。
对于感知机的理解,可以通过二维平面内的线性分类例子作类比。
感知机的线性方程:
\[w\cdot x+b=0\]
对应于特征空间\(R^n\)内的一个超平面\(S\),其中,\(w\)是超平面的法向量,\(b\)是超平面的截距。此超平面将特征空间分为两个部分,即将空间中的实例分为正负两类。此时,称超平\(S\)为分离超平面(separating hyperplane)。
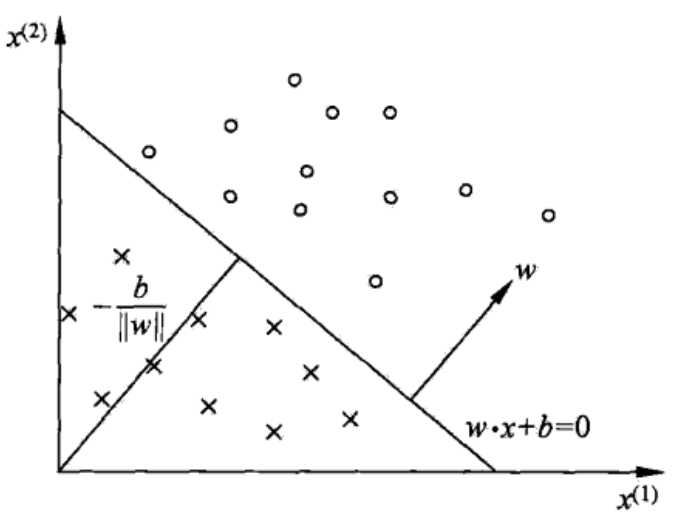
对感知机模型的训练,就是求取合适的\(w\)和\(b\),得到最终的分离超平面,最后对新的输入进行分类。
感知机是二维线性分类器,因此使用的前提条件是,输入数据集的线性可分。
线性可分(linearly separable) 的定义为:
给定一个数据集
\[
T=\{(x_1,y_1),(x_2,y_2),...,(x_{_N},y_{_N})\},
\]
其中\(x_i\in X=R^n, y_i\in Y=\{+1,-1\}, i=1,2,...,N\),若存在某个超平面S:
\[
w\cdot x+b=0
\]
能够将数据集的正负实例完全正确的分成两个部分,则称数据集T是线性可分的,否则称T线性不可分。
假定训练数据集是线性可分的,那么感知机要学习模型参数\(w,b\)便需要确定一个学习策略,即定义一个模型的经验损失函数,并对损失函数进行最优化(极小化)训练。
在感知机模型中,通常选择利用所有误分类点到超平面S之间的距离总和来表示模型的损失。
在输入空间\(R^n\)中,任意一点\(x_0\)到超平面S之间的距离为:
\[
\frac{1}{\|w\|}|w\cdot x_0+b|
\]
其中,\(\|w\|\)是\(w\)的\(L_2\)范数。
对于误分类的数据\((x_i,y_i)\)来说,
\[
-y_i(w\cdot x_i +b)>0
\]
始终成立,因为点\((x_i,y_i)\)为误分类点,所以当\(w\cdot x+b>0\)时,\(y_i = -1\),当\(w\cdot x+b<0\)时,\(y_i = +1\),因此,误分类点\(x_i\)到超平面S的距离为
\[
-\frac{1}{\|w\|}y_i(w\cdot x_i+b)
\]
那么对于所有的误分类点到超平面S的距离总和为:
\[
-\frac{1}{\|w\|}\sum_{x_i\in M}y_i(w\cdot x_i+b)
\]
因为距离总和始终为正,且对分类结果对错的判断只与符号相关,因此为方便,不考虑\(\frac{1}{\|w\|}\),则可得到感知机的损失函数。
给定的训练数据集为:
\[
T=\{(x_1,y_1),(x_2,y_2),...,(x_{_N},y_{_N})\},
\]
其中\(x_i\in X=R^n, y_i\in Y=\{+1,-1\}, i=1,2,...,N\),则感知机\(sign(w\cdot x+b)\)学习的损失函数为:
\[
L(w,b)=-\sum_{x_i\in M}{y_i(w\cdot x_i +b)}
\]
其中,M为误分类点的集合。此函数即为感知机的经验风险函数。
由上述可知,损失函数\(L(w,b)\)是非负的,若没有误分类点,则其值为0。且误分类点越少,或误分类点距离超平面越近,损失函数的值就越小。
对于一个特定的样本点的损失函数,其在误分类时,是\(w,b\)的线性函数,在正确分类时为0。因此,在给定的训练数据集T上,损失函数是\(w,b\)的连续可导函数。
综上,感知机的学习策略就是在特征空间的所有感知机模型中,选择能够使损失函数\(L(w,b)\)值最小的\(w,b\)参数的模型,即最优的模型。
感知机学习的过程就是求解损失函数的最优化问题的过程,而最优化方法通常采用随机梯度下降法。
感知机学习算法是针对以下最优化问题的算法:
给定一个训练数据集为:
\[
T=\{(x_1,y_1),(x_2,y_2),...,(x_{_N},y_{_N})\}
\]
其中\(x_i\in X=R^n, y_i\in Y=\{+1,-1\}, i=1,2,...,N\),求解参数\(w,b\),其为极小化损失函数的解:
\[
\min_{w,b}L(w,b)=-\sum_{x_i\in M}{y_i(w\cdot x_i +b)}
\]
其中M为误分类点。
首先,算法选择一个初始的超平面\(w_0,b_0\),然后利用梯度下降法不断极小化目标函数。在极小化的过程中,我们不是一次使用M中所有的误分类点进行梯度下降,而是随机选择一个误分类点进行参数的更新。
假定误分类点的集合M是固定的,那么损失函数\(L(w,b)\)的梯度为:
\[
\begin{align}
\nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i\\nabla_bL(w,b)=-\sum_{x_i\in M}y_i\\end{align}
\]
那么随机选择一个误分类点\((x_i,y_i)\),对\(w,b\)进行更新:
\[
\begin{align}
w‘=w-\eta\nabla_wL(w,b)=w+\eta y_ix_i\b‘=b-\eta\nabla_bL(w,b)=b+\eta y_i\\end{align}
\]
其中\(\eta(0<\eta\leq1)\)是参数更新的步长,又称为学习率(learning rate)。通过以上步骤,不断地利用误分类点进行迭代,使\(L(w,b)\)不断减小,直到0。
综上,感知机学习算法的原始形式为:
对算法最为直观的解释为:当一个实例点被误分类时,处于超平面的错误的一侧。此时,调整\(w,b\)的值,使超平面向误分类点移动,以减少与误分类点之间的距离,直至误分类点处于超平面的另一侧,此时实例点被正确分类。
假定对于一个实例点\((x_i,y_i)\),算法通过
\[
\begin{align}
w\leftarrow w+\eta y_ix_i\b\leftarrow b+\eta y_i\\end{align}
\]
进行不断的更新,总计对\(w,b\)修改了\(n_i\)次,若\(w,b\)初始值均为0,此时可以得出:
\[
\begin{align}
w=\sum_{i=1}^{N}n_i\eta y_ix_i\b=\sum_{i=1}^{N}n_i\eta y_i\\end{align}
\]
当\(n_i\)越大时,我们可以认为该实例点对参数进行更新的次数更多,即其被误分类的次数更多,那么就意味着它更接近超平面,因为只有接近超平面的点,在超平面稍微移动时,才会有很大的分类差别。此时意味着这个点就越难以进行分类,它对学习结果的影响也就最大。
将上述公式带入感知机算法的原始形式可得感知机模型为:
\[
f(x)=sign(w\cdot x+b)=sign(\sum_{j=1}^{N}n_j\eta y_jx_j\cdot x+\sum_{j=1}^{N}n_j\eta y_j)
\]
此时,学习的目标不再是求出\(w,b\),而是求出\(n_i,i=1,2,\cdots,N\)。
综上,感知机学习算法的对偶形式为:
由此可以看出,感知机学习算法的对偶形式与原始形式并没有本质的区别,那其意义是什么?
在对偶形式的训练中,我们可以看出,训练的实例仅仅以内积的形式出现,我们实际训练的是\(n_i\),当训练数据的维度很高时,使用感知机学习算法的原始形式,会需要极大的计算量,因为每一次更新都需要计算\(x_i\)和\(w\)的内积。而采用对偶形式,可以提前算出实例之间的所有内积,并以矩阵的形式存储下来,即所谓的Gram矩阵
\[
G=[x_i,x_j]_{_{N\times N}}
\]
这样,在进行训练时,就可以直接从矩阵中取出所需值,可以极大降低算法的复杂度。
标签:解释 取数 ali lin 基于 训练 判断 过程 调整
原文地址:https://www.cnblogs.com/zhiyuxuan/p/9531114.html