『8.24 模拟赛』豪迈

标签：src   inf   bre   .com   一个   register   sort   事物   continue   

题目链接戳这里n(*≧▽≦*)n

题目描述

ranwen特别喜欢数列和树，他觉得它们是世界上最美妙的事物。

有一天， 某人给了ranwen一个长度为N的整数数列a。这让ranwen特别想构造一棵豪迈树。

豪迈树的每条边长度都为1。而且豪迈树有一个最重要的性质：对于每一个点i（1<=i<=N），在树中离它距离最远的点与它的距离应恰好等于ai。

ranwen想了想就秒掉了这题，他决定考考你：对于一个给定的序列，是否存在一棵豪迈树？

解题思路

挺简单的一道题，我们首先对最长距离排好序，最长的那个就是树的直径。

我们就可以先画一条链，像下面这条：

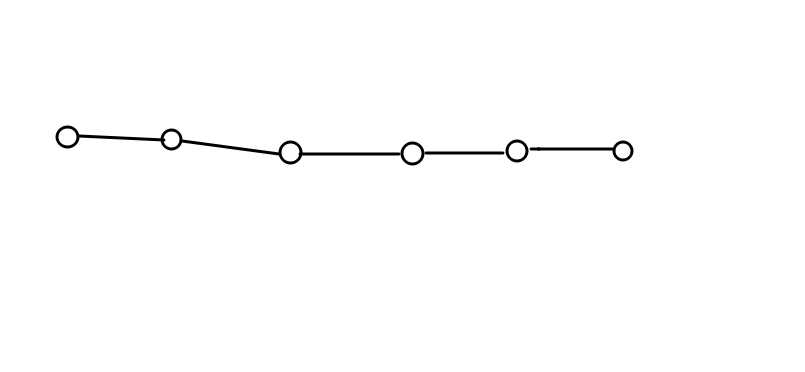
那么显然，这样长度为5,4,3的点各有两个，那么更多的点如何构造呢？

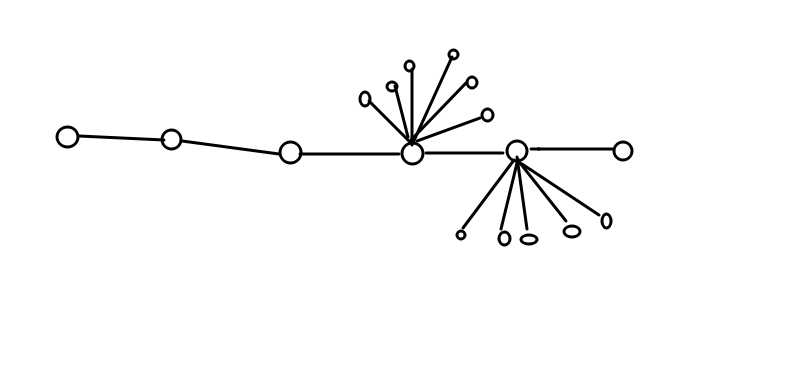
像这样，我们在每个点上开花一样的开出点，就可以得到任意数量的长度在\(\lceil\)\(\frac{a_{max}}{2}\)\(\rceil\)到\(a_{max}\)之间的点的个数，那么解题方法就很明确了：

1）对于\(a_{max}\)为奇数的情况：\(\lceil\)\(\frac{a_{max}}{2}\)\(\rceil\)到\(a_{max}\)之间每个长度至少有两个点。

2）对于\(a_{max}\)为偶数的情况：\(\frac{a_{max}}{2}\)只能有一个点，剩下的每个长度至少有两个点。

附上代码：

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=100500;
int T,n;
int a[maxn],flag[maxn];
int main(){
    scanf("%d",&T);
    for(register int t=1;t<=T;t++){
        memset(flag,0,sizeof(flag));
        scanf("%d",&n);
        for(register int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            flag[a[i]]++;
        }
        sort(a+1,a+n+1);
        int tmp=(a[n]>>1)+(a[n]&1);
        if(a[n]!=a[n-1]||tmp>a[1]){
            cout<<"Impossible"<<endl;
            continue;
        }
        if(a[n]&1){
            if(flag[tmp]>2){
                cout<<"Impossible"<<endl;
                continue;
            }
            int fl=0;
            for(register int i=tmp+1;i<=a[n];i++){
                if(a[i]<2){
                    fl=1;
                    break;
                }
            }
            if(fl){
                cout<<"Impossible"<<endl;
                continue;
            }
            else cout<<"Possible"<<endl;
            continue;
        }
        else {
            if(flag[tmp]>1){
                cout<<"Impossible"<<endl;
                continue;
            }
            int fl=0;
            for(register int i=tmp+1;i<=a[n];i++){
                if(a[i]<2){
                    fl=1;
                    break;
                }
            }
            if(fl){
                cout<<"Impossible"<<endl;
                continue;
            }
            else cout<<"Possible"<<endl;
            continue;
        }
    }
}

『8.24 模拟赛』豪迈

标签：src   inf   bre   .com   一个   register   sort   事物   continue   

原文地址：https://www.cnblogs.com/Fang-Hao/p/9531781.html