标签:分类 nump 训练 code png 提前 display com 多个
如果输入是一个n维向量\(x∈\mathbb{R}^n\),输出为样本的类别{+1,-1}。由输入到输出有以下函数:\[f(x)=sign(\omega·x+b)\] 则称该函数为感知机。其中\(\omega\)和\(b\)为感知机参数,\(\omega\)被称为权值(weight)或者权值向量(weight vector),\(b\)被称为偏置(bias),\(\omega · x\)为点乘(对应元素相乘后相加,结果为一个标量),sign为符号函数,定义为:
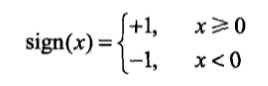
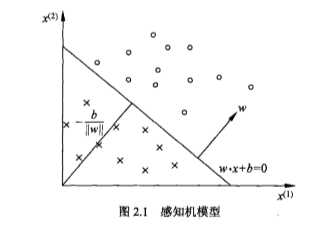
如果对于训练数据集:\[T={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)}\]其中\(x_i\)为n维向量,\(y_i∈\{+1,-1\}\),存在某个超平面\(S\),使得\[\omega·x+b=0\] 能够将数据集的正实例点和负实例点正确地划分到平面两侧,也就是说对于所有\(y_i=1\)的实例i,有\(\omega·x_i+b>0\),对于所有\(y_j=-1\)的实例j,有\(\omega·x+b<0\),那么我们称数据集T为线性可分数据集,否则称数据集T不可分。
假设训练数据集是线性可分的,那么感知机学习的目标就是找出一个超平面(确定\(\omega,b\)的值)将正实例点和负实例点完全正确分开。为了找出这样的超平面,我们需要一个学习策略来定义损失函数并将损失函数最小化。
损失函数的一个自然选择是误分类点的个数,但这样的损失函数不是\(\omega,b\)的连续可导函数,不易优化。损失函数的另一个选择是误分类点到超平面S的距离之和,这是感知机采用的。首先输入空间任一点\(x∈\mathbb{R}^n\)到超平面\(S\)的距离为:
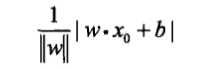
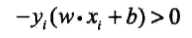
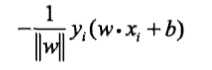
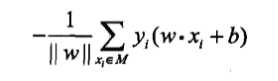
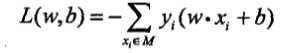
在上一节中,我们已经求得了损失函数的形式,感知机的学习问题就转换为了损失函数的最优化问题(找到合适的\(\omega,b\)使得超平面\(S\)能正确分类),在本节最优化使用的方法是随机梯度下降法。感知机学习算法分为两类:原始形式和对偶形式,两种算法在训练数据集\(T\)线性可分时均收敛(也就是经过算法的有限次迭代可以找到一个将训练数据集完全正确分开的超平面的感知机模型)。
感知学习算法是对损失函数最优化的算法,也就是找出\(\omega,b\)使得损失函数取最小值,用公式表示就是:
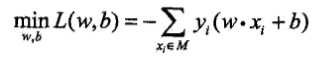
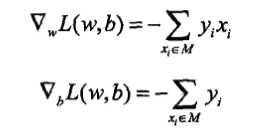
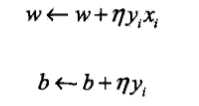
输入:
1、线性可分数据集\(T={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)}\)其中\(x_i\)为n维向量,\(y_i∈\{+1,-1\}\)
2、学习率\(\eta\)
输出:
1、\(\omega,b\)
2、感知机模型\(f(x)=sign(\omega·x+b)\)
步骤:
(1)选取初值\(\omega,b\)
(2)在训练集中选取数据\((x_i,y_i)\)
(3)如果\(y_i(\omega·x+b)≤0\)(该点被误分类),那么更新\(\omega,b\)的值:
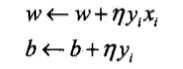
假设正实例点有\(x_1=(3,3)^T,x_2=(4,3)^T\),负实例点有\(x_3=(1,1)^T\),令\(\eta=1\),则求权值向量\(\omega=(\omega_1,\omega_2)^T\)和\(b\)以及感知机学习模型\(f(x)=sign(\omega·x)+b\)。
求解步骤如下:
(1)令初值\(\omega=b=0\)
(2)对于\(x_1=(3,3)^T\),\(y_1(\omega·x_1+b)=0≤0\),\(x_1\)未能被正确分类,所以更新\(\omega,b\)的值:
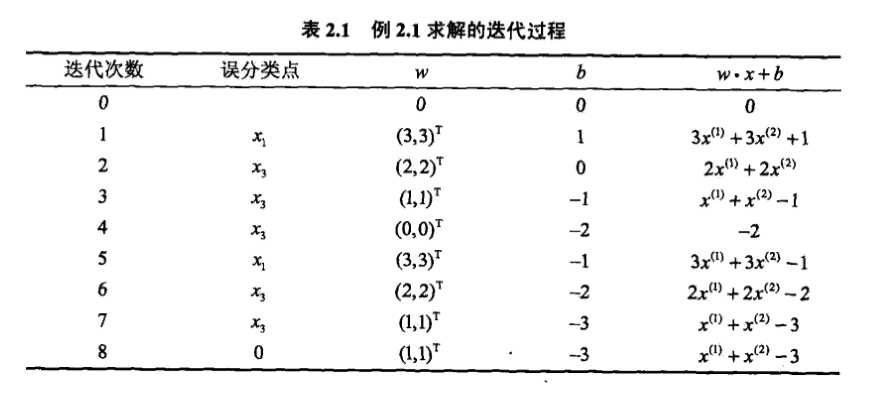
使用python将上面的例子实现,代码如下:
import numpy as np
x = np.array([[3,3], [4,3], [1,1]])
y = [1, 1, -1]
def init():
eta = 1
w = np.array([0, 0])
b = 0
return eta, w, b
def perceptron():
eta, w, b = init()
i = 0
while i<len(x):
if y[i]*(np.dot(w,x[i])+b) <= 0:
w = w + eta * y[i] * x[i]
b = b + eta * y[i]
print u"x{}被误分类,更新后w={},b={}".format(i+1,w,b)
i = 0 #有误分类点,重新遍历
else:
i += 1
perceptron()输出:
x1被误分类,更新后w=[3 3],b=1
x3被误分类,更新后w=[2 2],b=0
x3被误分类,更新后w=[1 1],b=-1
x3被误分类,更新后w=[0 0],b=-2
x1被误分类,更新后w=[3 3],b=-1
x3被误分类,更新后w=[2 2],b=-2
x3被误分类,更新后w=[1 1],b=-3当感知学习算法采用不同的初值时,最终的解可以不同(解不止一个)。
对偶形式与原始形式的区别在于判断点是否被正确分类的方法以及更新\(\omega,b\)的方法。
输入:
1、线性可分数据集\(T={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)}\)其中\(x_i\)为n维向量,\(y_i∈\{+1,-1\}\)
2、学习率\(\eta\)
输出:
1、\(\alpha,b\),其中\(\alpha=(\alpha_1,\alpha_2,...,\alpha_n)^T\),是一个n维向量
2、感知机模型\(f(x)=sign(\sum_{j=1}^N\alpha_jy_jx_j·x+b)\)
步骤:
(1)令初值\(\alpha=b=0\)
(2)在训练集选取数据\((x_i, y_i)\)
(3)如果\(y_i(\sum_{j=1}^N\alpha_jy_jx_j·x_i+b)≤0\),则更新\(\alpha,b\):
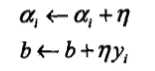
数据和上一个例子相同:正实例点有\(x_1=(3,3)^T,x_2=(4,3)^T\),负实例点有\(x_3=(1,1)^T\),用感知机算法对偶形式求感知机模型。
求解步骤如下:
(1)取\(\alpha_i=0,i=1,2,3, b=0, \eta=1\)
(2)计算Gram矩阵:
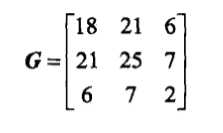
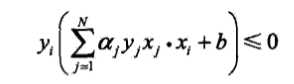
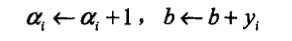
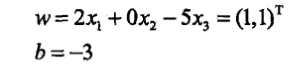
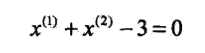
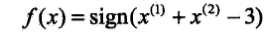
将上面的步骤使用python实现,代码如下:
import numpy as np
x = np.array([[3,3], [4,3], [1,1]])
y = [1, 1, -1]
g = np.zeros([3, 3])
# 计算gram矩阵
def gram():
for i in range(len(x)):
for j in range(len(x)):
g[i,j] = np.dot(x[i], x[j])
def init():
gram()
eta = 1
alpha = np.zeros([1, 3], dtype=int).flatten()
b = 0
return eta, alpha, b
# 得到损失函数的前半部分求和
def get_sum(alpha, xi):
s = 0
for j in range(3):
s += np.dot(alpha[j]*y[j]*x[j], xi)
return s
def perceptron():
eta, alpha, b = init()
i = 0
while i<len(x):
if y[i]*(get_sum(alpha, x[i])+b) <= 0:
alpha[i] += 1
b += y[i]
print "x{}被误分类,更新后alpha={},b={}".format(i+1,alpha,b)
i = 0
else:
i += 1
perceptron()输出:
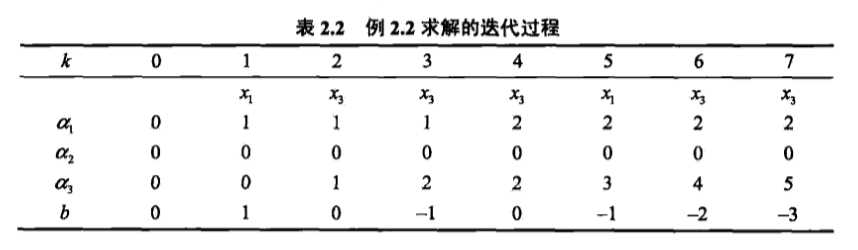
x1被误分类,更新后alpha=[1 0 0],b=1
x3被误分类,更新后alpha=[1 0 1],b=0
x3被误分类,更新后alpha=[1 0 2],b=-1
x3被误分类,更新后alpha=[1 0 3],b=-2
x1被误分类,更新后alpha=[2 0 3],b=-1
x3被误分类,更新后alpha=[2 0 4],b=-2
x3被误分类,更新后alpha=[2 0 5],b=-31、感知机是根据数据的特征向量对其进行二类分类(+1,-1)的线性分类模型:\[f(x)=\omega·x+b\] 感知机模型在集合上对应输入空间的分离超平面\[\omega·x+b=0\]
2、感知机学习的策略是极小化损失函数:
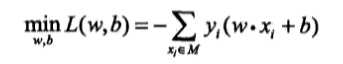
1、李航《统计学习方法》
标签:分类 nump 训练 code png 提前 display com 多个
原文地址:https://www.cnblogs.com/sench/p/9530250.html