从一个题目的解答过程看数学知识的积累的重要性

已知命题\(p\)：\(\exists x_0\in R\)，\(e^{x_0}-mx_0=0\)，命题\(q\)：\(\forall x\in R\)，\(x^2+mx+1\ge 0\)，若\(p\lor(\neg q)\)为假命题，求实数\(m\)的取值范围。

【解析】由复合命题真值表可知，\(p\lor(\neg q)\)为假命题，

则\(p\)和\(\neg q\)都为假命题，即\(p\)假\(q\)真。

先说命题\(q\)：\(\forall x\in R\)，\(x^2+mx+1\ge 0\)，为真命题，则属于恒成立命题，

则\(\Delta=m^2-4\leq 0\)，解得\(-2\leq m\leq 2\)；以下重点研究命题\(p\)。

而由题目可知，\(\neg p\)：\(\forall x\in R\)，\(e^x-mx \neq 0\)，为真命题。

即方程\(e^x-mx \neq 0\)无实根，此时准备分离参数：

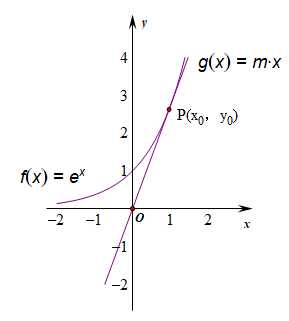
思路一：不完全分离参数得到，方程\(mx= e^x\) 无实根，

即函数\(y=e^x\)和函数\(y=mx\)的图像没有交点。做出辅助图像如右所示，

设直线\(y=mx\)与曲线\(y=e^x\)相切于点\(P(x_0，y_0)\)，

则\(\left\{\begin{array}{l}{m=e^{x_0}①}\\{y_0=e^{x_0}②}\\{y_0=mx_0③}\end{array}\right.\)

(上述方程的来源是：从斜率相等角度，从切点在曲线上的角度，从切点在直线上的角度)

解得切点坐标为\(P(1，e)\)，\(m=e\)，即二者相切时的斜率为\(e\)，

故由图可知，两个函数图像没有交点时，\(0\leq m<e\)。

思路二：完全分离参数得到，方程\(m=\cfrac{e^x}{x}\)无实根，