2018.2.23 省选模拟赛

时间：2018-08-25 17:33:20 阅读：187 评论：0 收藏：0 [点我收藏+]

标签：dep 负数奇数 line split 过多 tle span signed

从这里开始

Problem A cycle
Problem B meal
Problem C naive

Problem A cycle

技术分享图片

　　判断是否有经过一个点的负环，我们可以跑最短路。判断这个点到自己的最短路是否是负数。

　　于是可以二分环大小跑dfs版spfa。

　　于是可以分层图做时间复杂度四方的dp。

　　（YYR给的数据水得吓人，这两个做法居然都跑过了。然后都被我和jmr卡掉了）

　　注意到如果一个点走不超过$k$条边回到自己的最短路的长度是负数，那么走不超过$k + 1$条边也是。

　　因此我们可以二分答案，然后用快速幂算Floyd。时间复杂度$O(n^{3}\log^{2}n)$，成功爆炸。

　　但是考虑先预处理走$2^i$步的矩阵，然后倍增。

　　这样时间复杂度降为$O(n^{3}\log n)$。

Code

 1 #include <iostream>
 2 #include <cstdlib>
 3 #include <cstdio>
 4 #include <ctime>
 5 using namespace std;
 6 typedef bool boolean;
 7 
 8 const int N = 305;
 9 const signed int inf = (signed) (~0u >> 2);
10 
11 int n, m;
12 
13 typedef class Matrix {
14     public:
15         int ar[N][N];
16 
17         int* operator [] (int p) {
18             return ar[p];
19         }
20 
21         Matrix operator * (Matrix br) {
22             Matrix rt;
23             for (int i = 0; i < n; i++)
24                 for (int j = 0; j < n; j++)
25                     rt[i][j] = ((i == j) ? (0) : (inf));        
26             for (int i = 0; i < n; i++)
27                 for (int k = 0; k < n; k++)
28                     for (int j = 0; j < n; j++)
29                         rt[i][j] = min(rt[i][j], ar[i][k] + br[k][j]);
30             return rt;
31         }
32 }Matrix;
33 
34 const int bzmax = 10;
35 
36 Matrix g, f;
37 Matrix pws[bzmax + 1];
38 
39 inline void init() {
40     scanf("%d%d", &n, &m);
41     for (int i = 0; i < n; i++)
42         for (int j = 0; j < n; j++)
43             g[i][j] = ((i == j) ? (0) : (inf));    
44     for (int i = 1, u, v, w; i <= m; i++) {
45         scanf("%d%d%d", &u, &v, &w);
46         u--, v--;
47         g[u][v] = w;
48     }
49 }
50 
51 inline void solve() {
52     pws[0] = g;
53     for (int i = 1; i < bzmax; i++)
54         pws[i] = pws[i - 1] * pws[i - 1];
55     int res = 1;
56     for (int i = bzmax - 1; ~i; i--) {
57         if (res + (1 << i) > n)
58             continue;
59         f = g * pws[i];
60         boolean aflag = false;
61         for (int u = 0; u < n && !aflag; u++)
62             if (f[u][u] < 0)
63                 aflag = true;
64         if (!aflag)
65             res = (res + (1 << i)), g = f;
66     }
67     if (res >= n)
68         puts("0");
69     else
70         printf("%d\n", res + 1);
71 }
72 
73 int main() {
74     freopen("cycle.in", "r", stdin);
75     freopen("cycle.out", "w", stdout);
76     init();
77     solve();
78     return 0;
79 }

Problem A

Problem B meal

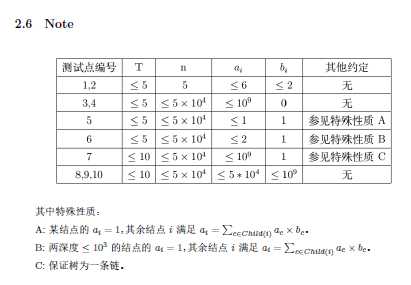
技术分享图片

　　设$num_{i} = a_{i} - \sum_{c \in Child(i)}a_{c}b_{c}$。

　　然后这个问题可以看成树上每个节点有$num_{i}$堆石子，每取走节点$i$的$k$颗石子，就会在它的父节点处放入$k \times b_{i}$颗石子。

　　对于深度为偶数点无论取多少石子放入父节点意义都不大，因为下一个人可以把它们都重新移入深度为偶数的点。

　　对于操作一个深度为奇数的点上的石子，会把它移到深度为偶数的点，等于它就被拿走了。

　　因此可以看成是对深度为奇数的点玩Nim游戏。

　　但是$b_{p} = 0$的点并不会对它的父节点产生影响，因此它变成一个子游戏。

　　最后判断一下每个子游戏深度为奇数的点的异或和是否为0就能判断胜负了。

Code

  1 #include <iostream>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <cstdio>
  5 using namespace std;
  6 typedef bool boolean;
  7 
  8 typedef class IO {
  9     protected:
 10         const static int Limit = 65536;
 11         FILE* file;
 12 
 13         int ss, st;
 14         char buf[Limit];
 15     public:
 16         IO():file(NULL)    {    };
 17         IO(FILE* file):file(file) {    }
 18 
 19         void open(FILE *file) {
 20             this->file = file;
 21         }
 22 
 23         char pick() {
 24             if (ss == st)
 25                 st = fread(buf, 1, Limit, file), ss = 0;//, cerr << "Str: " << buf << "ED " << st << endl;
 26             return buf[ss++];
 27         }
 28 }IO;
 29 
 30 #define digit(_x) ((_x) >= ‘0‘ && (_x) <= ‘9‘)
 31 
 32 IO& operator >> (IO& in, int& u) {
 33     char x;
 34     while (~(x = in.pick()) && !digit(x));
 35     for (u = x - ‘0‘; ~(x = in.pick()) && digit(x); u = u * 10 + x - ‘0‘);
 36     return in;
 37 }
 38 
 39 IO in (stdin);
 40 
 41 typedef class Edge {
 42     public:
 43         int ed, nx;
 44 
 45         Edge(int ed = 0, int nx = 0):ed(ed), nx(nx) {    }
 46 }Edge;
 47 
 48 const int N = 1e5 + 5;
 49 
 50 typedef class MapManager {
 51     public:
 52         int ce;
 53         int h[N];
 54         Edge es[N];
 55 
 56         void init(int n) {
 57             ce = -1;
 58             memset(h, -1, sizeof(int) * (n + 1));
 59         }
 60 
 61         void addEdge(int u, int v) {
 62             es[++ce] = Edge(v, h[u]);
 63             h[u] = ce;            
 64         }
 65 
 66         Edge& operator [] (int p) {
 67             return es[p];
 68         }
 69 }MapManager;
 70 
 71 int n;
 72 int ar[N], br[N];
 73 MapManager g;
 74 
 75 inline void init() {
 76     in >> n;
 77     g.init(n);
 78     for (int i = 1; i <= n; i++)
 79         in >> ar[i];    
 80     for (int i = 1; i <= n; i++)
 81         in >> br[i];
 82     for (int i = 1, u, v; i < n; i++) {
 83         in >> u >> v;
 84         g.addEdge(u, v);
 85         g.addEdge(v, u);
 86     }
 87 }
 88 
 89 int res;
 90 void dfs(int p, int fa, int dep) {
 91     int r = ar[p];
 92     for (int i = g.h[p]; ~i; i = g[i].nx) {
 93         int e = g[i].ed;
 94         if (e == fa)
 95             continue;
 96         dfs(e, p, (br[e]) ? (dep + 1) : (1));
 97         r -= ar[e] * br[e];
 98     }
 99     if (dep & 1)
100         res = res ^ r;
101 }
102 
103 inline void solve() {
104     res = 0;
105     dfs(1, 0, 1);
106     puts((res) ? ("YES") : ("NO"));
107 }
108 
109 int T;
110 int main() {
111     freopen("meal.in", "r", stdin);
112     freopen("meal.out", "w", stdout);
113     in >> T;
114     while (T--) {
115         init();
116         solve();
117     }
118     return 0;
119 }

Problem B

Problem C naive

技术分享图片

　　考虑一个跨过多个串的回文子串大概是长什么样的：

技术分享图片

　　首先可以枚举回文中心。然后不断向两边扩展，如果两边遇到边界，那么这是一个回文串，显然答案无穷大。

　　如果一端遇到边界，那么我们需要找另一个串在这里拼接，继续延伸。

　　对于一个还可以进行扩展的串一定存在左边或者右边存在一段连续的串不在当前的回文子串内，另一端恰好是回文子串的一个边界。而扩展的时候恰好与这一段串有关而与已经在回文子串中串无关。

技术分享图片

　　如果一个回文子串两边不能再扩展了（被其他字符封死了），那么就只能用它来更新答案了。

　　感觉这个转移很像一个图。

　　考虑把每个串的每个前缀未在回文子串中，以及后缀未在回文子串中看作一个点。

　　首先枚举回文中心，如果达到边界$S$就向对应的点连边。否则直接更新答案。

　　然后枚举任意一个前缀和后缀，枚举下一个拼接的串。如果没有被封死就连向另一个点，否则连向$T$。（感觉口胡不清楚，拼接方式见下图）

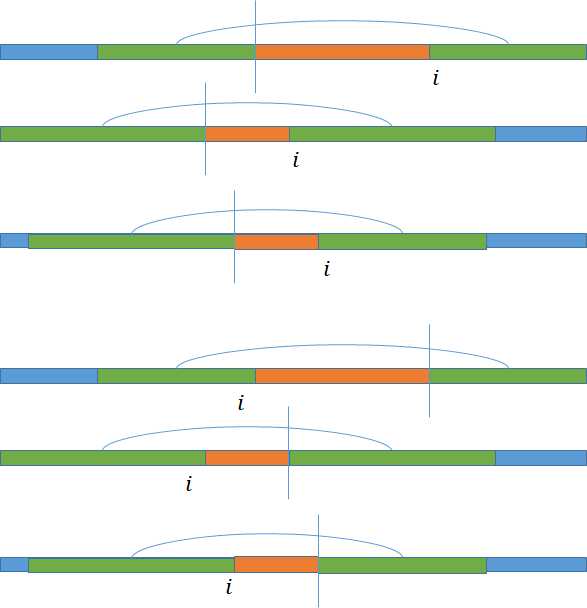
技术分享图片

　　（$i$是当前枚举的位置，橙色表示当前的回文子串，注意，它可能跨过了好几个串，蓝色表示还可以使用的部分，绿色是新增的部分，竖线与$i$异侧的一边是新拼接的串）

　　对于Infinity的情况相当于有环，且能从$S$出发到达。否则答案是最长路。这个可以用拓扑序求出。

　　计算下一个拼接串时能够增加当前回文子串的长度的多少需要求两个串的LCP之类的东西。

　　用后缀数组和st表可以做到$O(1)$查询。

Code

  1 #include <algorithm>
  2 #include <iostream>
  3 #include <cassert>
  4 #include <cstdlib>
  5 #include <cstring>
  6 #include <cstdio>
  7 #include <vector>
  8 #include <queue>
  9 using namespace std;
 10 typedef bool boolean;
 11 
 12 const int N = 105, L = 100005, sL = 1e5 + 5, sL2 = (sL + (L << 2)) << 1;
 13 const int bzmax = 20;
 14 
 15 int n;
 16 char strs[N][L], ss[sL2];
 17 int lenss = 0, res = 0;
 18 int pisa[N], rpisa[N], length[N];
 19 char mstr[L << 1];
 20 int palir[L << 1];
 21 
 22 inline void init() {
 23     scanf("%d", &n);
 24     for (int i = 1; i <= n; i++) {
 25         scanf("%s", strs[i] + 1);
 26         length[i] = strlen(strs[i] + 1);
 27     }
 28 }
 29 
 30 typedef class Pair3 {
 31     public:
 32         int x, y, id;
 33 
 34         Pair3(int x = 0, int y = 0, int id = 0):x(x), y(y), id(id) {    }
 35 
 36         boolean operator != (Pair3 b) {
 37             return x != b.x || y != b.y;
 38         }
 39 }Pair3;
 40 
 41 char mkspliter() {
 42 //    return rand() % 95 + 1;
 43     return ‘#‘;
 44 }
 45 
 46 int sa[sL2], rk[sL2];
 47 int cnt[sL2];
 48 Pair3 ps[sL2], tps[sL2];
 49 
 50 inline void radix_sort(Pair3 *ps, int n) {
 51     memset(cnt, 0, sizeof(int) * (n + 1));
 52     for (int i = 1; i <= n; i++)
 53         cnt[ps[i].y]++;
 54     for (int i = 1; i <= n; i++)
 55         cnt[i] += cnt[i - 1];
 56     for (int i = 1; i <= n; i++)
 57         tps[cnt[ps[i].y]--] = ps[i];
 58 
 59     memset(cnt, 0, sizeof(int) * (n + 1));
 60     for (int i = 1; i <= n; i++)
 61         cnt[tps[i].x]++;
 62     for (int i = 1; i <= n; i++)
 63         cnt[i] += cnt[i - 1];
 64     for (int i = n; i; i--)
 65         ps[cnt[tps[i].x]--] = tps[i];
 66 }
 67 
 68 inline void build_sa() {
 69     int cur = 0;
 70     for (int i = 1; i <= n; i++) {
 71         ss[++cur] = mkspliter();
 72         pisa[i] = cur + 1;
 73         for (int j = 1; j <= length[i]; j++)
 74             ss[++cur] = strs[i][j];
 75         ss[++cur] = mkspliter();
 76     }
 77     for (int i = n; i; i--) {
 78         ss[++cur] = mkspliter();
 79         rpisa[i] = cur + 1;
 80         for (int j = length[i]; j; j--)
 81             ss[++cur] = strs[i][j];
 82         ss[++cur] = mkspliter();
 83     }
 84     lenss = cur;
 85 
 86     int m = 256;
 87     memset(cnt, 0, sizeof(int) * (m + 1));
 88     for (int i = 1; i <= lenss; i++)
 89         cnt[ss[i]] = 1;
 90     for (int i = 1; i <= m; i++)
 91         cnt[i] += cnt[i - 1];
 92     for (int i = 1; i <= lenss; i++)
 93         rk[i] = cnt[ss[i]];
 94     
 95     for (int k = 0; k < bzmax; k++) {
 96         for (int i = 1, j = 1 + (1 << k); j <= lenss; i++, j++)
 97             ps[i] = Pair3(rk[i], rk[j], i);
 98         for (int i = lenss - (1 << k) + 1; i <= lenss; i++)
 99             ps[i] = Pair3(rk[i], 0, i);
100         radix_sort(ps, lenss);
101         m = 0;
102         for (int i = 1; i <= lenss; i++)
103             rk[ps[i].id] = ((i == 1 || ps[i] != ps[i - 1]) ? (++m) : (m));
104         if (m == lenss)
105             break;
106     }
107 
108     for (int i = 1; i <= lenss; i++)
109         sa[rk[i]] = i;
110 }
111 
112 int hei[sL2], log2[sL2];
113 int st[sL2][bzmax];
114 void get_height() {
115     for (int i = 1, j, k = 0; i <= lenss; i++) {
116         if (rk[i] > 1) {
117             for (j = sa[rk[i] - 1]; i + k <= lenss && j + k <= lenss && ss[i + k] == ss[j + k]; k++);
118             hei[rk[i]] = k;
119         }
120         if (k)
121             k--;
122     }
123 
124     log2[1] = 0;
125     for (int i = 2; i <= lenss; i++)
126         log2[i] = log2[i >> 1] + 1;
127     for (int i = 1; i <= lenss; i++)
128         st[i][0] = hei[i];
129     for (int j = 1; j < bzmax; j++)
130         for (int i = 1; (i + (1 << j)) - 1 <= lenss; i++)
131             st[i][j] = min(st[i][j - 1], st[(i + (1 << (j - 1)))][j - 1]);
132 }
133 
134 int query(int l, int r) {
135     int p = log2[(r - l + 1)];
136     return min(st[l][p], st[r - (1 << p) + 1][p]);
137 }
138 
139 int lcp(int a, int b) {
140     int l = rk[a], r = rk[b];
141     if (l > r)
142         swap(l, r);
143     int rt = query(l + 1, r);
144 //    cerr << a << " " << b << " " << rt << endl;
145     return rt;
146 }
147 
148 int prefix(int id, int p) {    return pisa[id] + p - 1;            }
149 int suffix(int id, int p) {    return rpisa[id] + length[id] - p;    }
150 
151 #define pii pair<int, int>
152 #define fi first
153 #define sc second
154 
155 int S = 0, T = sL2 - 1, All = sL2 - 2;
156 vector<pii> g[sL2];
157 
158 void addEdge(int u, int v, int w) {
159     g[u].push_back(pii(v, w));
160 //    if (u == 551 && v == prefix(6, 113))
161 //        cerr << u << "->" << v << " " << w << endl;
162 }
163 
164 void infinity() {
165     puts("Infinity");
166     exit(0);
167 }
168 
169 void manacher(int id, char* str, int n) {
170     mstr[0] = ‘-‘;
171     mstr[1] = ‘#‘;
172     int len = 1;
173     for (int i = 1; i <= n; i++) {
174         mstr[++len] = str[i];
175         mstr[++len] = ‘#‘;
176     }
177     mstr[++len] = ‘+‘;
178 
179     int pos = 0, R = 0;
180     for (int i = 1; i < len; i++) {
181         int r = 1;
182         if (i <= R)
183             r = min(palir[2 * pos - i] , R - i + 1);
184         while (mstr[i - r] == mstr[i + r])
185             r++;
186         if (i + r - 1 > R)
187             R = i + r - 1, pos = i;
188         palir[i] = r;
189         if (i - r == 0 && i + r == len)
190             infinity();
191         if (i - r == 0) {
192             int used, rp = i >> 1;
193             if (mstr[i] == ‘#‘)
194                 used = 2 * rp;
195             else
196                 used = 2 * rp - 1;
197             addEdge(S, suffix(id, used + 1), used);
198         } else if (i + r == len) {
199             int rp = i >> 1, li = length[id];
200             int used, rest;
201             if (mstr[i] == ‘#‘)
202                 used = (li - rp) << 1, rest = li - used;
203             else
204                 used = ((li - rp) << 1) + 1, rest = li - used;
205             addEdge(S, prefix(id, rest), used);
206         } else
207             res = max(res, r - 1);
208     }
209 
210 }
211 
212 void complete_graph() {
213     for (int i = 1; i <= n; i++) {
214         addEdge(All, prefix(i, length[i]), 0);
215         addEdge(All, suffix(i, 1), 0);
216     }
217     
218     for (int id = 1; id <= n; id++) {
219         // suffix is available
220         for (int i = 1, rest; i <= length[id]; i++) {
221             rest = length[id] - i + 1;
222             for (int j = 1, lj, w; j <= n; j++) {
223                 lj = length[j];
224                 w = lcp(prefix(id, i), suffix(j, lj));
225                 w = min(w, min(lj, rest));
226                 if (w == rest && w == lj) {
227                     addEdge(suffix(id, i), All, w << 1);
228                     continue;
229                 }
230                 if (w == rest)
231                     addEdge(suffix(id, i), prefix(j, lj - w), w << 1);
232                 else if (w == lj)
233                     addEdge(suffix(id, i), suffix(id, i + w), w << 1);
234                 else
235                     addEdge(suffix(id, i), T, w << 1);
236             }    
237         }
238         
239         // prefix
240         for (int i = 1; i <= length[id]; i++) {
241             for (int j = 1, lj, w; j <= n; j++) {
242                 lj = length[j];
243                 w = lcp(suffix(id, i), prefix(j, 1));
244                 w = min(w, min(i, lj));
245                 if (w == i && w == lj) {
246                     addEdge(prefix(id, i), All, w << 1);
247                     continue;
248                 }
249                 if (w == i)
250                     addEdge(prefix(id, i), suffix(j, w + 1), w << 1);
251                 else if (w == lj)
252                     addEdge(prefix(id, i), prefix(id, i - w), w << 1);
253                 else
254                     addEdge(prefix(id, i), T, w << 1);
255             } 
256         }
257     }
258 }
259 
260 int deg[sL2];
261 boolean vis[sL2];
262 void dfs(int p) {
263     vis[p] = true;
264     for (int i = 0; i < (signed) g[p].size(); i++) {
265         int e = g[p][i].fi;
266         deg[e]++;
267         if (!vis[e])
268             dfs(e);
269     }
270 }
271 
272 int f[sL2];
273 queue<int> que;
274 inline void topu() {
275     que.push(S);
276     while (!que.empty()) {
277         int e = que.front();
278         que.pop();
279         res = max(res, f[e]);
280         for (int i = 0; i < (signed) g[e].size(); i++) {
281             int eu = g[e][i].fi;    
282             f[eu] = max(f[eu], f[e] + g[e][i].sc);
283             res = max(res, f[eu]);
284             deg[eu]--;
285             if (!deg[eu])
286                 que.push(eu);
287         }
288     }
289 }
290 
291 inline void solve() {
292     build_sa();
293 //    cerr << ss + 1 << endl;
294     get_height();
295     for (int i = 1; i <= n; i++)
296         manacher(i, strs[i], length[i]);
297     complete_graph();
298     dfs(S);
299     topu();
300     for (int i = 1; i < sL; i++)
301         if (vis[i] && deg[i])
302             infinity();
303     printf("%d\n", res);
304 }
305 
306 int main() {
307     freopen("naive.in", "r", stdin);
308     freopen("naive.out", "w", stdout);
309     srand(233u);
310     init();
311     solve();
312     return 0;
313 }

Problem C

2018.2.23 省选模拟赛

标签：dep 负数奇数 line split 过多 tle span signed

原文地址：https://www.cnblogs.com/yyf0309/p/9534571.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行