标签:ext rem dhs lld apu ant obs using ppi
生活中我们总是少不了组合数问题
今天我就来讲一讲有关组合数的问题
我给你3个颜色不同的球,让你算出一共有多少种排列
我们画一下:
如图所示,答案一共6种
那么这个6又是怎么来的呢?
假设第一步我们选了红色
那么第二步,我们就只剩下蓝色和黄色可选。
第二步如果我选了蓝色,那么第三步我就只能选黄色。
反之,如果我选了黄色,第三步我就只能选蓝色(莫名像递归)
合起来,在第一次选红色的情况下,我们一共可以得到两个不同的排列
当然,第一次也可以选蓝色或者是黄色,所以答案有2+2+2=2*3=6种
如果有n种不同颜色的小球,那么
第一次选择有n种,第二次选择有n-1种......最后一次选择有1种可能。
所以一共有n*(n-1)*(n-2)*……*1种方案
用一棵树表示上面的栗子(n=3)就是这样:
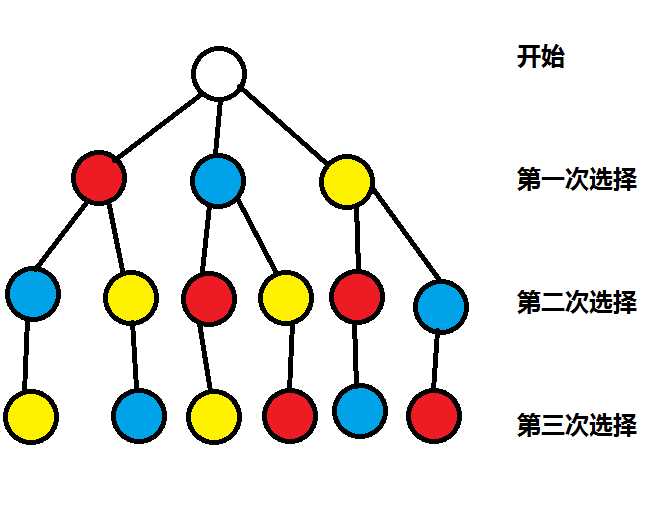
由此,我们可以得到全排列公式:
Pn(P表示全排列)=n*(n-1)*(n-2)*……*1=n!;
这不是太简单了???大佬们嘲笑本蒟蒻
好,那么我增加一下难度
这回我的球数变到4个
还是三种颜色,就是红球变成了两个
这回又是怎样呢?
我们画一下

(这里请将绿色看做第二个红色)
但是这两种其实是一个方案

所以,总方案数要除以2
那么如果有三个红球呢?
答案就是:所有球全排列数/红色球的全排列数
根据这个思想,当有多个颜色相同的球时,排列数=:
P(总球数)/(P(第1种颜色球的数量)*P(第2种颜色球的数量)*……*P(第n种颜色球的数量))
这就是组合去重
解决了全排列问题,我们看另一个经典问题:
一共有n个人,我们要从中选取m个人,求方案数
我们思路往往是这样的:
选第一个人有n种可能性,第二个人有(n-1)种可能性……
但显然不对,为什么呢?
我们还是列举一下(n=4,m=3,不同颜色代表一个人):

我们会发现,1,4,7,10,19,22号其实是一种方案
所以方案数实际上要除以6
。。。好吧,我来举个栗子
刚才是4个人(A,B,C,D),我们要选3个人
那么我们第一次有4种选择,第二次有3种选择,第三次有2种选择
乘起来是24
但不同于全排列的是,我第一个人选A与第二个人选A,第三个人选A并没有什么不同
也就是说,同样是(A,B,C)这种方案,我们选取时,会被选取6(m!)次
(A,B,C)(A,C,B)(B,A,C)(B,C,A)(C,A,B)(C,B,A)
所以我们要去重
所以Cnm=n*(n-1)*……(n-m+1)/Pm
看下面这个三角形:

你能发现什么呢?
大多数人都能发现,第n行第m个数=第n-1行第m-1个数+第n-1行第m个数(v[n][m]=v[n-1][m-1]+v[n-1][m])
下面我们把图改一下,标上编号:

我们会发现v[n][m]居然=Cnm!
我们来证明一下:

得证。(看不懂的请跳过,背公式就行)
那么这有用什么用呢?
想想看,如果你要求一个区间内的所有组合数,那么你按公式的话,每次要算m*2次
但如果你用递推组合数,算一次加法就好了
(如果n,m没有大到离谱,甚至可以省掉逆元)
快得很
想要例题出门左转组合数问题(noip2016Day2T1)
我这里就贴代码了:
#include<iostream> #include<cstdio> using namespace std; int x[2005][2005],a,b,c,n,m,t,k,ans[2005][2005]; int main() { scanf("%d%d",&t,&k); x[1][1]=1; for(a=0;a<=2000;a++) { x[a][0]=1; } for(a=2;a<=2000;a++) { for(b=1;b<=a;b++) { x[a][b]=x[a-1][b-1]+x[a-1][b]; x[a][b]%=k; } } for(a=2;a<=2000;a++) { for(b=1;b<=a;b++) { ans[a][b]=ans[a-1][b]+ans[a][b-1]-ans[a-1][b-1]; if(x[a][b]==0) { ans[a][b]++; } } ans[a][a+1]=ans[a][a]; } for(a=1;a<=t;a++) { scanf("%d%d",&n,&m); if(m>n) { m=n; } printf("%d\n",ans[n][m]); } }
不过刚才我说的有一个条件:n,m没有大到离谱
那要是大到离谱呢?(n=6653525,m=4784854,对P=19260817取模)
我们请出Lucas定理
当p=质数时
Cnm(modp)=C(n%p)(m%p)*C(n/p)(m/p)
(这里没有证明,因为我的证明基于费马小定理和二项式定理,而这些不在本篇的探讨范围)
这样,复杂度可以降到logpn,这样就可以过啦
不过,Lucas一般是要求逆元的
详见前面几期的Luogu日报(不过好像被和谐了)
可以看一下我的Lucas板子:
#include<iostream> #include<cstdio> using namespace std; long long n,m,p,t,ny[100005]; void qny()//求逆元 { ny[1]=1; for(register int a=2;a<=p-1;a++) { ny[a]=(p-(p/a))*ny[p%a]%p; } } int zhs(int q,int x)//求组合数 { if(q==0) { return 1; } long long ltt=1; for(register int a=1;a<=q;a++) { ltt*=ny[a]; ltt%=p; } for(register int a=1;a<=q;a++) { ltt*=(x-a+1); ltt%=p; } return ltt; } long long lucas(int s,int t)//主体部分 { if(t==0) { return 1; } else { return (lucas(s/p,t/p)*zhs(s%p,t%p))%p; } } int main() { scanf("%d",&t); p=19260817; qny(); for(int i=1;i<=t;i++) { scanf("%d%d",&n,&m); printf("%lld\n",lucas(m,n)); } }
当p!=质数时,也是有办法解的
那就是扩展Lucas
不过那是基于CRT(中国剩余定理)的
本人不做深入研究
有兴趣的大佬可自行百度
标签:ext rem dhs lld apu ant obs using ppi
原文地址:https://www.cnblogs.com/ztz11/p/9519167.html