标签:for style *** sequence info height 傅立叶变换 define 合并
1. 其实这个项目难点在于,能不能采集到高质量的钢琴音调。先看一下FFT相关程序。
FFT 并不是一种新的变换,它是离散傅立叶变换(DFT)的一种快速算法。由于我们在计算 DFT 时一次复数乘法需用四次实数乘法和二次实数加法;一次复数加法则需二次实数加法。每运算一个 X(k)需要 4N 次复数乘法及 2N+2(N-1)=2(2N-1)次实数加法。所以整个 DFT 运算总共需要 4N^2 次实数乘法和 N*2(2N-1)=2N(2N-1)次实数加法。如此一来,计算时乘法次数和加法次数都是和 N^2 成正比的,当 N 很大时,运算量是可观的,因而需要改进对 DFT 的算法减少运算速度。根据傅立叶变换的对称性和周期性,我们可以将 DFT 运算中有些项合并。我们先设序列长度为 N=2^L,L 为整数。将 N=2^L 的序列 x(n)(n=0,1,……,N-1),按 N 的奇偶分成两组,也就是说我们将一个 N 点的 DFT 分解成两个 N/2 点的 DFT,他们又重新组合成一个如下式所表达的 N 点 DFT:一般来说,输入被假定为连续的。当输入为纯粹的实数的时候,我们就可以利用左右对称的特性更好的计算 FFT。
2. 代码部分
#include "myapp.h"
#include "csedu.h"
#include "scancode.h"
#include <math.h>
#define PI 3.1415926
#define SAMPLENUMBER 128
void InitForFFT();
void MakeWave();
int INPUT[SAMPLENUMBER],DATA[SAMPLENUMBER];
float fWaveR[SAMPLENUMBER],fWaveI[SAMPLENUMBER],w[SAMPLENUMBER];
float sin_tab[SAMPLENUMBER],cos_tab[SAMPLENUMBER];
main()
{
int i;
InitForFFT();
MakeWave();
for ( i=0;i<SAMPLENUMBER;i++ )
{
fWaveR[i]=INPUT[i];
fWaveI[i]=0.0f;
w[i]=0.0f;
}
FFT(fWaveR,fWaveI);
for ( i=0;i<SAMPLENUMBER;i++ )
{
DATA[i]=w[i];
}
while ( 1 ); // break point
}
void FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLENUMBER])
{
int x0,x1,x2,x3,x4,x5,x6,xx;
int i,j,k,b,p,L;
float TR,TI,temp;
/********** following code invert sequence ************/
for ( i=0;i<SAMPLENUMBER;i++ )
{
x0=x1=x2=x3=x4=x5=x6=0;
x0=i&0x01; x1=(i/2)&0x01; x2=(i/4)&0x01; x3=(i/8)&0x01;x4=(i/16)&0x01; x5=(i/32)&0x01; x6=(i/64)&0x01;
xx=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;
dataI[xx]=dataR[i];
}
for ( i=0;i<SAMPLENUMBER;i++ )
{
dataR[i]=dataI[i]; dataI[i]=0;
}
/************** following code FFT *******************/
for ( L=1;L<=7;L++ )
{ /* for(1) */
b=1; i=L-1;
while ( i>0 )
{
b=b*2; i--;
} /* b= 2^(L-1) */
for ( j=0;j<=b-1;j++ ) /* for (2) */
{
p=1; i=7-L;
while ( i>0 ) /* p=pow(2,7-L)*j; */
{
p=p*2; i--;
}
p=p*j;
for ( k=j;k<128;k=k+2*b ) /* for (3) */
{
TR=dataR[k]; TI=dataI[k]; temp=dataR[k+b];
dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p];
dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p];
dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p];
dataI[k+b]=TI+temp*sin_tab[p]-dataI[k+b]*cos_tab[p];
} /* END for (3) */
} /* END for (2) */
} /* END for (1) */
for ( i=0;i<SAMPLENUMBER/2;i++ )
{
w[i]=sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);
}
} /* END FFT */
void InitForFFT()
{
int i;
for ( i=0;i<SAMPLENUMBER;i++ )
{
sin_tab[i]=sin(PI*2*i/SAMPLENUMBER);
cos_tab[i]=cos(PI*2*i/SAMPLENUMBER);
}
}
void MakeWave()
{
int i;
for ( i=0;i<SAMPLENUMBER;i++ )
{
INPUT[i]=sin(PI*2*i/SAMPLENUMBER*3)*1024;
}
}
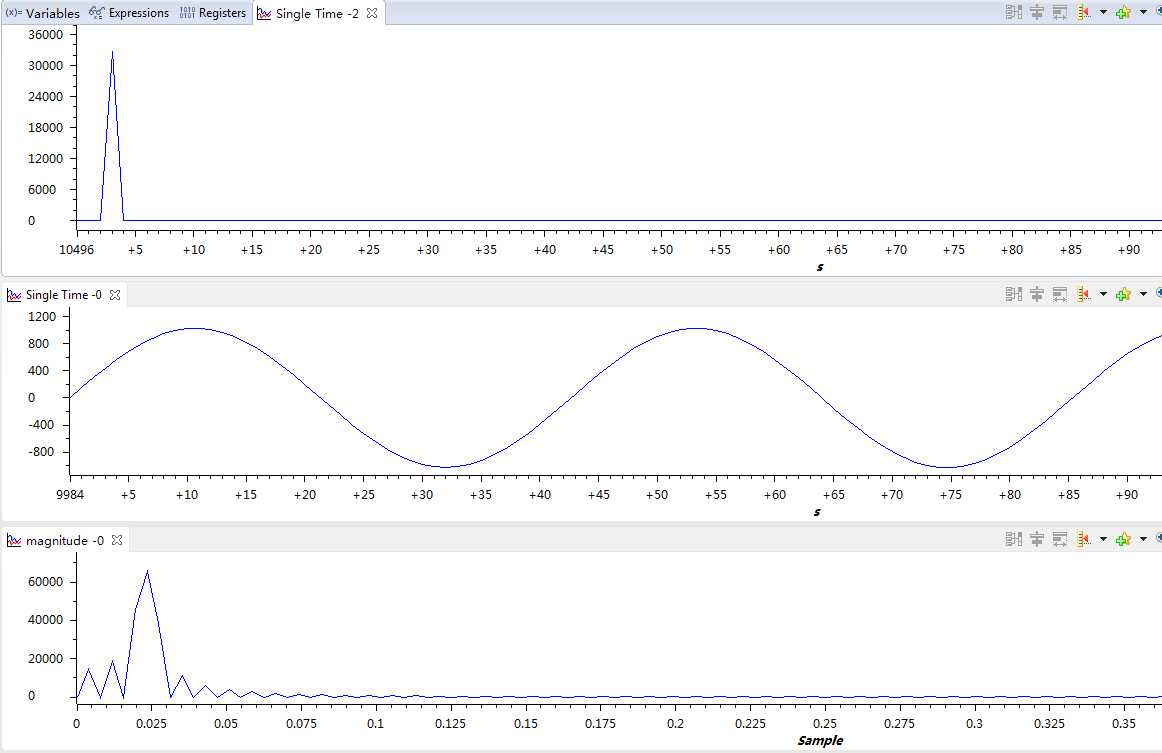
3. 启动调试,打开Tools->Graph,分别创建两个Singal Time(一个是原始的正选波形,一个是程序FFT得出的波形)和一个FFT Magnitude(CCS软件用FFT得出的波形),然后对比程序得出的和CCS帮得出的是否一致,就可以检查程序有没有问题。
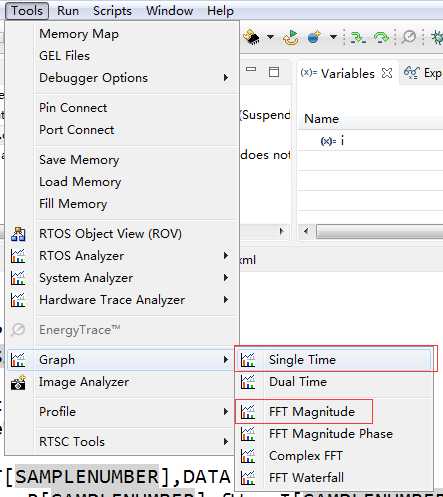
设置如下:
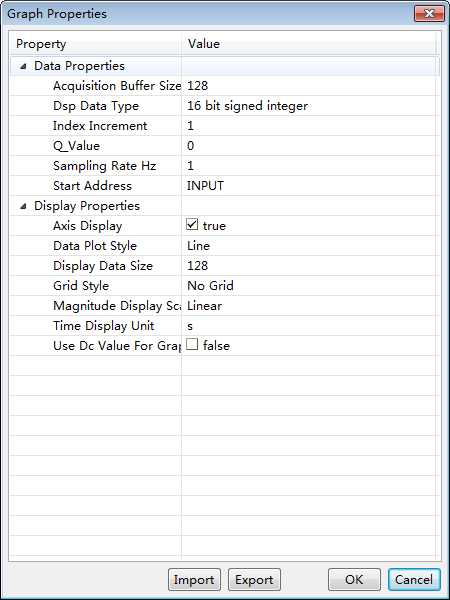
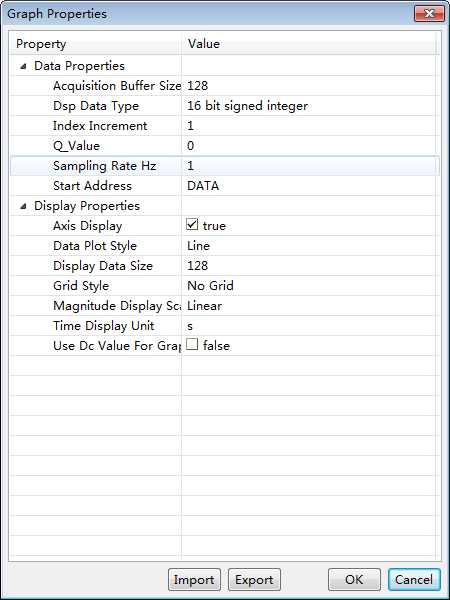
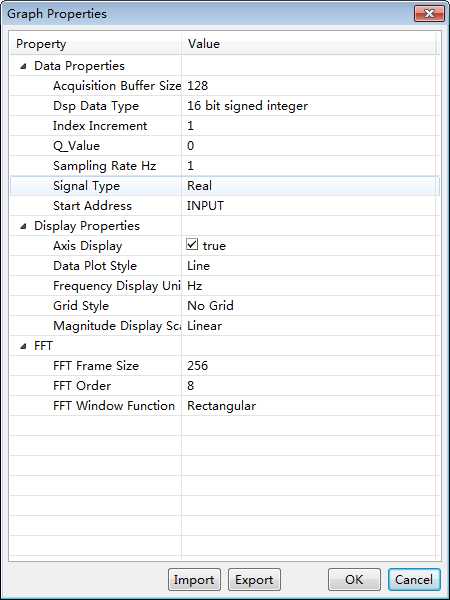
4. 最终得出的波形图,可以看出程序是正确的。
标签:for style *** sequence info height 傅立叶变换 define 合并
原文地址:https://www.cnblogs.com/429512065qhq/p/9534709.html