标签:substr rem 动态规划 bsp 技术 ++ 就是 ring ios
给定一个长度为N的数组,找出一个最长的单调自增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为6的数组A{5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4.
设长度为N的数组为{a0,a1, a2, ...an-1),则假定以aj结尾的数组序列的最长递增子序列长度为L(j),
则 L(j)={ max(L(i))+1, i<j且a[i]<a[j] }。
也就是说,我们需要遍历在j之前的所有位置i(从0到j-1),找出满足条件a[i]<a[j]的L(i),求出max(L(i))+1即为L(j)的值。最后,我们遍历所有的L(j)(从0到N-1),找出最大值即为最大递增子序列。时间复杂度为O(N^2)。
例如给定的数组为{5,6,7,1,2,8},则L(0)=1, L(1)=2, L(2)=3, L(3)=1, L(4)=2, L(5)=4。所以该数组最长递增子序列长度为4,序列为{5,6,7,8}。算法代码如下:
#include <iostream>
using namespace std;
#define len(a) (sizeof(a) / sizeof(a[0])) //数组长度
int lis(int arr[], int len)
{
int longest[len];
for (int i=0; i<len; i++)
longest[i] = 1;
for (int j=1; j<len; j++) {
for (int i=0; i<j; i++) {
if (arr[j]>arr[i] && longest[j]<longest[i]+1){ //注意longest[j]<longest[i]+1这个条件,不能省略。
longest[j] = longest[i] + 1; //计算以arr[j]结尾的序列的最长递增子序列长度
}
}
}
int max = 0;
for (int j=0; j<len; j++) {
cout << "longest[" << j << "]=" << longest[j] << endl;
if (longest[j] > max) max = longest[j]; //从longest[j]中找出最大值
}
return max;
}
int main()
{
int arr[] = {1, 4, 5, 6, 2, 3, 8}; //测试数组
int ret = lis(arr, len(arr));
cout << "max increment substring len=" << ret << endl;
return 0;
}
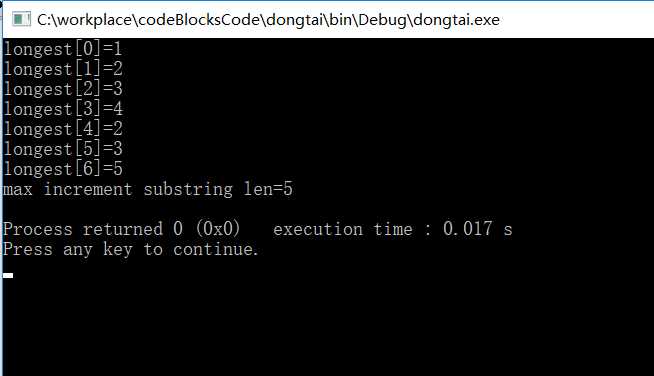
运行结果:
标签:substr rem 动态规划 bsp 技术 ++ 就是 ring ios
原文地址:https://www.cnblogs.com/cavinchen/p/9548088.html