标签:ptr 个数 解决方案 难点 释放空间 目的 lease i++ 方案
在特定领域内,某些变化虽然频繁,但可以抽象为某种规则。这时候,结合特定领域,将问题抽象为语法规则,从而给出该领域下的一般性解决方案。
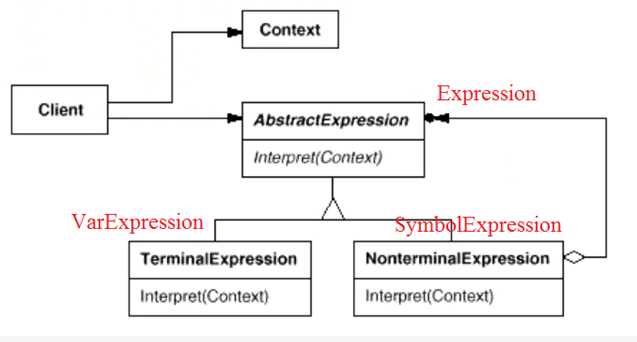
解析器模式:Interpreter
一些应用提供了内建(Build-In)的脚本或者宏语言来让用户定义他们能够在系统中进行的操作。
Interpreter模式的目的就是使用一个解释器为用户提供一个一门定义语言的语法表示的解释器,然后通过解释器来解释语言中的句子。
Interpreter模式提供了一个实现语法解释器的框架。
在软件构建过程中,如果某一特定领域的问题比较复杂,类似的结构不断的重复出现,如果使用普通的编程方式来实现将面临非常频繁的变化。
在这种情况下,将特定领域的问题表达为某种语法规则下的句子,然后构建一个解析器来解释这样的句子,从而达到解决问题的目的。
利用操作树来实现语法规则提取
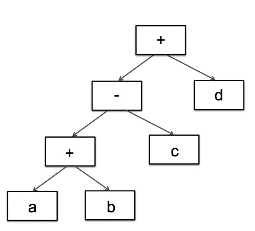
string expStr = "a+b-c+d"; //使用表达式树来表示规则
class Expression { public: virtual int interpreter(map<char, int> var)=0; //解析结果 virtual ~Expression(){} };
//变量表达式 class VarExpression: public Expression { char key; public: VarExpression(const char& key) { this->key = key; } int interpreter(map<char, int> var) override { return var[key]; } };
//符号表达式 class SymbolExpression : public Expression { // 运算符左右两个参数 protected: Expression* left; Expression* right; public: SymbolExpression( Expression* left, Expression* right): left(left),right(right){ } };
//加法运算 class AddExpression : public SymbolExpression { public: AddExpression(Expression* left, Expression* right): SymbolExpression(left,right){ } int interpreter(map<char, int> var) override { return left->interpreter(var) + right->interpreter(var); //执行操作 } }; //减法运算 class SubExpression : public SymbolExpression { public: SubExpression(Expression* left, Expression* right): SymbolExpression(left,right){ } int interpreter(map<char, int> var) override { return left->interpreter(var) - right->interpreter(var); } };
Expression* analyse(string expStr) { stack<Expression*> expStack; //使用栈来存储表达式 Expression* left = nullptr; Expression* right = nullptr; for(int i=0; i<expStr.size(); i++) { switch(expStr[i]) { case ‘+‘: // 加法运算 left = expStack.top(); //获取栈顶数据做左运算数 right = new VarExpression(expStr[++i]); //获取表达式下一个数做有运算数 expStack.push(new AddExpression(left, right)); //将运算结果入栈 break; case ‘-‘: // 减法运算 left = expStack.top(); right = new VarExpression(expStr[++i]); expStack.push(new SubExpression(left, right)); break; default: // 变量表达式 expStack.push(new VarExpression(expStr[i])); //不是符号,我们就进行入栈操作 } } Expression* expression = expStack.top(); //获取最后栈顶表达式返回出去就是结果 return expression; }
int main(int argc, const char * argv[]) { string expStr = "a+b-c+d-e"; //结构类似,容易抽象为语法规则,业务频繁变化 map<char, int> var; var.insert(make_pair(‘a‘,5)); var.insert(make_pair(‘b‘,2)); var.insert(make_pair(‘c‘,1)); var.insert(make_pair(‘d‘,6)); var.insert(make_pair(‘e‘,10)); Expression* expression= analyse(expStr); int result=expression->interpreter(var); //使用解析得到的表达式,可以获取结果返回 cout<<result<<endl; release(expression); return 0; }
void release(Expression* expression){ //释放表达式树的节点内存... }
给定一个语言,定义它的文法的一种表示,并定义一种解释器,这个解释器使用该表示来解释语言中的句子。
——《设计模式》GoF
设计模式---领域规则模式之解析器模式(Interpreter)
标签:ptr 个数 解决方案 难点 释放空间 目的 lease i++ 方案
原文地址:https://www.cnblogs.com/ssyfj/p/9550219.html