标签:amp 界面 规律 search sse const 时间 col 分享图片
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个77 行\times 5×5列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图66到图77 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
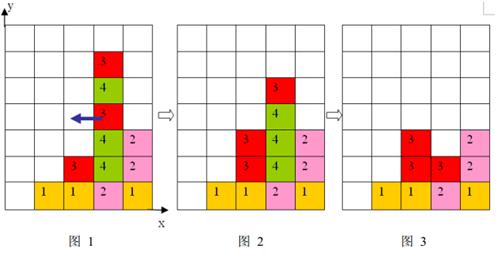
2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
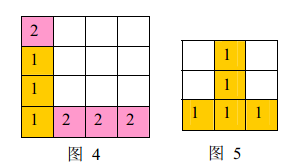
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图44 ,三个颜色为11 的方块和三个颜色为 22 的方块会同时被消除,最后剩下一个颜色为22的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
若有解,输出具体移动方案,否则输出-1.
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cassert>
using namespace std;
const int MAX_ROW = 10, MAX_COL = 10;
const int TotX = 5, TotY = 7;
int N;
struct Matrix
{
int A[MAX_ROW][MAX_COL];
private:
int GetHorSum(int x, int y)
{
int color = A[x][y];
int ans = 1;
for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
ans++;
for (int i = x + 1; i < TotX && A[i][y] == color; i++)
ans++;
return ans;
}
int GetVerSum(int x, int y)
{
int color = A[x][y];
int ans = 1;
for (int i = y + 1; i < TotY && A[x][i] == color; i++)
ans++;
for (int i = y - 1; i >= 0 && A[x][i] == color; i--)
ans++;
return ans;
}
void DropOne(int x, int y)
{
if (A[x][y])
for (int i = y - 1; i >= 0 && !A[x][i]; i--)
swap(A[x][i], A[x][i + 1]);
}
void DropAll()
{
for (int x = 0; x < TotX; x++)
for (int y = 0; y < TotY; y++)
DropOne(x, y);
}
void RemoveHor(int, int);
void RemoveVer(int, int);
bool Remove(int x, int y)
{
if (GetHorSum(x, y) >= 3)
{
RemoveHor(x, y);
DropAll();
return true;
}
if (GetVerSum(x, y) >= 3)
{
RemoveVer(x, y);
DropAll();
return true;
}
return false;
}
bool Search_Remove()
{
for (int x = 0; x < TotX; x++)
for (int y = 0; y < TotY && A[x][y]; y++)
if (Remove(x, y))
return true;
return false;
}
void RemoveAll()
{
while (Search_Remove());
}
public:
Matrix operator = (const Matrix& a)
{
memcpy(A, a.A, sizeof(a.A));
return *this;
}
bool operator == (const Matrix& a) const
{
return !memcmp(A, a.A, sizeof(A));
}
bool Empty()
{
for (int x = 0; x < TotX; x++)
if (A[x][0])
return false;
return true;
}
Matrix Move(int x, int y, int dir)
{
Matrix ans;
ans = *this;
assert(ans.A[x][y]);
assert(x + dir < TotX && x + dir >= 0);
if (ans.A[x + dir][y])
swap(ans.A[x][y], ans.A[x + dir][y]);
else
{
swap(ans.A[x][y], ans.A[x + dir][y]);
ans.DropAll();
}
ans.RemoveAll();
return ans;
}
};
void Matrix::RemoveHor(int x, int y)
{
int color = A[x][y];
A[x][y] = 0;
for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
{
if (GetVerSum(i, y) >= 3)
RemoveVer(i, y);
A[i][y] = 0;
}
for (int i = x + 1; i < TotX && A[i][y] == color; i++)
{
if (GetVerSum(i, y) >= 3)
RemoveVer(i, y);
A[i][y] = 0;
}
}
void Matrix::RemoveVer(int x, int y)
{
int color = A[x][y];
A[x][y] = 0;
for (int i = y - 1; y >= 0 && A[x][i] == color; i--)
{
if (GetHorSum(x, i) >= 3)
RemoveHor(x, i);
A[x][i] = 0;
}
for (int i = y + 1; y < TotY && A[x][i] == color; i++)
{
if (GetHorSum(x, i) >= 3)
RemoveHor(x, i);
A[x][i] = 0;
}
}
struct State
{
Matrix mat;
int X, Y, Dir;
}States[10];
bool Ok(int cnt)
{
for (int i = 0; i < cnt; i++)
if (States[i].mat == States[cnt].mat)
return false;
return true;
}
int Dfs(int cnt)
{
if (cnt > N)
return -1;
for (int x = 0; x < TotX; x++)
for (int y = 0; y < TotY && States[cnt - 1].mat.A[x][y]; y++)
{
States[cnt].X = x;
States[cnt].Y = y;
const Matrix& matFrom = States[cnt - 1].mat;
if (x <= TotX - 2 && matFrom.A[x + 1][y] != matFrom.A[x][y])
{
States[cnt].Dir = 1;
States[cnt].mat = States[cnt - 1].mat.Move(x, y, 1);
if (States[cnt].mat.Empty())
return cnt;
if (Ok(cnt))
{
int nextAns = Dfs(cnt + 1);
if (nextAns > -1)
return nextAns;
}
}
if (x >= 1 && !matFrom.A[x - 1][y])
{
States[cnt].Dir = -1;
States[cnt].mat = States[cnt - 1].mat.Move(x, y, -1);
if (States[cnt].mat.Empty())
return cnt;
if (Ok(cnt))
{
int nextAns = Dfs(cnt + 1);
if (nextAns > -1)
return nextAns;
}
}
}
return -1;
}
int main()
{
scanf("%d", &N);
for (int x = 0; x < TotX; x++)
for (int y = 0; scanf("%d", &States[0].mat.A[x][y]) && States[0].mat.A[x][y]; y++);
int cnt = Dfs(1);
if (cnt == -1)
printf("-1\n");
else
{
for (int i = 1; i <= cnt; i++)
printf("%d %d %d\n", States[i].X, States[i].Y, States[i].Dir);
}
return 0;
}
标签:amp 界面 规律 search sse const 时间 col 分享图片
原文地址:https://www.cnblogs.com/headboy2002/p/9557357.html