标签:基本 技巧 文献 tps 根据 线性 形式 今天 圆心
今天搬完了宿舍,发现去年复习复分析的时候整理了一下这一点,下面我将其$\TeX$化,原手写稿请见这里。
下面介绍一些复平面上的直观,因为我们解析几何通常以实数为基本,遇到复平面上的直线和圆时有时会很棘手,下面对此作一些整理。
注:之后$\overline{z}$均表示$z$的共轭。
首先是圆和直线的方程。
命题1. 复平面上直线与圆的方程共享同一种形式,他们是$$\alpha z\overline{z}+\beta z+\overline{\beta}\overline{z}+\gamma =0 \qquad \alpha,\gamma\in \mathbb{R}, \beta\in \mathbb{C}, \Delta=|\beta|^2-\alpha\gamma>0$$且圆心为$-\frac{\overline{\beta}}{\alpha}$, 半径为$\frac{\sqrt{\Delta}}{\alpha}$.
证明. 不难发现方程左边的虚部总为$0$, 故只有实部有效, 带入$z=x+yi$得到实部的方程是$$\alpha x^2+\alpha y^2+2 (\Re \beta) x - 2(\Im \beta) y + \gamma=\alpha\left[\left(x-\frac{\Re \beta}{\alpha}\right)^2+\left(y+\frac{\Im\beta}{\alpha}\right)^2\right]-\frac{(\Re \beta)^2+(\Im \beta)^2-\alpha\gamma}{\alpha}=0$$故原方程化为$$\left(x-\frac{\Re \beta}{\alpha}\right)^2+\left(y+\frac{\Im\beta}{\alpha}\right)^2=\frac{|\beta|^2-\alpha\gamma}{\alpha^2}=\frac{\Delta}{\alpha^2}$$从而圆心是$-\frac{\overline{\beta}}{\alpha}$, 半径为$\frac{\sqrt{\Delta}}{\alpha}$. 平凡的情况$\alpha=0$不难知道. $\square$
以下是一些注记。
注记. 以下是一些特殊情况.
- 当$\alpha=0$时, 原方程是一条直线, 方向为$i\overline{\beta}$(即$\beta$交换实部虚部)且实轴上经过$\frac{\gamma}{2\Re \beta}$虚轴上经过$i\frac{\gamma}{2\Im \beta}$两点, 进而经过$\frac{\gamma}{2\beta}$.
- 当$\beta=0$时, 原方程是一个圆心在原点的圆, 特别地, $z\overline{z}=1$就是单位圆周.
- 过原点角度为$\theta$的直线的方程是$\mathrm{e}^{-i\theta}z=\mathrm{e}^{i\theta }\overline{z}$.
然后是著名的M?bius变换。
定义(M?bius变换). 对于$A=\left(\begin{matrix} a& b\\ c& d\end{matrix}\right)\in \operatorname{GL}_2(\mathbb{C})$(即$ad-bc\neq 0$)定义扩充复平面到扩充复平面的映射$$\mu_{A}: z\longmapsto \frac{az+b}{cz+d}$$
例子. 有如下典型的M?bius变换,
- 平移. $z\mapsto z+b$.
- 旋转. $z\mapsto az$, $|a|=1$.
- 位似. $z\mapsto rz$, $r>0$.
- 标准反演. $z\mapsto 1/z$. 用极坐标写就是$r\mathrm{e}^{i\theta}\mapsto \frac{1}{r} \mathrm{e}^{-i\theta}$. 此时将方程$\alpha z\overline{z}+\beta z+\overline{b}\overline{z}+\gamma =0$变为$\gamma z\overline{z}+\overline{\beta} z+b\overline{z}+\alpha=0$, 圆心由$-\frac{\overline{\beta}}{\alpha}$变为$-\frac{\beta}{\gamma}$, 半径由$\frac{\sqrt{\Delta}}{\alpha}$变为$\frac{\sqrt{\Delta}}{\gamma}$. 如下图
实际上, 所有M?bius变换都可以由上述映射复合而来, 这本质上都是中学数学的技巧. 实际上, 用线性代数的话说, 他们分别对应着一些初等矩阵.
对于平移旋转和位似我们已经有直观,所以为了感受到M?bius变换,要直观感受反演显得关键。
命题(反演). 关于标准反演有如下直观
- 将圆心在$0$半径为$r$的圆映射为圆心在$0$半径为$1/r$的圆. 特别地, 保持单位圆周不动.
- 将过$0$以角度$\theta$的直线映为过$0$角度为$-\theta$的直线.
- 将过$0$的圆映射为直线. 特别地, 如果这个圆与单位圆相切, 这对应的直线与圆相切.
- 将与单位圆周正交的圆映为关于实轴的镜像.
证明. 前两者不难根据刻画或者方程得到. 后两者可以用初等几何论证, 第一个证明是利用了相似的原理, 第二个证明则是圆幂定理. $\square$
除了M?bius变换,还有著名的单位圆周内部的Blaschke变换
定义(Blaschke变换). 令$D$是闭单位圆盘, 对于$|\alpha|<1$, 定义Blaschke变换$$\varphi_{\alpha}: D\longrightarrow D\qquad z\longmapsto \frac{z-\alpha}{\overline{\alpha}z-1}$$
评注. 对于其映射定义良好(即像落在$D$中)可以初等验证, 也可以利用最大模原理证明边界上的像在单位圆周上即可.
命题. 关于Blaschke变换$\varphi_{\alpha}$有如下直观
- $\alpha\mapsto 0, 0\mapsto \alpha$.
- $\varphi_{\alpha}\circ \varphi_{\alpha}=\operatorname{id}_U$.
- 将圆周上的点$z$映射为$z$与$\alpha$连线与圆周相交的另一点.
- 用$\tau_{\theta}$表示绕着原点旋转$\theta$的变换, 则$\tau_{\theta}\circ \varphi_{\alpha}=\varphi_{\tau_{\theta}(\alpha)}\circ \tau_{\theta}$.
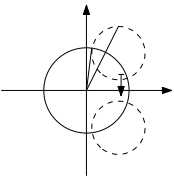
证明.第二点是因为因为$$z\mapsto w\iff \overline{\alpha}zw+\alpha=z+w$$对于第三点, 可以这样论证, 先不妨假定$\alpha$为实数, 如下图
中间左边的向量即为$\alpha$, 两边的角度分别是$\theta_1,\theta_2$(带方向, 图中一正一负), 外侧两腰长度为$1$. 则从左向右对应的复数分别为$$\mathrm{e}^{i\theta_1}, \alpha, \alpha\mathrm{e}^{i(\theta_1+\theta_2)},\mathrm{e}^{i\theta_2}$$两边之和等于中间之和即$$\mathrm{e}^{i\theta_1}+\mathrm{e}^{i\theta_2}=\alpha(\mathrm{e}^{i(\theta_1+\theta_2)}+1)$$这就说明$$\mathrm{e}^{i\theta_2}=\frac{\mathrm{e}^{i\theta_1}-\alpha}{\alpha\mathrm{e}^{i\theta_1}-1}$$这就证明了结论. $\square$
主要的参考文献是Rudin的《实分析与复分析》和著名的《复分析可视化原理》。
标签:基本 技巧 文献 tps 根据 线性 形式 今天 圆心
原文地址:https://www.cnblogs.com/XiongRuiMath/p/9557230.html