标签:col 也有 bsp bubuko 输出 一个 简单 blur 可靠性
1、关于平滑处理
“平滑处理“(smoothing)也称“模糊处理”(bluring),是一项简单且使用频率很高的图像处理方法。平滑处理的用途有很多,最常见的是用来减少图像上的噪点或者失真。在涉及到降低图像分辨率时,平滑处理是非常好用的方法。
2、图像滤波与滤波器
图像滤波,即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,是图像预处理中不可缺少的操作,其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。
消除图像中的噪声成分叫作图像的平滑化或滤波操作。信号或图像的能量大部分集中在幅度谱的低频和中频段是很常见的,而在较高频段,感兴趣的信息经常被噪声淹没。因此一个能降低高频成分幅度的滤波器就能够减弱噪声的影响。
图像滤波的目的有两个:一是抽出对象的特征作为图像识别的特征模式;另一个是为适应图像处理的要求,消除图像数字化时所混入的噪声。
而对滤波处理的要求也有两条:一是不能损坏图像的轮廓及边缘等重要信息;二是使图像清晰视觉效果好。
平滑滤波是低频增强的空间域滤波技术。它的目的有两类:一类是模糊;另一类是消除噪音。(各种“两",:))
空间域的平滑滤波一般采用简单平均法进行,就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关,邻域越大平滑的效果越好,但邻域过大,平滑会使边缘信息损失的越大,从而使输出的图像变得模糊,因此需合理选择邻域的大小。
关于滤波器,一种形象的比喻法是:我们可以把滤波器想象成一个包含加权系数的窗口,当使用这个滤波器平滑处理图像时,就把这个窗口放到图像之上,透过这个窗口来看我们得到的图像。
3、对线性滤波器的简介
线性滤波器:线性滤波器经常用于剔除输入信号中不想要的频率或者从许多频率中选择一个想要的频率。
几种常见的线性滤波器:
●允许低频率通过的低通滤波器。
●允许高频率通过的高通滤波器。
●允许一定范围频率通过的带通滤波器。
●阻止一定范围频率通过并且允许其它频率通过的带阻滤波器。
●允许所有频率通过、仅仅改变相位关系的全通滤波器。
●阻止一个狭窄频率范围通过的特殊带阻滤波器,陷波滤波器(Band-stop filter)。
4、关于滤波和模糊
关于滤波和模糊,大家往往在初次接触的时候会弄混淆,“一会儿说滤波,一会儿又说模糊,什么玩意儿啊”。
没关系,在这里,我们就来辨别一下,为大家扫清障碍。
我们上文已经提到过,滤波是将信号中特定波段频率滤除的操作,是抑制和防止干扰的一项重要措施。
为了方便说明,就拿我们经常用的高斯滤波来作例子吧。我们知道,滤波可分低通滤波和高通滤波两种。而高斯滤波是指用高斯函数作为滤波函数的滤波操作,至于是不是模糊,要看是高斯低通还是高斯高通,低通就是模糊,高通就是锐化。
其实说白了是很简单的,对吧:
高斯滤波是指用高斯函数作为滤波函数的滤波操作。
高斯模糊就是高斯低通滤波。
5、邻域算子与线性邻域滤波
邻域算子(局部算子)是利用给定像素周围的像素值的决定此像素的最终输出值的一种算子。而线性邻域滤波是一种常用的邻域算子,像素的输出值取决于输入像素的加权和,具体过程如下图。
邻域算子除了用于局部色调调整以外,还可以用于图像滤波,实现图像的平滑和锐化,图像边缘增强或者图像噪声的去除。本篇文章,我们介绍的主角是线性邻域滤波算子,即用不同的权重去结合一个小邻域内的像素,来得到应有的处理效果。
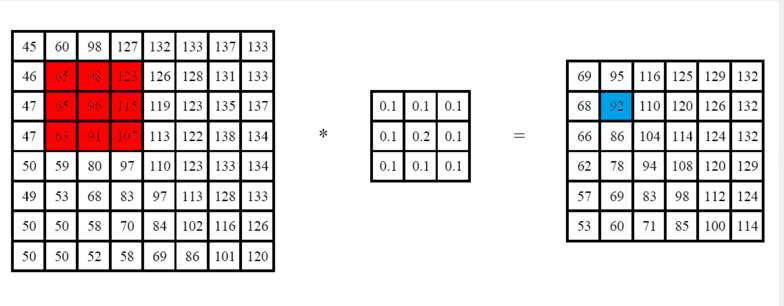
图注:邻域滤波(卷积):左边图像与中间图像的卷积产生右边图像。目标图像中蓝色标记的像素是利用原图像中红色标记的像素计算得到的。
线性滤波处理的输出像素值 是输入像素值
是输入像素值 的加权和 :
的加权和 :

其中的加权和为 ,我们称其为“核”,滤波器的加权系数,即滤波器的“滤波系数”。
上面的式子可以简单写作:

其中的加权和为 ,我们称其为“核”,滤波器的加权系数,即滤波器的“滤波系数”。
上面的式子可以简单写作:

其中f表示输入像素值,h表示加权系数“核“,g表示输出像素值
标签:col 也有 bsp bubuko 输出 一个 简单 blur 可靠性
原文地址:https://www.cnblogs.com/zhuifeng-mayi/p/9558052.html