标签:分层 出栈 分享图片 搜索 http 序列 遍历二叉树 i++ font
一、建立一个如下图所示的二叉树并打印出来。
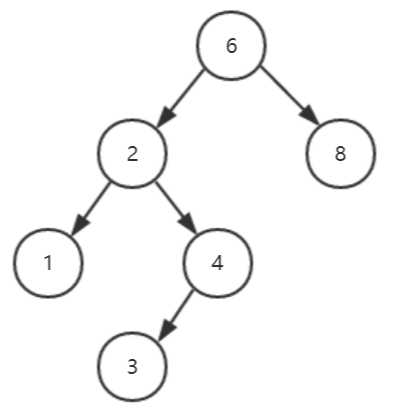
图 1
二、二叉树的建立
由于二叉树的定义是递归的,所以用递归的思想建立二叉树是很自然的想法。
1. 以前序遍历的方式
/* 以前序遍历的方式建立 */
BinaryTreeNode* create()
{
BinaryTreeNode *pRoot = nullptr;
char c;
cin >> c;
if(c == ‘#‘) {
return nullptr;
}
else {
pRoot = new BinaryTreeNode;
pRoot->value = c;
pRoot->lChild = create();
pRoot->rChild = create();
}
return pRoot;
}
补:只要输入序列621##43###8##,就会建立一个如图1所示的二叉树。序列中的‘#‘表示空结点,可用其作为递归终止的条件。
2. 根据中序序列和后序序列建立二叉树
如果只给出前序序列、中序序列或后序序列中的一种,则不能唯一确定一棵二叉树。但是如果给出中序序列和后序序列或者前序序列和中序序列就可以唯一确定一棵二叉树。
图1所示的二叉树的中序遍历序列是123468,后序遍历序列是134286,我们可通过输入这两个序列来建立一个如图1所示的二叉树。
/* 根据中序序列和后序序列来创建二叉树 */
BinaryTreeNode* create(int InOrd[], int PostOrd[], int n)
{
if(n == 0){ // 递归终止条件
return nullptr; // 此处应是一个空结点
}
BinaryTreeNode *pRoot = new BinaryTreeNode;
pRoot->value = PostOrd[n-1]; // 根结点的值
int lChildNum = 0; // 左子树的结点数
int rChildNum = 0; // 右子树的结点数
for(; lChildNum < n; ++lChildNum) {
if(InOrd[lChildNum] == pRoot->value)
break;
}
rChildNum = n - lChildNum - 1;
// 递归创建左右子树
pRoot->lChild = create(InOrd, PostOrd, lChildNum);
pRoot->rChild = create(InOrd + lChildNum + 1, PostOrd + lChildNum, rChildNum);
return pRoot;
}
分析:后序序列的最后一个元素一定是这棵树的根结点,由此结点的值去遍历中序序列,可得到左子树和右子树的结点个数,据此,再分别传入左子树和右子树的中序序列和后序序列来创建当前根结点的左孩子结点和右孩子结点。如此递归,便可建立一棵如图1所示的二叉树。
三、用递归的方式实现二叉树的前/中/后序遍历
/* 前序遍历 */
void PreOrderTraverse(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return;
cout << pRoot->value;
PreOrderTraverse(pRoot->lChild);
PreOrderTraverse(pRoot->rChild);
}
/* 中序遍历 */
void InOrderTraverse(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return;
InOrderTraverse(pRoot->lChild);
cout << pRoot->value;
InOrderTraverse(pRoot->rChild);
}
/* 后序遍历 */
void PostOrderTraverse(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return;
PostOrderTraverse(pRoot->lChild);
PostOrderTraverse(pRoot->rChild);
cout << pRoot->value;
}
四、用非递归的方式实现二叉树的前/中/后序遍历
1. 前序遍历
先从栈顶取出结点,如果该结点不为空,则访问该结点,同时把该结点的右子树和左子树依次入栈。
void PreOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BinaryTreeNode*> sck;
sck.push(pRoot);
BinaryTreeNode *pNode = nullptr;
while(!sck.empty()) {
pNode = sck.top();
sck.pop();
if(pNode != nullptr) {
cout << pNode->value;
sck.push(pNode->rChild);
sck.push(pNode->lChild);
}
}
}
2. 中序遍历
先把根结点入栈,然后再一直把左子树入栈,直到左子树为空,此时停止入栈。栈顶结点就是我们需要访问的结点,取栈顶结点p并访问。然后该结点可能有右子树,所以访问完结点p后还要判断p的右子树是否为空,如果为空则接下来要访问的结点在栈顶,所以将p赋值为null。如果不为空则将p赋值为其右子树的值。
/* 中序遍历 */
void InOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BinaryTreeNode*> sck;
BinaryTreeNode *pCur = pRoot;
while(!sck.empty() || pCur != nullptr) {
while(pCur != nullptr) {
sck.push(pCur);
pCur = pCur->lChild;
}
pCur = sck.top();
sck.pop();
cout << pCur->value;
if(pCur->rChild != nullptr)
pCur = pCur->rChild;
else
pCur = nullptr;
}
}
3. 后序遍历
对于任一结点P,将其入栈,然后沿其左子树一直往下搜索,直到搜索到没有左孩子的结点,此时该结点出现在栈顶,但是此时不能将其出栈并访问, 因此其右孩子还未被访问。所以接下来按照相同的规则对其右子树进行相同的处理。当访问完其右孩子时,该结点又出现在栈顶,此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出,在这个过程中,每个第一次不能出栈的结点都将两次出现在栈顶,并且只有在第二次出现在栈顶时,才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。
/* 后序遍历 */
struct BTNode {
BinaryTreeNode *pNode;
bool isFirst;
};
void PostOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BTNode*> sck;
BTNode *temp = nullptr;
BinaryTreeNode *pCur = pRoot;
while(pCur != nullptr || !sck.empty()) {
while(pCur != nullptr) {
BTNode *pBtn = new BTNode;
pBtn->pNode = pCur;
pBtn->isFirst = true;
sck.push(pBtn);
pCur = pCur->lChild;
}
temp = sck.top();
sck.pop();
if(temp->isFirst == true) {
sck.push(temp);
temp->isFirst = false;
pCur = temp->pNode->rChild;
}
else {
cout << temp->pNode->value;
pCur = nullptr;
}
}
}
分析,以图1所示的二叉树为例,如果不加入辅助变量来判断结点是否第一次出现在栈顶,那么将输出1348,其中有右子树的结点都将因第一次出现在栈顶而被弹出栈,然而第一次出现时并不会输出,所以结果输出将没有它们。
五、层次遍历
1. 使用队列的循环实现
/* 层次遍历 */
void LevelTraverse(BinaryTreeNode *pRoot)
{
queue<BinaryTreeNode*> que;
que.push(pRoot);
BinaryTreeNode *pNode = nullptr;
while(!que.empty()) {
pNode = que.front();
que.pop();
cout << pNode->value;
if(pNode->lChild != nullptr)
que.push(pNode->lChild);
if(pNode->rChild != nullptr)
que.push(pNode->rChild);
}
}
2. 使用递归实现
/* 层次遍历 */
void PrintNodeAtLevel(BinaryTreeNode *pRoot, int level)
{
if(pRoot == nullptr || level < 1) // 空树或层级不合理
return;
if(level == 1) {
cout << pRoot->value;
return;
}
// 左子树的 level - 1 级
PrintNodeAtLevel(pRoot->lChild, level - 1);
// 右子树的 level - 1 级
PrintNodeAtLevel(pRoot->rChild, level - 1);
}
void LevelTraverse(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return;
int height = GetHeight(pRoot); // 二叉树的高度
// 逐层打印
for(int i = 1; i <= height; i++) {
PrintNodeAtLevel(pRoot, i);
cout << endl;
}
}
分析:该解法得到的既是层次遍历的结果,又是二叉树分层输出的结果。
六、求树的高度
1. 使用递归实现
/* 求树的高度 */
int GetHeight(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr) return 0;
int leftHeight = GetHeight(pRoot->lChild);
int rightHeight = GetHeight(pRoot->rChild);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
2. 使用循环实现
利用循环求二叉树高度的思想是:一层一层地出队列。在我们每次访问完毕一层时,这时队列中存储的刚好是下一层的所有元素。所以在下一次循环开始时,首先记录该层的元素个数,一次性访问完这一层的所有元素。
/* 求树的高度 */
int GetHeight(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr) return 0;
int height = 0; // 树的高度
queue<BinaryTreeNode*> que;
que.push(pRoot);
BinaryTreeNode *pCur = nullptr;
// 实际上当每次循环开始时,队列中存储的刚好是将要访问的那一层的所有元素
while(!que.empty()) {
height++;
int curLevelNum = que.size(); // 当前层的结点数
// 弹出当前层所有元素
while(curLevelNum-- > 0) {
pCur = que.front();
que.pop();
// 将下一层的元素压入队列
if(pCur->lChild != nullptr)
que.push(pCur->lChild);
if(pCur->rChild != nullptr)
que.push(pCur->rChild);
}
}
return height;
}
七、总代码
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
struct BinaryTreeNode {
int value;
BinaryTreeNode *lChild;
BinaryTreeNode *rChild;
};
struct BTNode {
BinaryTreeNode *pNode;
bool isFirst;
};
int GetHeight(BinaryTreeNode *pRoot);
/* 根据中序序列和后序序列来创建二叉树 */
BinaryTreeNode* create(int InOrd[], int PostOrd[], int n)
{
if(n == 0){ // 递归终止条件
return nullptr; // 此处应是一个空结点
}
BinaryTreeNode *pRoot = new BinaryTreeNode;
pRoot->value = PostOrd[n-1]; // 根结点的值
int lChildNum = 0; // 左子树的结点数
int rChildNum = 0; // 右子树的结点数
for(; lChildNum < n; ++lChildNum) {
if(InOrd[lChildNum] == pRoot->value)
break;
}
rChildNum = n - lChildNum - 1;
// 递归创建左右子树
pRoot->lChild = create(InOrd, PostOrd, lChildNum);
pRoot->rChild = create(InOrd + lChildNum + 1, PostOrd + lChildNum, rChildNum);
return pRoot;
}
/* 非递归先序遍历 */
void PreOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BinaryTreeNode*> sck;
sck.push(pRoot);
BinaryTreeNode *pNode = nullptr;
while(!sck.empty()) {
pNode = sck.top();
sck.pop();
if(pNode != nullptr) {
cout << pNode->value;
sck.push(pNode->rChild);
sck.push(pNode->lChild);
}
}
}
/* 非递归中序遍历 */
void InOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BinaryTreeNode*> sck;
BinaryTreeNode *pCur = pRoot;
while(!sck.empty() || pCur != nullptr) {
while(pCur != nullptr) {
sck.push(pCur);
pCur = pCur->lChild;
}
pCur = sck.top();
sck.pop();
cout << pCur->value;
if(pCur->rChild != nullptr)
pCur = pCur->rChild;
else
pCur = nullptr;
}
}
/* 非递归后序遍历 */
void PostOrderTraverse(BinaryTreeNode *pRoot)
{
stack<BTNode*> sck;
BTNode *temp = nullptr;
BinaryTreeNode *pCur = pRoot;
while(pCur != nullptr || !sck.empty()) {
while(pCur != nullptr) {
BTNode *pBtn = new BTNode;
pBtn->pNode = pCur;
pBtn->isFirst = true;
sck.push(pBtn);
pCur = pCur->lChild;
}
temp = sck.top();
sck.pop();
if(temp->isFirst == true) {
sck.push(temp);
temp->isFirst = false;
pCur = temp->pNode->rChild;
}
else {
cout << temp->pNode->value;
pCur = nullptr;
}
}
}
/* 递归层次遍历 */
void PrintNodeAtLevel(BinaryTreeNode *pRoot, int level)
{
if(pRoot == nullptr || level < 1) // 空树或层级不合理
return;
if(level == 1) {
cout << pRoot->value;
return;
}
// 左子树的 level - 1 级
PrintNodeAtLevel(pRoot->lChild, level - 1);
// 右子树的 level - 1 级
PrintNodeAtLevel(pRoot->rChild, level - 1);
}
void LevelTraverse(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return;
int height = GetHeight(pRoot); // 二叉树的高度
// 逐层打印
for(int i = 1; i <= height; i++)
PrintNodeAtLevel(pRoot, i);
}
/* 循环求树的高度 */
int GetHeight(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr) return 0;
int height = 0; // 树的高度
queue<BinaryTreeNode*> que;
que.push(pRoot);
BinaryTreeNode *pCur = nullptr;
// 实际上当每次循环开始时,队列中存储的刚好是将要访问的那一层的所有元素
while(!que.empty()) {
height++;
int curLevelNum = que.size(); // 当前层的结点数
// 弹出当前层所有元素
while(curLevelNum-- > 0) {
pCur = que.front();
que.pop();
// 将下一层的元素压入队列
if(pCur->lChild != nullptr)
que.push(pCur->lChild);
if(pCur->rChild != nullptr)
que.push(pCur->rChild);
}
}
return height;
}
int main()
{
int InOrd[6] = {1, 2, 3, 4, 6, 8};
int PostOrd[6] = {1, 3, 4, 2, 8, 6};
BinaryTreeNode *pTree = create(InOrd, PostOrd, 6);
cout << "提示:二叉树创建完毕!" << endl;
cout << "提示:先序遍历二叉树..." << endl;
PreOrderTraverse(pTree);
cout << endl;
cout << "提示:中序遍历二叉树..." << endl;
InOrderTraverse(pTree);
cout << endl;
cout << "提示:后序遍历二叉树..." << endl;
PostOrderTraverse(pTree);
cout << endl;
cout << "提示:层次遍历二叉树..." << endl;
LevelTraverse(pTree);
cout << endl;
cout << "提示:树的高度为" << GetHeight(pTree) << endl;
return 0;
}
标签:分层 出栈 分享图片 搜索 http 序列 遍历二叉树 i++ font
原文地址:https://www.cnblogs.com/xzxl/p/9568838.html