时空限制4000ms / 128MB
题目描述
一个餐厅在相继的 N 天里,每天需用的餐巾数不尽相同。假设第 i 天需要 ri?块餐巾( i=1,2,...,N)。餐厅可以购买新的餐巾,每块餐巾的费用为 p 分;或者把旧餐巾送到快洗部,洗一块需 m 天,其费用为 f 分;或者送到慢洗部,洗一块需 n 天(n>m),其费用为 s 分(s<f)。
每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。
试设计一个算法为餐厅合理地安排好 N 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。
输入输出格式
输入格式:由标准输入提供输入数据。文件第 1 行有 1 个正整数 N,代表要安排餐巾使用计划的天数。
接下来的 N 行是餐厅在相继的 N 天里,每天需用的餐巾数。
最后一行包含5个正整数p,m,f,n,s。p 是每块新餐巾的费用; m 是快洗部洗一块餐巾需用天数; f 是快洗部洗一块餐巾需要的费用; n 是慢洗部洗一块餐巾需用天数; s 是慢洗部洗一块餐巾需要的费用。
输出格式:将餐厅在相继的 N 天里使用餐巾的最小总花费输出
输入输出样例
说明
N<=2000
ri<=10000000
p,f,s<=10000
时限4s
费用流建图好题。这题的建图很不一样,主要是难在怎么让程序跑满最大流。
具体建图参考图片:
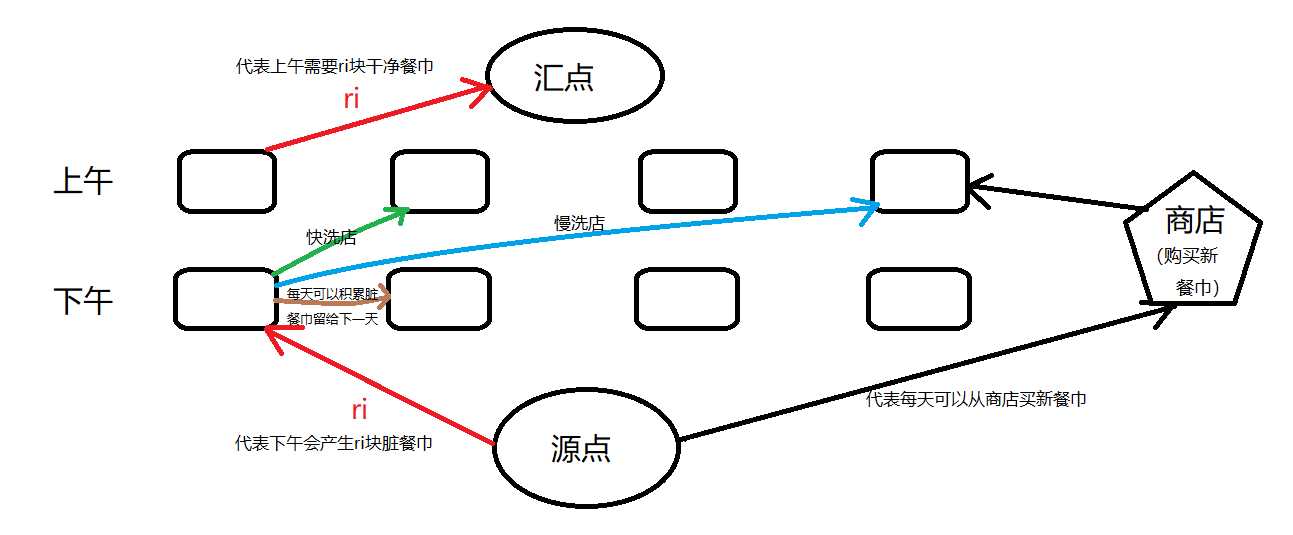

#include<bits/stdc++.h> #define INF INT_MAX/2 #define N 4200 using namespace std; struct ss { int u,v,flow,cost; }; vector<ss>edg; vector<int>edges[N]; int now_edges=0; void addedge(int u,int v,int flow,int cost) { edges[u].push_back(now_edges++); edg.push_back((ss){u,v,flow,cost}); edges[v].push_back(now_edges++); edg.push_back((ss){v,u,0,-cost}); } bool spfa(int s,int t,long long &flow,long long &cost) { int dis[N]; for(int i=0;i<N;i++)dis[i]=INF; dis[s]=0; int vis[N]={0}; vis[s]=1; queue<int>q; q.push(s); int pre[N]={0}; int addflow[N]; addflow[s]=INF; while(!q.empty()) { int now=q.front(); q.pop(); vis[now]=0; int Size=edges[now].size(); for(int i=0;i<Size;i++) { ss e=edg[edges[now][i]]; if(e.flow>0&&dis[e.v]>dis[now]+e.cost) { dis[e.v]=dis[now]+e.cost; pre[e.v]=edges[now][i]; addflow[e.v]=min(addflow[now],e.flow); if(!vis[e.v]) { vis[e.v]=1; q.push(e.v); } } } } if(dis[t]==INF)return 0; flow+=(long long)addflow[t]; cost+=(long long)dis[t]*addflow[t]; int now=t; while(now!=s) { edg[pre[now]].flow-=addflow[t]; edg[pre[now]^1].flow+=addflow[t]; now=edg[pre[now]].u; } return 1; } void MCMF(int s,int t,long long &flow,long long &cost) { while(spfa(s,t,flow,cost)); } int main() { int t; int r[N]; int p,m,f,n,s; scanf("%d",&t); for(int i=1;i<=t;i++)scanf("%d",&r[i]); scanf("%d %d %d %d %d",&p,&m,&f,&n,&s); int S=2*t+1,T=2*t+2; for(int i=1;i<=t;i++) { addedge(S,2*i,r[i],0); addedge(2*i-1,T,r[i],0); addedge(S,2*i-1,INF,p); } for(int i=1;i<t;i++)addedge(2*i,2*(i+1),INF,0); for(int i=1;i<=t;i++) { if(i+m<=t)addedge(2*i,2*(i+m)-1,INF,f); if(i+n<=t)addedge(2*i,2*(i+n)-1,INF,s); } long long flow=0,cost=0; MCMF(S,T,flow,cost); printf("%lld\n",cost); return 0; }

