3. 二叉平衡树

标签：value   color   class   顺时针   如何   这一   查找   log   高度   

一、平衡二叉树是带有平衡条件的二叉查找树

平衡条件：平衡二叉树的每个结点的左子树和右子树的高度最多差1。

平衡因子 bf ：左子树的高度减去右子树的高度，显然 bf 的取值范围是 [ -1, 1 ] 。每一个结点（在其结点结构中）保留平衡因子 bf 。 

/* 平衡二叉树的结点结构 */ 
struct BinaryTreeNode {
	int bf;					// 平衡因子，当前结点的左右子树的高度差 
	int value;
	BinaryTreeNode *lChild;
	BinaryTreeNode *rChild;
}; 

补：虽然平衡二叉树能确保树的高度为O(logn)，但同时我们对其的插入/删除操作都需保持它的平衡条件。

二、旋转操作——保持平衡二叉树的平衡条件

1. 失衡的四种情况（把当前因失衡而必须重新平衡的结点叫做α）

• 对α的左儿子的左子树进行一次插入（左-左情况，以α为轴右旋）
• 对α的左儿子的右子树进行一次插入（左-右情况，先左旋，再右旋）
• 对α的右儿子的左子树进行一次插入（右-左情况，先右旋，再左旋）
• 对α的右儿子的右子树进行一次插入（右-右情况，以α为轴左旋）

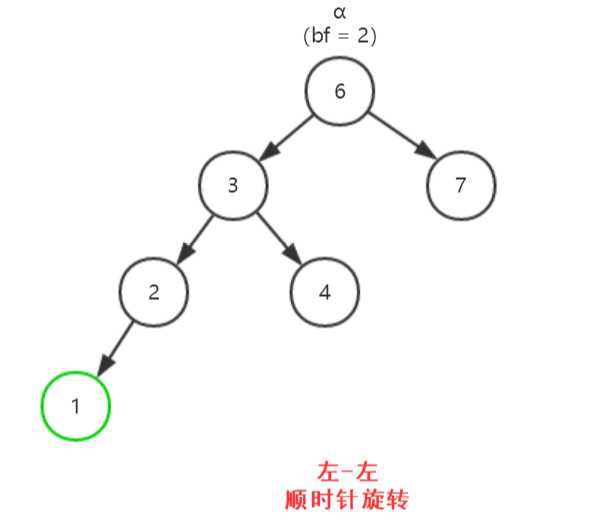
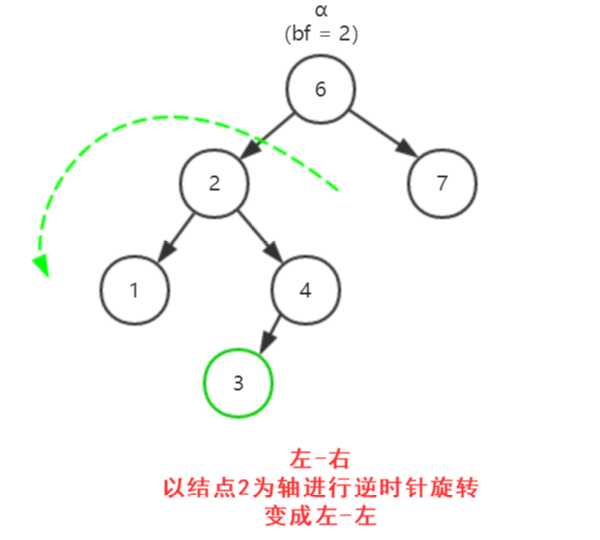
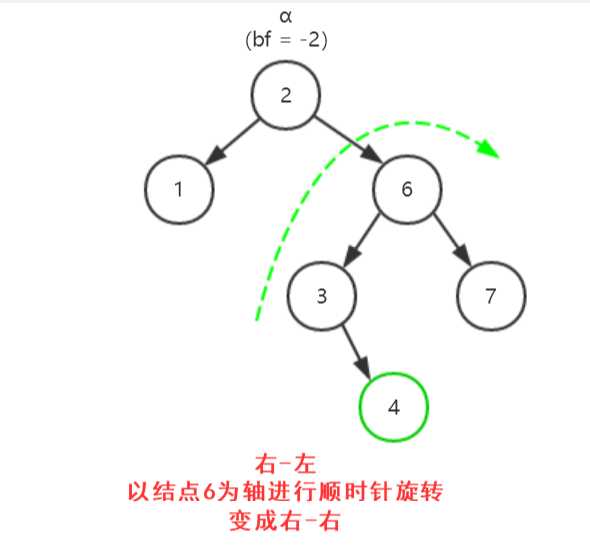
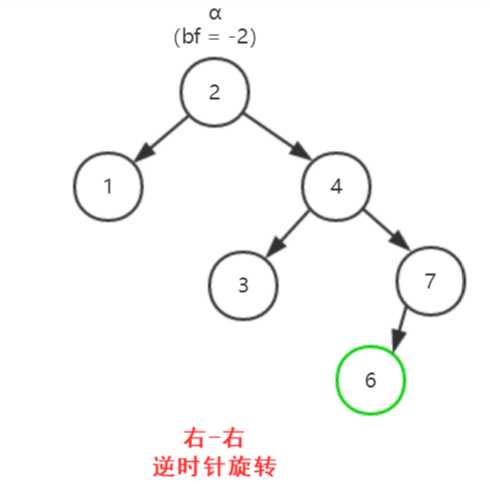
2. 示例

【左-右】（涉及的双旋结点为8、9、10）

（1）以8为轴进行左旋（逆时针旋转）

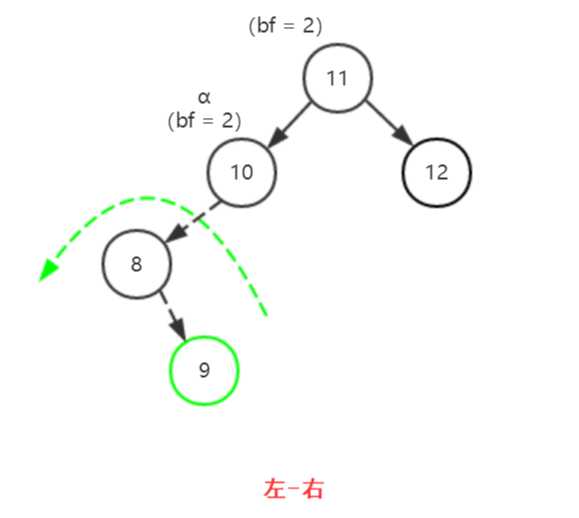
（2）以10为轴进行右旋（顺时针旋转）

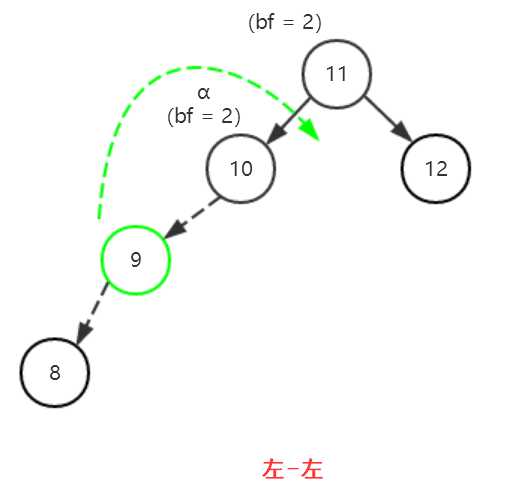
（3）得到平衡二叉树

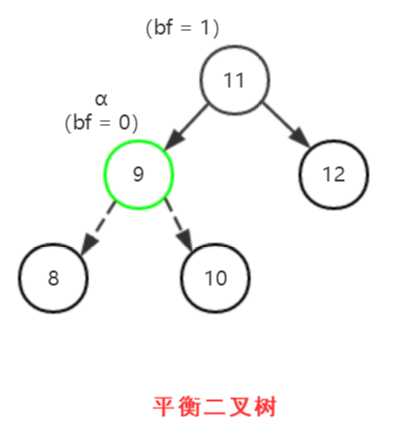
分析：当有多个结点的 | bf | > 1时，需要重新平衡的结点 α 是离新加入结点最近的。

【右-左】（涉及的双旋结点为7、15、16）

（1）以16为轴进行右旋（顺时针旋转）

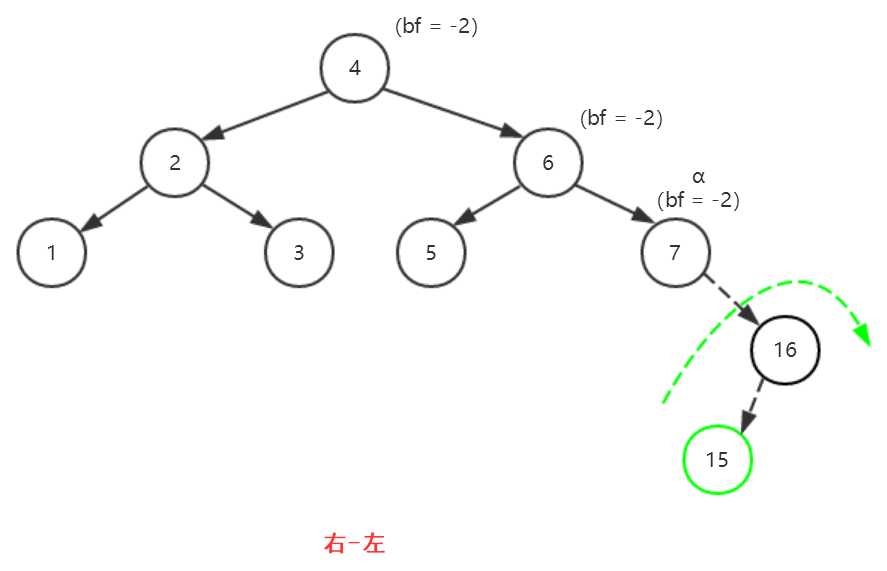
（2）以7为轴进行左旋（逆时针旋转）

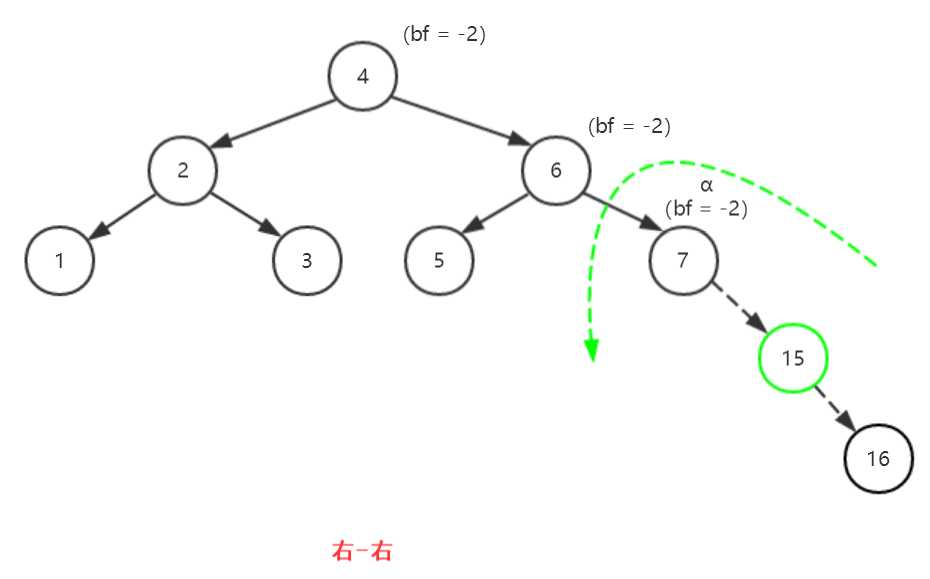
（3）得到平衡二叉树

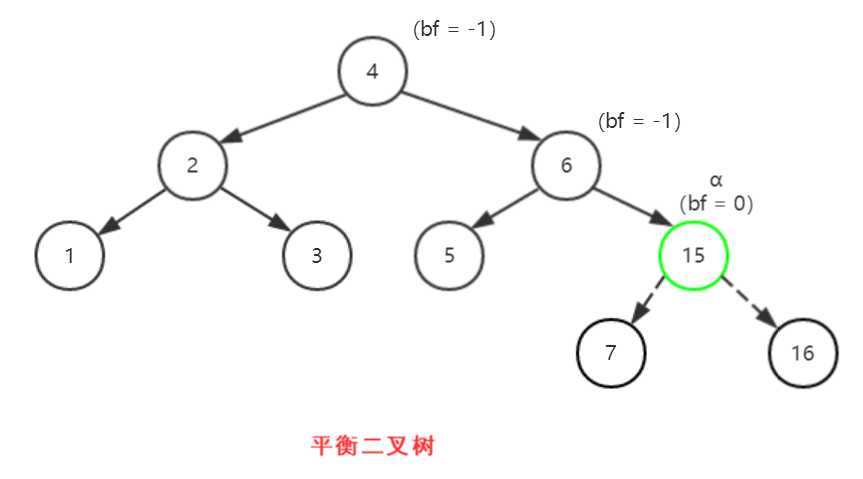
【右-左】涉及的双旋结点为6、7、15

（1）以15为轴进行右旋（顺时针旋转）

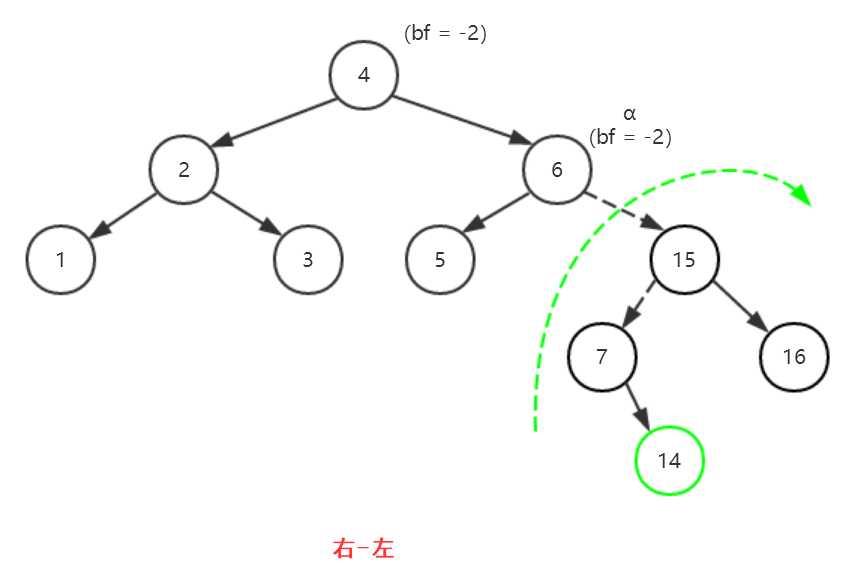
（2）以6为轴进行左旋（逆时针旋转）

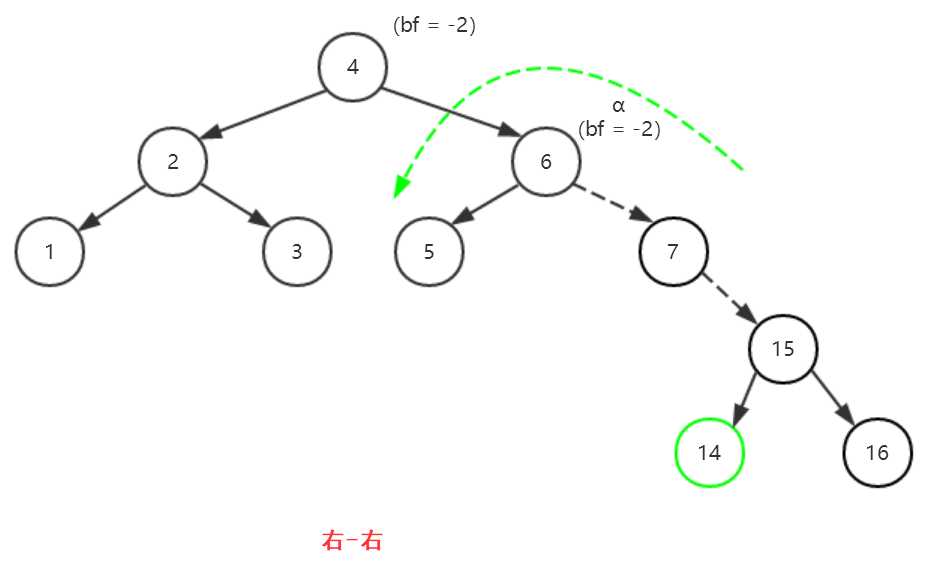
（3）得到平衡二叉树

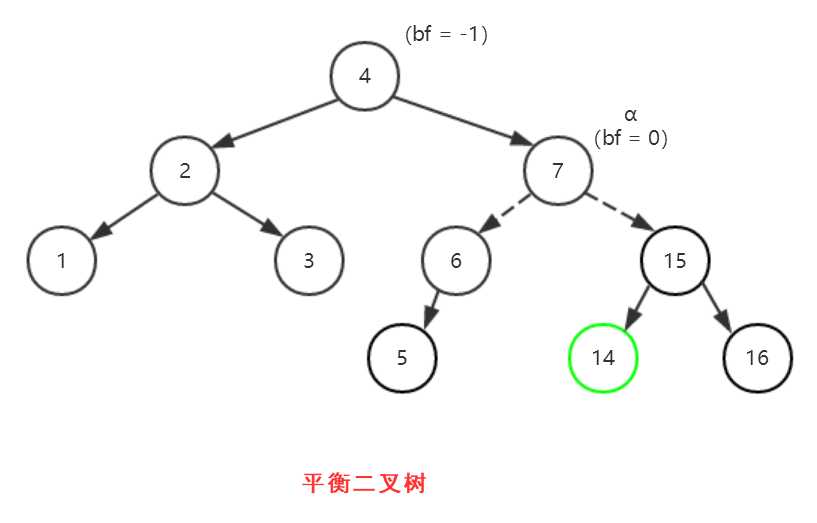
【小结：如何判断是哪种失衡情况】

结点α：离新加入结点最近的且| bf | > 1 的结点 。

以上图为例，结点α为6，然后再观察从结点α到新加入的结点14形成的路径“6-->15-->7-->14”，发现“6-->15-->7”形成的正是右-左这一情况。

3. 代码

3. 二叉平衡树

标签：value   color   class   顺时针   如何   这一   查找   log   高度   

原文地址：https://www.cnblogs.com/xzxl/p/9571521.html