标签:ons 4.6 最短路 论文 样本 graphx alt hash 自己
8. 过滤噪声边
在当前的伴生关系中,边的权重是基于一对概念同时出现在一篇论文中的频率来计算的。这种简单的权重机制的问题在于:它并没有对一对概念同时出现的原因加以区分,有时一对概念同时出现是由于它们具有某种值得我们关注的语义关系,但有时一对概念同时出现只是因为都频繁地出现在所有文档中,同时出现只是碰巧而已。我们需要使用一种新的权重机制,在给定概念在数据中的总体频繁度的情况下,它需要考虑给定的两个概念对于一个文档的“意义”或是“新颖度”。我们将使用皮尔逊卡方测试(Pearson’s chi-squared test)来严格计算这种“意义”,也就是说,我们要测试一个概念的出现与其他概念的出现是否是独立的。
对任何概念对 A 和 B,我们可以建立一个 2x2 的相关表,它包含了这两个概念同时出现在 MEDLINE 文档中的次数:
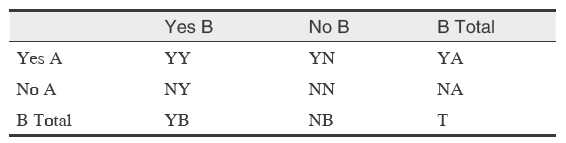
该表中 YY、YN、NY和NN 分别代表概念A和B在文档中 出现/没出现 的原始次数。T 是文档总数,YY + NY 为 B 出现在 T 中的总数,YN + NN 为 B 不出现在 T 中的总数,YB + NB为T。YY + YN 为A 出现在T 中的总数,NY + NN 为 A 不出现在 T 中的总数,YA + NA 为T。
卡方测试时,我们可以把 YY、YN、NY和 NN 看成某个未知分布的观测,可以根据这些值计算卡方统计量:
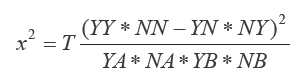
如果样本实际上是独立的,那么我们期望该统计量服从适当自由度的卡方分布。假定 r 和 c 是待比较的两个随机变量的基数,则自由度为 (r-1)(c-1)=1。卡方统计量大则表明随机变量相互独立的可能性小,因此两个概念同时出现是有意义的。更具体的讲,自由度为 1 的卡方分布的 CDF(累积分布函数)给出一个 p-value,它是我们拒绝变量是独立的这个被择假设的置信水平。下面我们使用GraphX来计算伴生图中每个概念对的卡方统计量。
1. 处理 EdgeTriplet
求卡方统计量时最简单的部分就是计算T,也就是需要考虑的文档的总个数,可以直接用 count方法获取:
val T = medline.count()
计算每个概念在多少篇文档中出现也相对简单,直接计算每个概念出现的次数即可:
scala> val topicCountsRdd = topics.map( x => (hashId(x), 1)).reduceByKey(_+_)
topicCounts: org.apache.spark.rdd.RDD[(Long, Int)] = ShuffledRDD[150] at reduceByKey at <console>:37
有了这个表示主题词出现次数的 VertexRDD,就可以将它作为顶点集合,再加上以后的 edges RDD 来创建一个新图:
val topicCountGraph = Graph(topicCountsRdd, topicGraph.edges)
计算卡方统计量,需要组合顶点数据(比如每个概念在一个文档中出现的次数)和边数据(比如两个概念同时出现在一个文档中的次数)。为了支持这种计算,GraphX 提供了一个数据结构EdgeTriplet[VD, ED],该数据结构将顶点和边的属性连同两个顶点的 ID 一起包装进一个对象。给定topicCountGraph 上的一个 EdgeTriplet,就能算出卡方统计量。首先定义计算卡方统计量的方法:
def chiSq(YY: Int, YB: Int, YA: Int, T: Long): Double = {
val NB = T - YB
val NA = T - YA
val YN = YA - YY
val NY = YB - YY
val NN = T - NY - YN - YY
val inner = (YY * NN - YN * NY) - T / 2.0
T * math.pow(inner, 2) / (YA * NA * YB * NB)
}
然后可以用该方法通过 mapTriplets 算子转换边的值。mapTriplets 算子返回一个新图,这个图的边的属性就是每个伴生对的卡方统计量。于是我们就可以大概知道该统计量在所有边上的分布情况:
val chiSquaredGraph = topicCountGraph.mapTriplets( triplet => {
chiSq(triplet.attr, triplet.srcAttr, triplet.dstAttr, T)
})
chiSquaredGraph.edges.map(x => x.attr).stats()
res10: org.apache.spark.util.StatCounter = (count: 213745, mean: 877.957047, stdev: 5094.935102, max: 198668.408387, min: 0.000000)
计算完卡方统计量,我们想用它去过滤那些没有意义的伴生概念对。从边的分布可以看出,数据中卡方统计量的范围很大,所以应该过滤掉更多的噪声边。对一个 2x2 的相关性表,如果变量没有相关性,我们期望卡方指标的值服从自由度为 1 的卡方分布。通过查阅自由度为 1 的卡方分布表,可以看到两个随机变量 99.999% 不相关的阈值为 10.83,也就是说:如果卡方统计量在大于 10.83 时,两个随机变量有 99.999% 的概率相关。
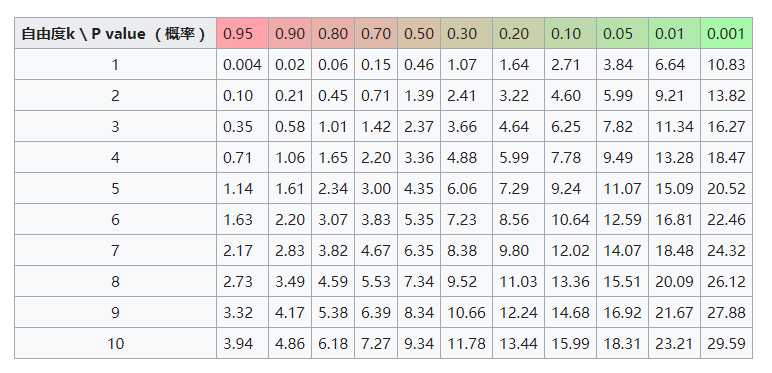
根据原书,我们仍使用 19.5 作为阈值,这样过滤后图中就只剩下那些置信度非常高的有意义的伴生关系。我们将在图上利用 subgraph 方法进行过滤,这个方法接受 EdgeTriplet 的一个布尔函数,用以判断子图应该包含哪些边:
> val interesting = chiSquaredGraph.subgraph( triplet => triplet.attr > 19.5)
interesting: org.apache.spark.graphx.Graph[Int,Double] = org.apache.spark.graphx.impl.GraphImpl@18484c41
> interesting.edges.count
res16: Long = 140575
采用以上规则,我们过滤掉了原始伴生关系图中约三分之一以上的边。该规则没有将更多的边过滤掉,这不是坏事,因为我们预期图中大多数伴生概念是语义相关,才因此同时出现的次数较多,而不是碰巧。
2. 去掉噪声边子图
我们在过滤后的子图上运行连通性算法:
> val interestingComponentCounts = sortedConnectedComponents(interesting.connectedComponents())
> interestingComponentCounts.size
res19: Int = 878
可以发现,在过滤掉接近三分之一左右的边后,连通组件总数并未发生改变。
> interestingComponentCounts.take(10).foreach(println)
(-9222594773437155629,13610)
(-6100368176168802285,5)
(-1043572360995334911,4)
(-8641732605581146616,3)
(-8082131391550700575,3)
(-5453294881507568143,3)
(-6561074051356379043,3)
(-2349070454956926968,3)
(-8186497770675508345,3)
(-858008184178714577,2)
且最大连通组件也并没有被瓦解。这说明图的连通结构对噪声边过滤有较好的鲁棒性。检查一下过滤后的度分布:
> val interestingDegrees = interesting.degrees.cache()
> interestingDegrees.map(_._2).stats()
res22: org.apache.spark.util.StatCounter = (count: 13721, mean: 20.490489, stdev: 29.864223, max: 863.000000, min: 1.000000)
原始分布为:(count: 13721, mean: 31.155892, stdev: 65.497591, max: 2596.000000, min: 1.000000)
可以看到,过滤后平均值变小了。但是更为人注意的是,最大度数下降了非常多,过滤前为 2596,过滤后为863。我们看一下过滤之后概念和度的关系:
scala> topNamesAndDegrees(interestingDegrees, topicGraph).foreach(println)
(Research,863)
(Disease,637)
(Pharmacology,509)
(Neoplasms,453)
(Toxicology,381)
(Metabolism,321)
(Drug Therapy,304)
(Blood,302)
(Public Policy,279)
(Social Change,277)
从结果来看,这次卡方过滤准则还比较理想:它在清楚对应普遍概念的边的同时,保留了代表概念之间有意义并且有值得注意的关系的那些边。我们可以继续用不同的卡方过滤准则进行试验,并且观察它们对图的连通性和度分布的影响。如果能找到卡方分布的某个值,并使用它作为过滤准则时,图中大型连通图组件开始瓦解,这种尝试会是很有意义的。
9. 小世界网络
现实生活中的图具有如下两个“小世界”属性:
对上述两个属性,小世界的提出者 “Watts“ 和 “Strogatz” 分别定义了一个指标。通过计算指标并和理想随机图的指标进行比较,我们可以测试概念网络是否具有小世界的属性。
1. cliques和聚类系数
如果每个顶点都存在一条边与其他任何节点都相连,那这个图就是个完全图。给定一个图,可能有多个子图是完全图,我们可以将这些子图称为派系(cliques)。如果途中存在这种许多大型的 cliques,表示这个图具有某种局部稠密结构,而真实的小世界网络也具有这种局部稠密结构。
不幸的是,在给定的图中寻找cliques 是非常困难的。判断一个图是否有给定大小的cliques
是一个NP-complete问题,也就是说,即使在一个小图里找cliques也是一个计算复杂度非常高的问题。
计算科学家提出了一些简单的指标,用于给出一个图里局部稠密性的情况,而不需要做大量的计算,在一个给定的途中找出所有 cliques。其中一个指标就是 triangle count(三角计数)。
三角形是一个完成图,顶点V的三角计数就是包含该顶点的三角形个数。三角计数度量了V有多少个邻接点是相互连接的。Watts 和 Strogatz 定义了一个新的指标,称为局部聚类系数,它是一个顶点的实际三角计数与其邻接点可能的三角级数的比率。对无向图来说,有 k 个邻接点和 t 个三角计数的顶点,其局部聚类系数C为:
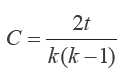
现在我们用 GraphX 来计算过滤后的概念图的每个节点的局部聚类系数。GraphX 有个内置方法 triangleCount,它返回一个 Graph 对象,其中 VertexRDD 包含了每个顶点的三角计数。
> val triCountGraph = interesting.triangleCount()
> triCountGraph.vertices.map(_._2).stats
res27: org.apache.spark.util.StatCounter = (count: 14548, mean: 74.660159, stdev: 295.327094, max: 11023.000000, min: 0.000000)
要计算局部聚类系数,我们需要通过每个顶点可能的三角计数对该顶点的三角形计数进行归一。每个顶点可能的三角计数可以从 degrees RDD 计算得出:
> val maxTrisGraph = interesting.degrees.mapValues( d => d * (d-1) / 2.0)
现在我们可以直接计算局部聚类系数(注意除 0 问题):
val clusterCoefGraph = triCountGraph.vertices.innerJoin(maxTrisGraph) { (vertexId, triCount, maxTris) => {
if (maxTris == 0) 0 else triCount / maxTris
}
}
然后对所有顶点局部聚类系数取平均值,就得到网络平均聚类系数:
> clusterCoefGraph.map(_._2).sum() / interesting.vertices.count()
res29: Double = 0.3062462560518856
2. 用Pregel计算平均路径长度
小世界网络的第二个属性就是任何两个节点之间的最短路径是较短的。这里我们会计算过滤之后的概念图中的大型连通组件节点的平均路径长度。
计算图中顶点之间的路径长度是一个迭代过程,和我们之前寻找连通组件的迭代过程类似:
这个在大规模分布式图上运行的以顶点为中心的迭代式并行计算方法,是基于谷歌的 Pregel。Pregel基于一个称为“批量同步并行”(BSP,Bulk-Synchronous Parallel)的分布式计算模型。BSP程序将并行处理阶段分成两个步骤:计算和通信。
在计算环节,图中每个顶点检查自己的内部状态并决定是否向图中其他节点发送消息。
在通信环节,Pregel框架负责将计算环节得到的消息路由到相应的顶点,目标顶点处理接收到的消息后更新自己的内部状态,并可能在下一个计算环节中产生新消息。计算和通信的过程会一直继续下去,直到图中所有顶点都一致投票同意停止运行,这时整个过程就结束了。
BSP 是最早的并行编程模型之一,它具有良好的通用性而且具有容错性,因此设计 BSP 系统时捕捉并保持任何计算阶段的系统状态是可能的。有了这些状态后,如果某台机器发生故障,就可以从其他机器上复制出发生故障的机器的状态,整个计算就可以回滚到故障发生前的状态,这样计算过程就可以继续下去。
GraphX 提供了表达BSP运算的内置pregel运算符,这个算子是以图为基础的。接下来我们会使用这个运算符来实现对一个图的平均路径长度的计算,这是一个迭代式的图并行计算,包括:
使用pregel实现分布式算法时需要确定三个问题。第一,要确定何种数据结构表示每个顶点状态和顶点之间传递的消息。对我们要解决的平均路径长度问题,我们希望每个顶点都有一个查询表,这个查询表包含当前顶点所知道的顶点的ID和它到这些顶点的距离。我们将为每个顶点建立一个Map[VertexId, Int] 并把这些信息存储在其中。类似的,发送给每个顶点的消息也应该有一个查询表,该表包含顶点ID和距离。这个距离是根据邻接点传递过来的信息计算出来的,同样可以用Map[VertexId, Int] 来表示这些信息。
确定了顶点状态和消息内容的数据结构后,我们可以实现两个函数。第一个函数是 mergeMaps,用于将新消息中的信息合并到顶点状态之中。对我们讨论的问题来说,顶点状态和消息都是 Map[VertexId, Int] 类型的,因此需要把两个 map 中的内容合并在一起并将每个 VertexId 关联到两个 map 中该 VertexId 对应两个条目的最小值。
标签:ons 4.6 最短路 论文 样本 graphx alt hash 自己
原文地址:https://www.cnblogs.com/zackstang/p/9570918.html