标签:关系 https cout oid 组合 cpp i++ display 构造
给出n,k求有多少个不大于n的三元组,使其中两两数字的和都是k的倍数,数字可以重复。
思考什么样的三个数可以满足这样的要求,当然这三个数都是k的倍数的时候是可以满足的,还有就是这三个数在d对k取模之后都等于k/2也应该是可以的。直接枚举这样的数就可以了。
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <iostream>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define MAXN 4000007
#define mo 19930726
#define ll long long
using namespace std;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
ll n,k,c1,c2;
int main()
{
cin>>n>>k;
for(re int i=1;i<=n;i++){
if(i%k==0) c1++;
}
if(k%2==0)
for(re int i=1;i<=n;i++){
if(i%k==k/2) c2++;
}
cout<<c1*c1*c1+c2*c2*c2;
}给出一个长度L,要求用不超过20个点,不超过60条边构造一张图,使其一共有L条1~N的路径,并且长度分别为0,1,2,...,L-1。允许有重边,且要求是拓扑图。
\[L\le 1000000\]
明显的一个构造题。入手点貌似不是很明显,考虑到\(1000000<2^{20}\),所以可以从二进制的方向入手。
不难发现的是,我们可以构造一条链,使编号相邻两个点之间都有一条边权为0的边,且从小到大构造长度为\(1,2,2^2,2^3,2^4...\)的边。这样路径长度就正好是0~\(2^n-1\)。但是当所求的数并不是2的某次方时是不行的,这个时候根据二进制位继续连边。
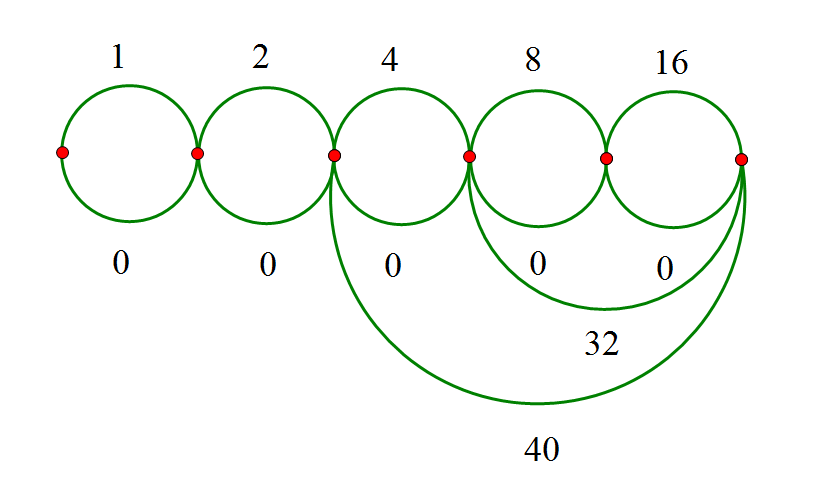
最多一共有19+19+18条共56条边,所以可以在题目要求范围内得出结果。
#include<bits/stdc++.h>
using namespace std;
struct po{
int x,y,dis;
}edge[100];
int num;
inline void add(int x,int y,int dis){
edge[++num].x=x;
edge[num].y=y;
edge[num].dis=dis;
}
int main()
{
int l,t;
cin>>l;
for(int i=0;i<21;i++) if(l&(1<<i)) t=i;
for(int i=1;i<=t-1;i++) add(i,i+1,1<<i-1),add(i,i+1,0);
add(t,20,0);
add(t,20,1<<t-1);
int g=1<<t;
while(g<l){
for(int i=0;i<21;i++) if((1<<i)&(l-g)) t=i;
add(t+1,20,g);
g|=1<<t;
}
cout<<"20 "<<num<<endl;
for(int i=1;i<=num;i++) cout<<edge[i].x<<" "<<edge[i].y<<" "<<edge[i].dis<<endl;
}有n个k面的骰子,求出所有\(i=2\)~\(2\times k\)中,满足任意两个骰子点数的和不等于i的方案数。
举个栗子:
当有三个三个面的骰子时(别管哪里来的三个面),输出为
7
7
4
7
7For i=2, the combinations (1,2,2),(1,2,3),(1,3,3),(2,2,2),(2,2,3),(2,3,3),(3,3,3) satisfy the condition, so the answer is 7.
For i=3, the combinations (1,1,1),(1,1,3),(1,3,3),(2,2,2),(2,2,3),(2,3,3),(3,3,3) satisfy the condition, so the answer is 7.
For i=4, the combinations (1,1,1),(1,1,2),(2,3,3),(3,3,3) satisfy the condition, so the answer is 4.
可以证明的是这个解答始终是对称的。
不难看出这个题应该是容斥,但是怎么容斥可能不是很容易想。可以先看看如果没有限制条件,我们一共可以有多少种方式。打表可以发现如果我们设\(g[i][j]\)为前i个球,最大的点数是j点,一共有多少种方法,那么\(g[i][j]=g[i-1][j]+g[i][j-1]\)。
可以从题目中确定,一组数据合不合法和数中的二元组有直接的关系,那么我们考虑固定某些二元组,然后让剩下的数组合,从而确定当这两个数不合法时的情况。
可以写出一个基础的容斥式子,如果我们用\(f[i]\)来表示一共有i组不和法的情况的方案数,那么
\[ans=\sum_{i=0}^{k/2}(-1)^if[i]\]
然后考虑\(f[i]\)应该怎么求,理智告诉我们,当我们固定了前i个二元组时,我们会剩下\(n-2\times i\)个数可供组合。那么不难得出:\(f[i]=C[k/2][i]*g[n-2*i][k]\)。
然后直接往上面那个公式里套,就可以得出正确的结果了。
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <queue>
#include <set>
#include <map>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define MAXN 4000007
#define mo 998244353
#define ll long long
using namespace std;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
ll f[4002][4002],g[2002][2002],b[5001],ans[4005],c[2005],n,k;
int main()
{
cin>>k>>n;
f[0][0]=1;
for(re int i=1;i<=k+n;i++){
f[i][0]=1;
for(re int j=1;j<=i;j++){
f[i][j]=(f[i-1][j-1]+f[i-1][j])%mo;
}
}
g[0][k]=1;
for(re int i=1;i<=k;i++) g[1][i]=i;
for(re int i=1;i<=n;i++) g[i][1]=1;
for(re int i=2;i<=n;i++)
for(re int j=2;j<=k;j++)
g[i][j]=(g[i-1][j]+g[i][j-1])%mo;
for(int i=1;i<=k;i++)
for(re int j=i;j<=k;j++)
b[i+j]++;
for(re int i=2;i<=2*k;i++){
for(re int j=0;j<=b[i]+(i%2==0?1:0)&&(j*2<=n);j++){
if(!(j&1)) ans[i]=(ans[i]+f[b[i]][j]*g[n-2*j][k]%mo)%mo;
else ans[i]=(ans[i]-f[b[i]][j]*g[n-2*j][k]%mo+mo)%mo;
}
}
for(re int i=2;i<=2*k;i++) cout<<ans[i]<<endl;
return 0;
}给出一个1~n的排列,你可以对这个排列进行一种操作,选择三个元素\(p_{i-1},p_i,p_{i+ 1}(2≤i≤N-1)\),使\(p_{i-1}>p_i>p_{i+ 1}\)然后翻转这三个元素的顺序。
求是否能使这个序列变成升序的。
这题出在acm赛制真的说不上多好,浓浓的瞎搞的气氛铺面而来。
首先我们可以确定元素的奇偶性和元素所在位置的奇偶性一定要是相同的,那个操作相当于隔着一个数交换两个数,所以怎么交换都不会改变一个数所在位置的奇偶性,那么如果一个偶数在一个奇数的位置上那就凉凉了。
接着判断还有什么不合法的情况,设\(pre[i]\)表示第i个数之前最大的数,\(nxt[i]\)表示第i个数之后最小的数,(均包括a[i])那么明显有一种不合法的情况就是$a[i]\not= i~and~nxt[i+1]<a[i]~and~pre[x-1]>a[i] $。
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <iostream>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define MAXN 4000007
#define mo 19930726
#define ll long long
using namespace std;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
int n,pre[MAXN],nxt[MAXN],a[MAXN],flag;
int main()
{
cin>>n;
for(re int i=1;i<=n;i++){
cin>>a[i];
if(a[i]%2!=i%2) flag=1;
}
for(re int i=1;i<=n;i++) pre[i]=max(pre[i-1],a[i]);
memset(nxt,100,sizeof(nxt));
for(re int i=n;i>=1;i--) nxt[i]=min(nxt[i+1],a[i]);
for(re int i=2;i<=n-1;i++)
if(a[i]!=i&&nxt[i+1]<a[i]&&pre[i-1]>a[i])
flag=1;
for(re int i=1;i<=n-1;i++)
if(((a[i]==i)==(a[i+1]==i+1))&&pre[i]!=i)
flag=1;
if(flag) cout<<"No";
else cout<<"Yes";
}标签:关系 https cout oid 组合 cpp i++ display 构造
原文地址:https://www.cnblogs.com/victorique/p/9575343.html