标签:区间 lower 分布 个数 int last type using 更改
前置知识:权值线段树。
主席树也就是可持久化线段树,它可以干嘛呢?我们看这样一道题目。
给定N个正整数构成的序列,将对于指定的闭区间查询其区间内的第K小值。
数据范围:\(1≤N,M≤2?10^5,-10^9≤a_i≤10^9\)
我们都知道权值线段树可以求全局第K大,但是不能求区间第K大,那遇到区间第K大如何处理呢?
区间?差分?对,我们可以用差分,权值线段树差分。
假设有这样一组数据
4 5
6 2 19 8
2 2 1
3 4 1
3 4 2
1 2 2
4 4 1
我们先离散,这是权值线段树基本操作把数列变为2,1,4,3看到有重复的也要去重。我们看图怎么实现:这是在线开点的线段树,所以儿子序号并不一定是父亲节点序号2或2+1

这是离散过后的权值线段树(空树),红色数字代表这区间有几个数。
我们开始加树进去,第一个数6,离散后是2,就把所有包含2的区间 个数+1,变成这样一张图。
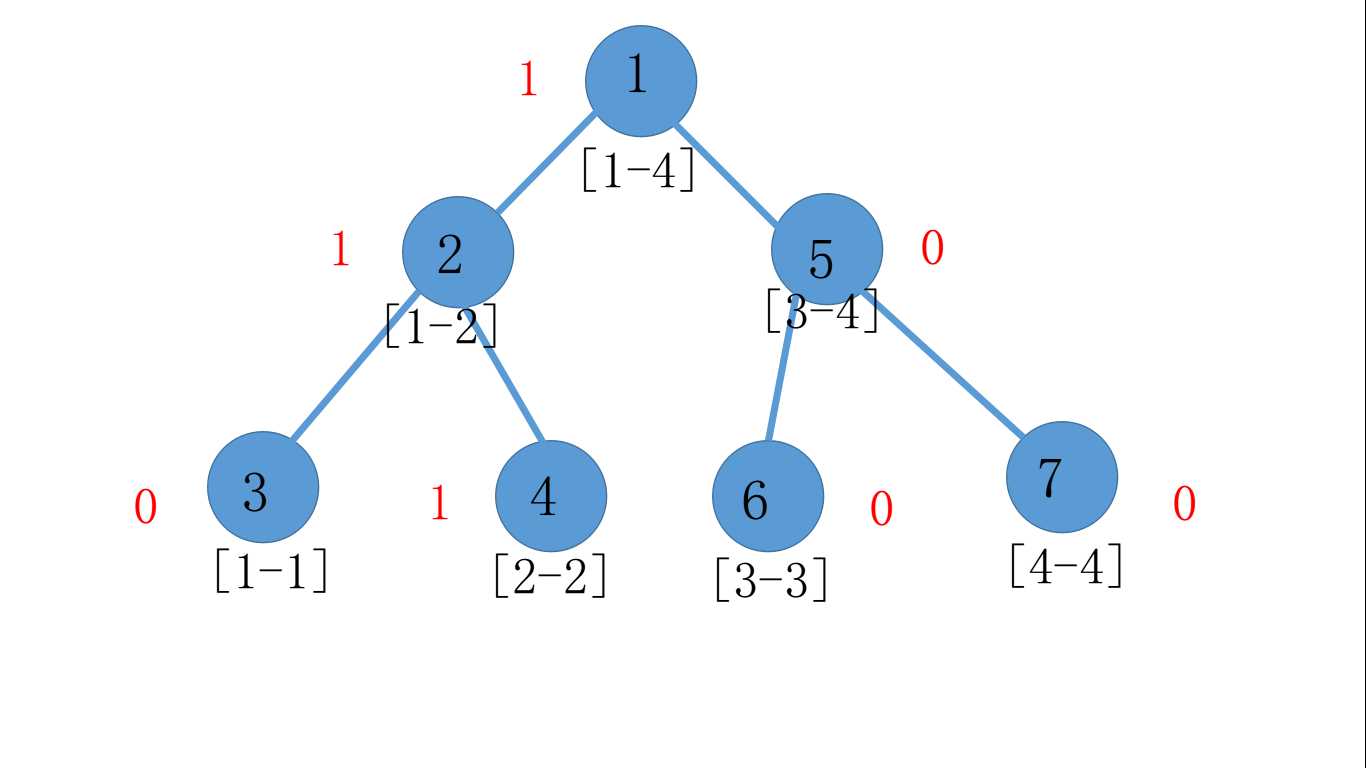
再加入2,离散后1,把所有包含1的区间个数+1.如图:

再加入19,离散后是4,把所有包含4的区间个数+1,如图:
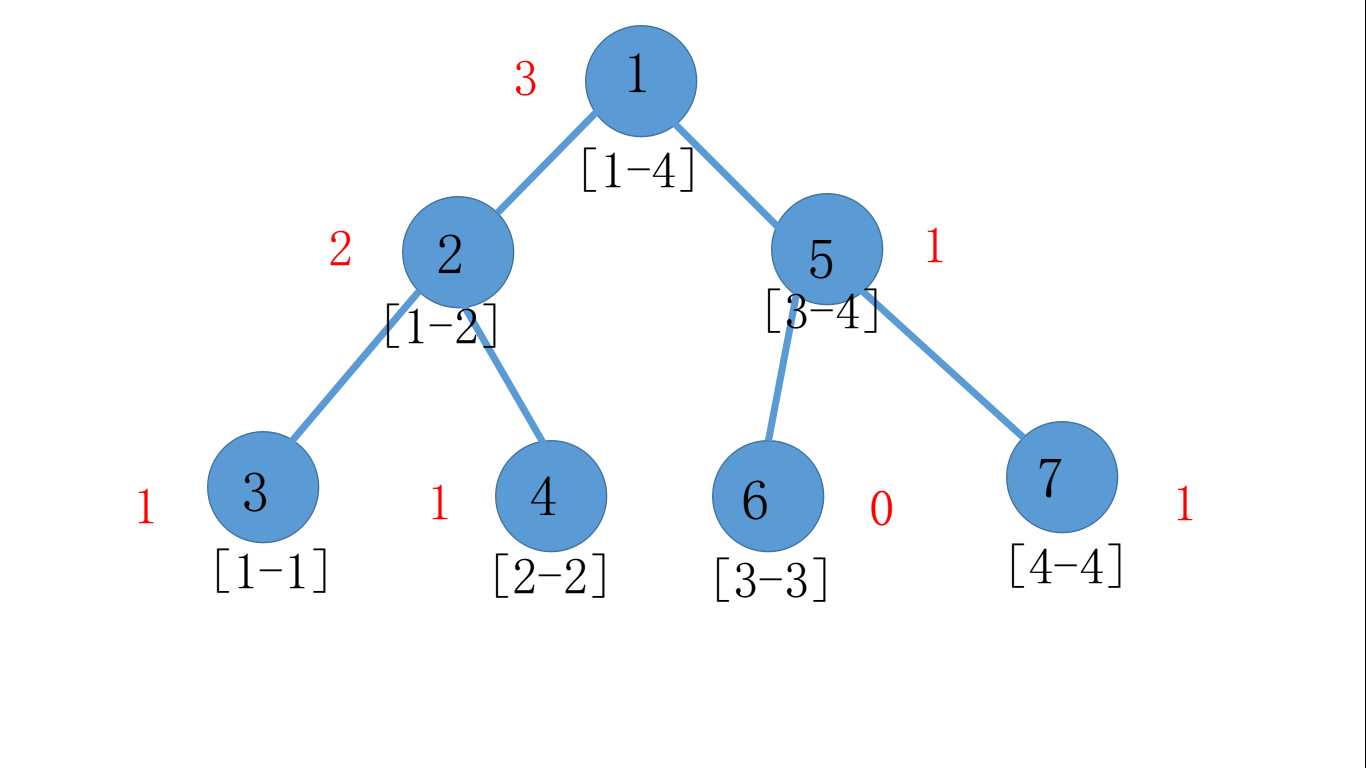
再加入8,离散后是3,把所有包含3的区间个数+1,如图:
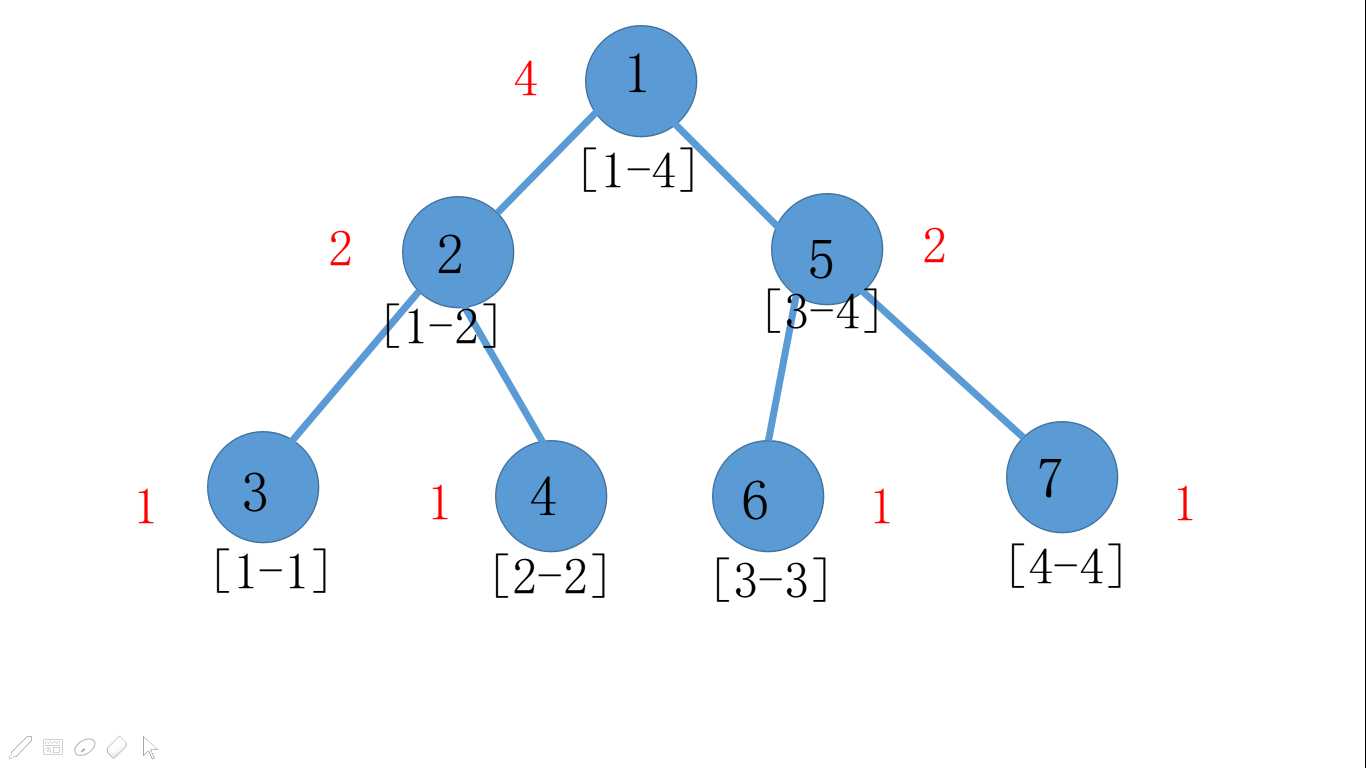
建完树了,我们每次开一颗线段树都记录下来,所以点的序号并不是我图中的序号*。这样我们得到了5颗线段树,假设看第一个询问2,2,1,我们只需要用第2颗线段树减去第1颗线段树这样就可以得到区间[2,2]的值分布情况接下来,就可以用权值线段树的方法,求区间第K大了。
但是我们可以发现,要建n颗线段树,那么空间复杂度变成\(n^2\),炸穿,需要优化。
容易发现,每次加入一个点,发现只会更改线段树上一条路上的值,其他的我们可以链上以前的点。空间复杂度\(nlogn\)。完美。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
using namespace std;
typedef long long ll;
ll a[2001000],hash[2010010],tot,root[2010010];
//root[],存下每一颗线段树的根
struct TREE
{
ll ln,rn,zhi;
}t[10010100];//ln左儿子,rn右儿子,zhi代表有多少个点在这个区间
void gai(ll &node,ll last,ll l,ll r,ll x)
{
node=++tot;//在线开点
t[node]=t[last];
t[node].zhi++;
if(l==r) return;
ll mid=(l+r)/2;
if(x<=mid) gai(t[node].ln,t[last].ln,l,mid,x);
else gai(t[node].rn,t[last].rn,mid+1,r,x);
}
ll cha(ll node,ll last,ll l,ll r,ll k)
{
if(l==r) return a[l];
ll p=t[t[node].ln].zhi-t[t[last].ln].zhi;//差分
ll mid=(l+r)/2;
if(k<=p) return cha(t[node].ln,t[last].ln,l,mid,k);
else return cha(t[node].rn,t[last].rn,mid+1,r,k-p);
}
int main()
{
ll n,m,x,y,k;
cin>>n>>m;
for(ll i=1;i<=n;i++)
scanf("%lld",&a[i]),hash[i]=a[i];
sort(a+1,a+1+n);
ll tt=unique(a+1,a+1+n)-a-1;//排序后,去重
for(ll i=1;i<=n;i++)
{
hash[i]=lower_bound(a+1,a+1+tt,hash[i])-a;//二分找出,这个点离散后的值。
gai(root[i],root[i-1],1,tt,hash[i]);//根据上一次得到的线段树,修改值。
}
for(ll i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&x,&y,&k);
printf("%lld\n",cha(root[y],root[x-1],1,tt,k));//差分
}
}其实主席树可以带修改,详细看我的另一篇博客。
题目链接
可持久化线段树(主席树模板)
可怜的狗狗
Count on a tree
Query on a tree III
标签:区间 lower 分布 个数 int last type using 更改
原文地址:https://www.cnblogs.com/kzj-pwq/p/9583099.html