标签:字典序 option code symbol word src clip jms time
Ancient Egyptians are known to have used a large set of symbols  to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words S1 and S2 of equal lengths on the wall of temple written one below the other. Since this temple is very ancient, some symbols from the words were erased. The symbols in the set
to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words S1 and S2 of equal lengths on the wall of temple written one below the other. Since this temple is very ancient, some symbols from the words were erased. The symbols in the set 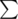 have equal probability for being in the position of any erased symbol.
have equal probability for being in the position of any erased symbol.
Fifa challenged Fafa to calculate the probability that S1 is lexicographically greater than S2. Can you help Fafa with this task?
You know that 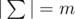 , i. e. there were m distinct characters in Egyptians‘ alphabet, in this problem these characters are denoted by integers from 1 to m in alphabet order. A word x is lexicographically greater than a word y of the same length, if the words are same up to some position, and then the word x has a larger character, than the word y.
, i. e. there were m distinct characters in Egyptians‘ alphabet, in this problem these characters are denoted by integers from 1 to m in alphabet order. A word x is lexicographically greater than a word y of the same length, if the words are same up to some position, and then the word x has a larger character, than the word y.
We can prove that the probability equals to some fraction 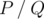 , where P and Q are coprime integers, and
, where P and Q are coprime integers, and 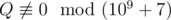 . Print as the answer the value
. Print as the answer the value 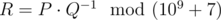 , i. e. such a non-negative integer less than 109?+?7, such that
, i. e. such a non-negative integer less than 109?+?7, such that 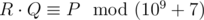 , where
, where 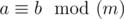 means that a and b give the same remainders when divided by m.
means that a and b give the same remainders when divided by m.
The first line contains two integers n and m (1?≤?n,??m?≤?105) — the length of each of the two words and the size of the alphabet 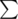 , respectively.
, respectively.
The second line contains n integers a1,?a2,?...,?an (0?≤?ai?≤?m) — the symbols of S1. If ai?=?0, then the symbol at position i was erased.
The third line contains n integers representing S2 with the same format as S1.
Print the value 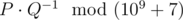 , where P and Q are coprime and
, where P and Q are coprime and 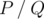 is the answer to the problem.
is the answer to the problem.
1 2
0
1
500000004
1 2
1
0
0
7 26
0 15 12 9 13 0 14
11 1 0 13 15 12 0
230769233
In the first sample, the first word can be converted into (1) or (2). The second option is the only one that will make it lexicographically larger than the second word. So, the answer to the problem will be 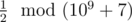 , that is 500000004, because
, that is 500000004, because 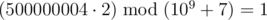 .
.
In the second example, there is no replacement for the zero in the second word that will make the first one lexicographically larger. So, the answer to the problem is 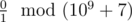 , that is 0.
, that is 0.
题意:给两个长度为n的数列,每个数列的数字范围是1-m,有可能出现缺失的部分(用0表示),在缺失的部分每个数字出现的概率相同(都是1/m),问最后a的字典序比b的大的概率.输入是 n,m 之后两行每行n个数,分别代表序列a,b.最后输出概率对1e9+7取模
提示:分数无法取模,所以要用逆元~另外要注意一下取模不然会爆
貌似有更简单的转移方式,只用一维就可以,也可以滚动数组写,但是我太弱了qwq
分几种情况讨论然后直接转移就行啦,这道题其实就是一个递推
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #define maxn 100010 5 #define mod 1000000007 6 #define ll long long 7 using namespace std; 8 int n,m; 9 int a[maxn],b[maxn]; 10 ll inv[maxn],f[maxn][2];//f[i][1]表示到i位为止,a>b的概率 11 ll fp(ll x,ll a){//在jms学到的神奇写法 12 ll ret=1; 13 for(x%=mod;a;a>>=1,x=x*x%mod) 14 if(a&1) ret=ret*x%mod; 15 return ret; 16 } 17 int main(){ 18 scanf("%d%d",&n,&m);//长度为n 字母表中有m个字母 19 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 20 for(int i=1;i<=n;i++) scanf("%d",&b[i]); 21 f[0][0]=1; 22 ll invm=fp(m,mod-2),inv2=fp(2,mod-2); 23 for(int i=1;i<=n;i++){ 24 if(a[i]>b[i]&&b[i]) //这一位都已经确定,直接转移即可 25 f[i][1]=(f[i-1][1]+f[i-1][0])%mod; 26 else if(a[i]<b[i]&&a[i]) 27 f[i][1]=f[i-1][1];//f[i][0]=0 28 else if(a[i]==b[i]&&a[i]) 29 f[i][1]=f[i-1][1],f[i][0]=f[i-1][0]%mod; 30 else if(!a[i]&&!b[i]){ 31 f[i][0]=f[i-1][0]*invm%mod; 32 f[i][1]=(f[i-1][1]+((f[i-1][0]*((1-invm)%mod+mod)%mod)%mod*inv2)%mod)%mod;//相等的概率是1/m,剩下的对半分 33 } 34 else if(!a[i]){ 35 f[i][0]=f[i-1][0]*invm%mod; 36 f[i][1]=(f[i-1][1]+(f[i-1][0]*(invm*((m-b[i])%mod+mod)%mod)%mod)%mod)%mod; 37 } 38 else if(!b[i]){ 39 f[i][0]=f[i-1][0]*invm%mod; 40 f[i][1]=(f[i-1][1]+(f[i-1][0]*(invm*((a[i]-1)%mod+mod)%mod)%mod)%mod+mod)%mod; 41 } 42 } 43 printf("%lld\n",(f[n][1]%mod+mod)%mod); 44 return 0; 45 }
CF935D Fafa and Ancient Alphabet 概率dp(递推)
标签:字典序 option code symbol word src clip jms time
原文地址:https://www.cnblogs.com/al76/p/9583478.html