标签:回溯 class 完全 还需 跳过 描述 回溯法 循环 parent
回溯法是暴力搜索法的一种,从直观的角度来看,它是建立了一颗树。但和完全的暴力法不同的是,它在求解的过程中能够对于那些不符合要求的节点及时的剪枝,“回溯”回去。
在建立这颗树的过程当中,控制好递归当中循环的细节、退出的条件、添加哪些节点的值是至关重要的。不同的方法得到的树不同,结果也不同。
下面是一些leetcode的题目,可以帮助更好的理解回溯法。
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
代码如下:
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
results = []
self.generate_helper(results, '', 0, 0, n)
return results
def generate_helper(self, results, str, open, close, max):
if len(str) == 2 * max:
results.append(str)
return
if open < max:
self.generate_helper(results, str+'(', open+1, close, max)
if close < open:
self.generate_helper(results, str+')', open, close+1, max)图片描述:

分析:递归的时候左括号总是在右括号前面,而且右括号的数量不得多于左括号,递归结束的条件是括号长度等于预定的长度。
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
? [7],
? [2,2,3]
]
示例2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
? [2,2,2,2],
? [2,3,3],
? [3,5]
]
代码如下:
class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
results = []
candidates.sort()
self.dfs(candidates, target, 0, [], results)
return results
def dfs(self, candidates, target, index, result, results):
if target < 0:
return
if target == 0:
results.append(result)
return
for i in range(index, len(candidates)):
self.dfs(candidates, target-candidates[i], i,result+[candidates[i]], results)
# 在这里使用result+[candidates[i]],而不是使用append。
# +产生了一个新的对象,而append是在原有的对象上面进行更新。
# 如果要使用append,那么当这一步运行完以后,还需要把添加的值pop出来(相当于回溯),
# 另外程序16行要修改为results.append(result.copy())。
# 我的程序均使用第一种方法。 图片描述:
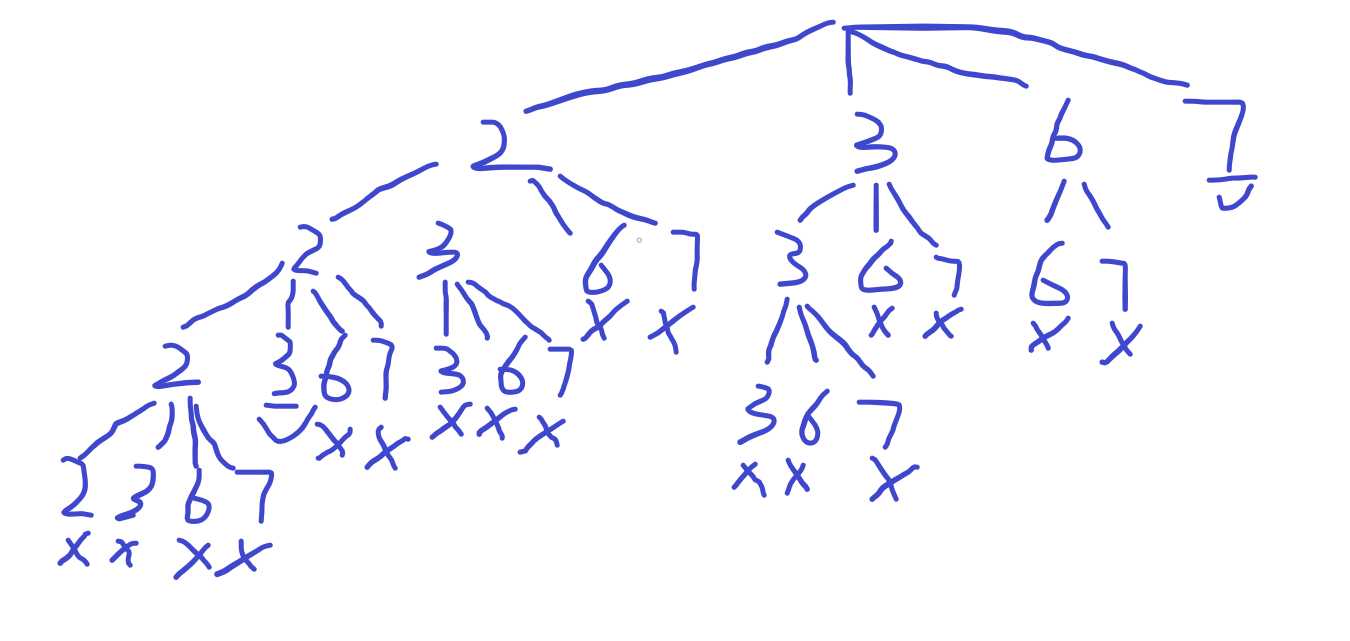
分析:树的左侧节点值明显要比右侧节点值多,也就是树向左偏,这是由递归过程中的for循环来决定的,确切的是由传入的i的值决定的。
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
? [1,7],
? [1, 2, 5],
? [2, 6],
? [1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
? [1,2,2],
? [5]
]
代码如下:
class Solution:
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
candidates.sort()
results = []
self.dfs(candidates, target, 0, [], results)
return results
def dfs(self, candidates, target, index, result, results):
if target <0:
return
if target == 0:
results.append(result)
return
for i in range(index, len(candidates)):
if i > index and candidates[i] == candidates[i-1]:
continue
self.dfs(candidates, target-candidates[i], i+1, result+[candidates[i]], results)图片描述:
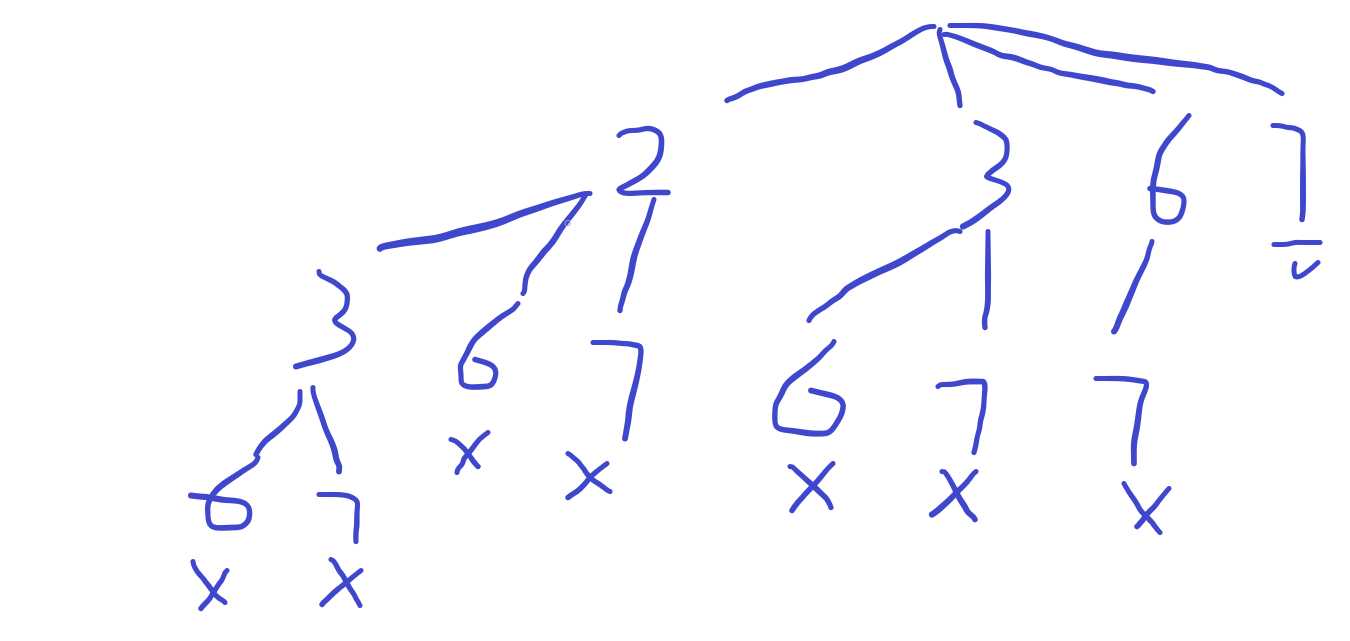
分析:可以看出和上一题相比,在递归循环的里面有两个不同,第一个不同是:使用continue来处理重复值的情况,当第二次出现的值和第一次出现的值相同的时候,由于在第一次已经处理过了,所有以后会直接跳过。另外一点不同的是递归传入的值由i变成了i+1,这可以在两张图里面看出来,比如第一张图2下面的节点是2,3,6,7,而第二张图的节点是3,6,7,是因为i的值多增加一位的缘故。
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
? [1,2,3],
? [1,3,2],
? [2,1,3],
? [2,3,1],
? [3,1,2],
? [3,2,1]
]
代码如下:
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
results = []
self.dfs(nums, [], results)
return results
def dfs(self, nums, result, results):
if len(nums) == 0:
results.append(result)
return
for i in range(len(nums)):
self.dfs(nums[:i]+nums[i+1:], result+[nums[i]], results)图片描述:
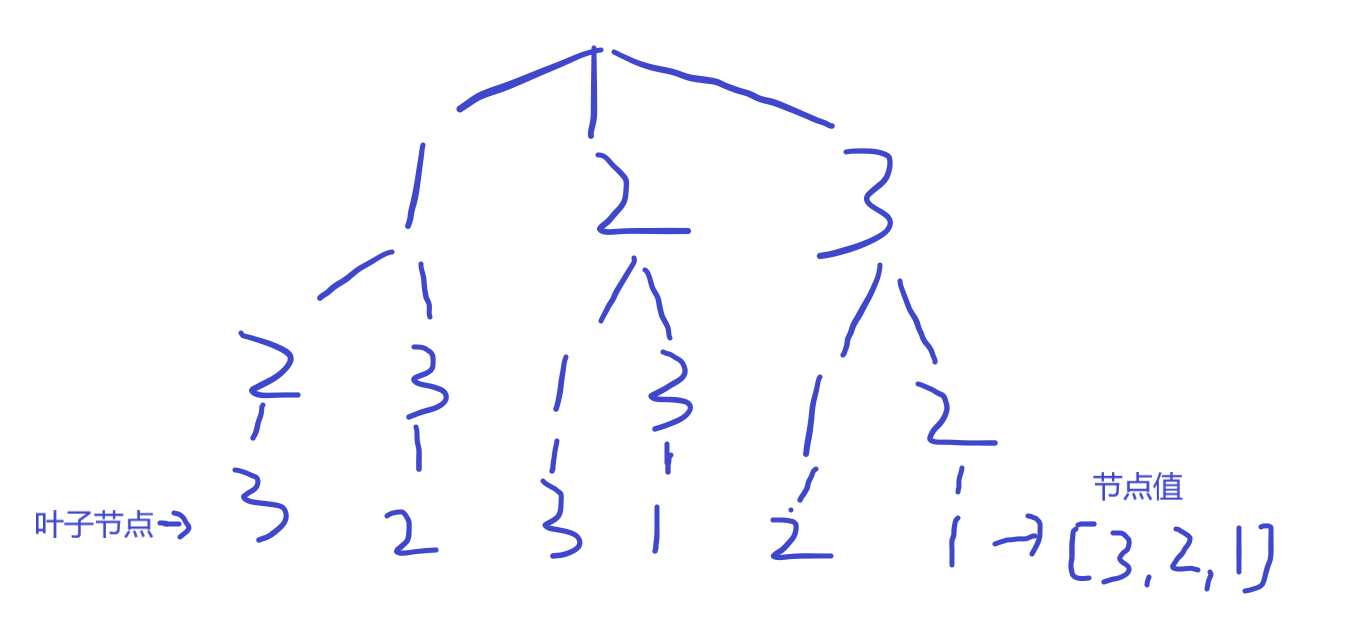
分析:树的左侧节点和右侧节点的值一样多,保存的是树的叶子节点的值。
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
? [1,1,2],
? [1,2,1],
? [2,1,1]
]
代码如下:
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
results = []
nums.sort()
self.dfs(nums, [], results)
return results
def dfs(self, nums, result, results):
if len(nums) == 0:
results.append(result)
return
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i-1]:
continue
self.dfs(nums[:i]+nums[i+1:], result+[nums[i]], results)给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
? [3],
? [1],
? [2],
? [1,2,3],
? [1,3],
? [2,3],
? [1,2],
? []
]
代码:
class Solution:
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
results = []
self.dfs(nums, 0, [], results)
return results
def dfs(self, nums, index, result, results):
if index == len(nums):
results.append(result)
return
results.append(result)
for i in range(index, len(nums)):
self.dfs(nums, i+1, result+[nums[i]], results)图片描述:
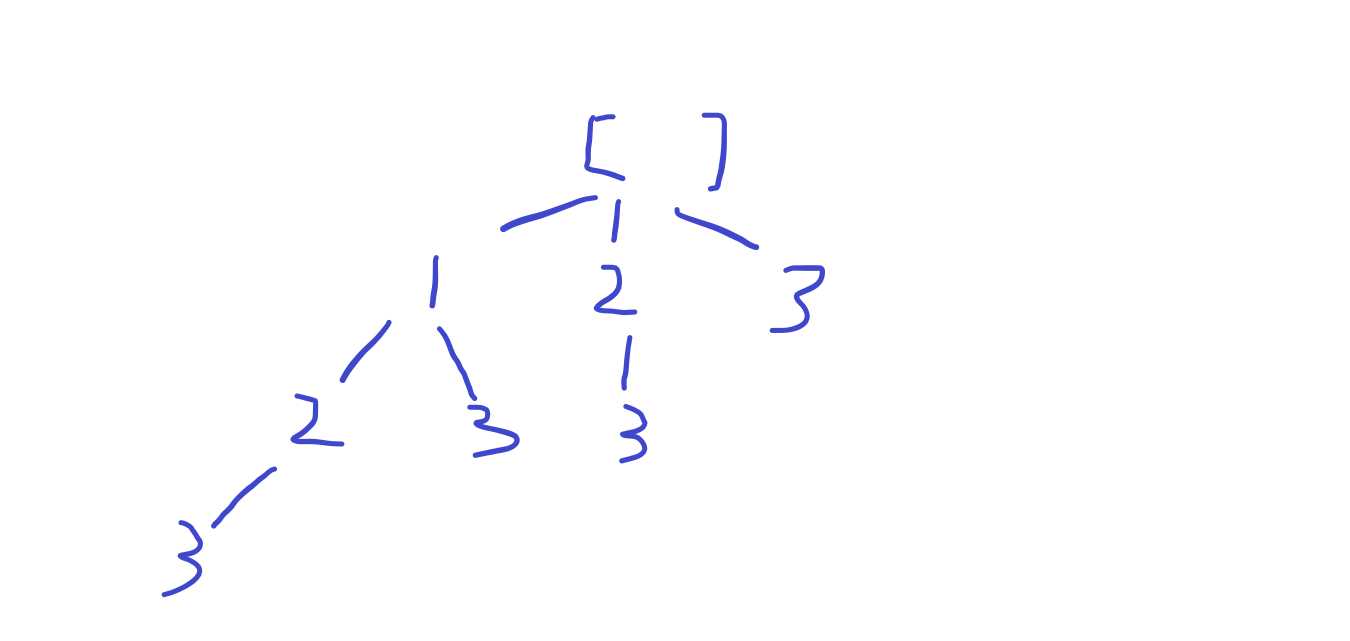
分析:在这道题当中,results当中保存所有节点的值,而不仅仅是叶子节点的值。
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
? [2],
? [1],
? [1,2,2],
? [2,2],
? [1,2],
? []
]
代码如下:
class Solution:
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums.sort()
results = []
self.dfs(nums, 0, [], results)
return results
def dfs(self, nums, index, result, results):
if index == len(nums):
results.append(result)
return
results.append(result)
for i in range(index, len(nums)):
if i > index and nums[i] == nums[i-1]:
continue
self.dfs(nums, i+1, result+[nums[i]], results)分析:和上一道题不同之处在于使用continue机制来处理重复的值。
标签:回溯 class 完全 还需 跳过 描述 回溯法 循环 parent
原文地址:https://www.cnblogs.com/jiaxin359/p/9588827.html