标签:sync lag name pre class com || 自己 check
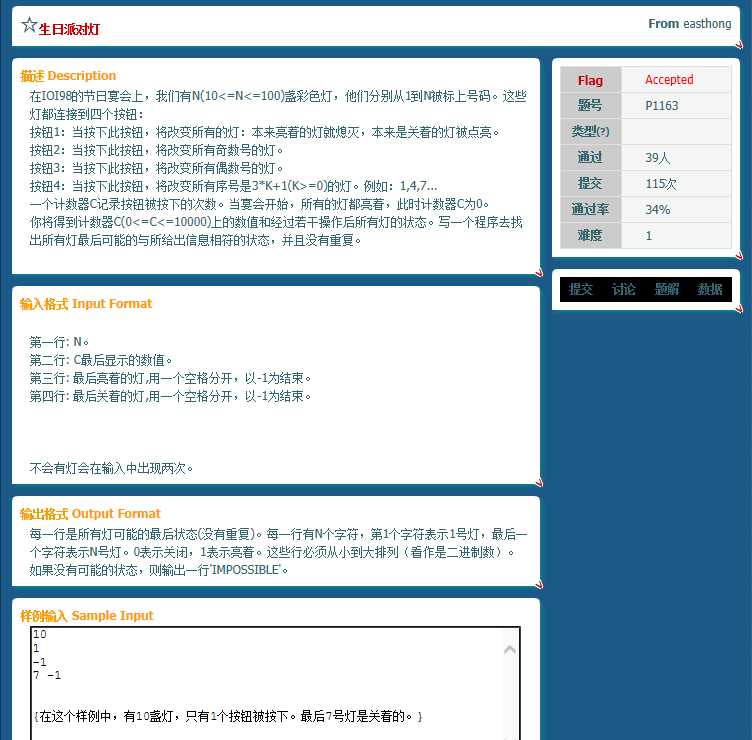
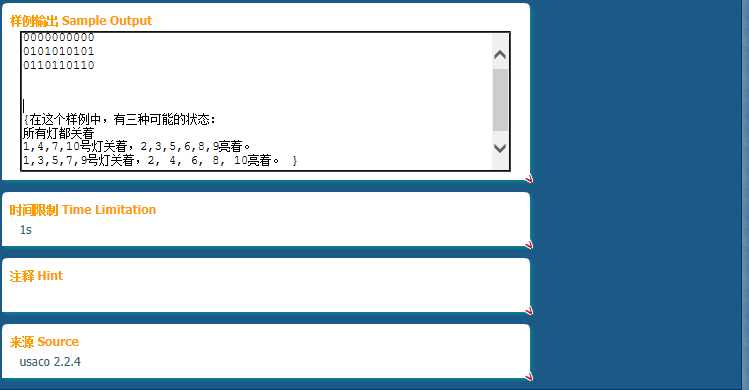
这个状态压缩还是好看出来的吧?后三个操作决定了所有的状态都是六个六个一循环的。
然后怎么写呢?书上说完压缩之后就不谈了,说让自己写搜索??这咋搜啊,还不是4^C?总之我是不会的。
今天又下定决心来看这题,发现和前几天做的动态规划很像,转移方程如下
if(flag[i-1][a[1]][a[2]][a[3]][a[4]][a[5]][a[6]]) { flag[i][!a[1]][!a[2]][!a[3]][!a[4]][!a[5]][!a[6]]=1; flag[i][!a[1]][a[2]][!a[3]][a[4]][!a[5]][a[6]]=1; flag[i][a[1]][!a[2]][a[3]][!a[4]][a[5]][!a[6]]=1; flag[i][!a[1]][a[2]][a[3]][!a[4]][a[5]][a[6]]=1; }
初状态是flag[0][1][1][1][1][1][1]=1。
那么这题就七重循环搞一搞就好了。
using namespace std; int i,f,t; int n,sum; int flag[10010][2][2][2][2][2][2],o[7],a[7];//777777777 bool check() { for(i=0;i<6;i++) if(o[i]==-1&&a[i]==1||o[i]==1&&a[i]==0) return 0; return 1; } int main() { ios::sync_with_stdio(false); //freopen("123.in","r",stdin); //freopen("123.out","w",stdout); cin>>n>>sum; for(cin>>t;t!=-1;cin>>t)//输入 o[t%6]=1; for(cin>>t;t!=-1;cin>>t) o[t%6]=-1; flag[0][1][1][1][1][1][1]=1; for(i=1;i<=sum;i++) for(a[1]=0;a[1]<=1;a[1]++) for(a[2]=0;a[2]<=1;a[2]++) for(a[3]=0;a[3]<=1;a[3]++) for(a[4]=0;a[4]<=1;a[4]++) for(a[5]=0;a[5]<=1;a[5]++) for(a[6]=0;a[6]<=1;a[6]++) if(flag[i-1][a[1]][a[2]][a[3]][a[4]][a[5]][a[6]])//转移 { flag[i][!a[1]][!a[2]][!a[3]][!a[4]][!a[5]][!a[6]]=1; flag[i][!a[1]][a[2]][!a[3]][a[4]][!a[5]][a[6]]=1; flag[i][a[1]][!a[2]][a[3]][!a[4]][a[5]][!a[6]]=1; flag[i][!a[1]][a[2]][a[3]][!a[4]][a[5]][a[6]]=1; } for(a[1]=0;a[1]<=1;a[1]++)//输出 for(a[2]=0;a[2]<=1;a[2]++) for(a[3]=0;a[3]<=1;a[3]++) for(a[4]=0;a[4]<=1;a[4]++) for(a[5]=0;a[5]<=1;a[5]++) for(a[6]=0;a[6]<=1;a[6]++) if(flag[sum][a[1]][a[2]][a[3]][a[4]][a[5]][a[6]]) { a[0]=a[6]; if(check()) { for(f=1;f<=n;f++) cout<<a[f%6]; cout<<endl; } } if(f==0)//我用f输出,其他的活都让i干。如果f还是0就说明没有输出过。论全局变量的妙用 cout<<"IMPOSSIBLE"; }
看起来七重循环怪吓人,但转移花费是C*2^6,肯定能跑完。
标签:sync lag name pre class com || 自己 check
原文地址:https://www.cnblogs.com/qywyt/p/9593734.html