标签:pandas dex 相关 样本 RKE marker 2.4 ima 默认
‘‘‘ 【课程1.7】 相关性分析 分析连续变量之间的线性相关程度的强弱 图示初判 / Pearson相关系数(皮尔逊相关系数) / Sperman秩相关系数(斯皮尔曼相关系数) ‘‘‘
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy import stats % matplotlib inline
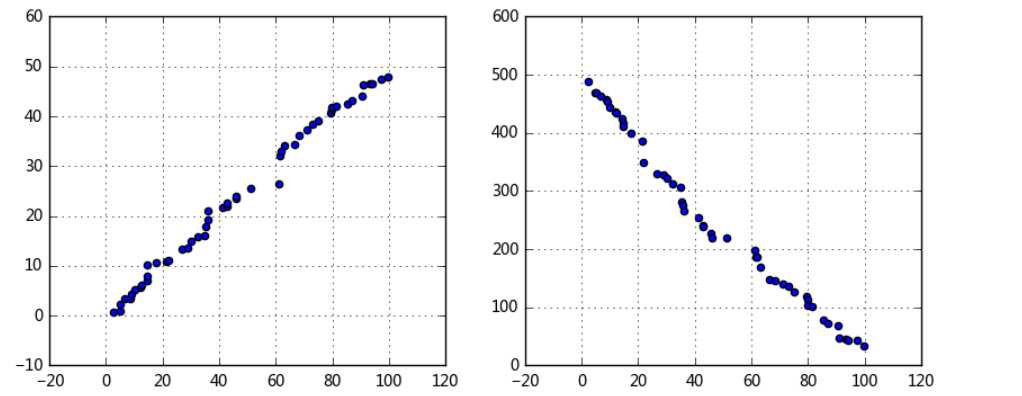
# 图示初判 # (1)变量之间的线性相关性 data1 = pd.Series(np.random.rand(50)*100).sort_values() data2 = pd.Series(np.random.rand(50)*50).sort_values() data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False) # 创建三个数据:data1为0-100的随机数并从小到大排列,data2为0-50的随机数并从小到大排列,data3为0-500的随机数并从大到小排列, fig = plt.figure(figsize = (10,4)) ax1 = fig.add_subplot(1,2,1) ax1.scatter(data1, data2) plt.grid() # 正线性相关 ax2 = fig.add_subplot(1,2,2) ax2.scatter(data1, data3) plt.grid() # 负线性相关
输出:
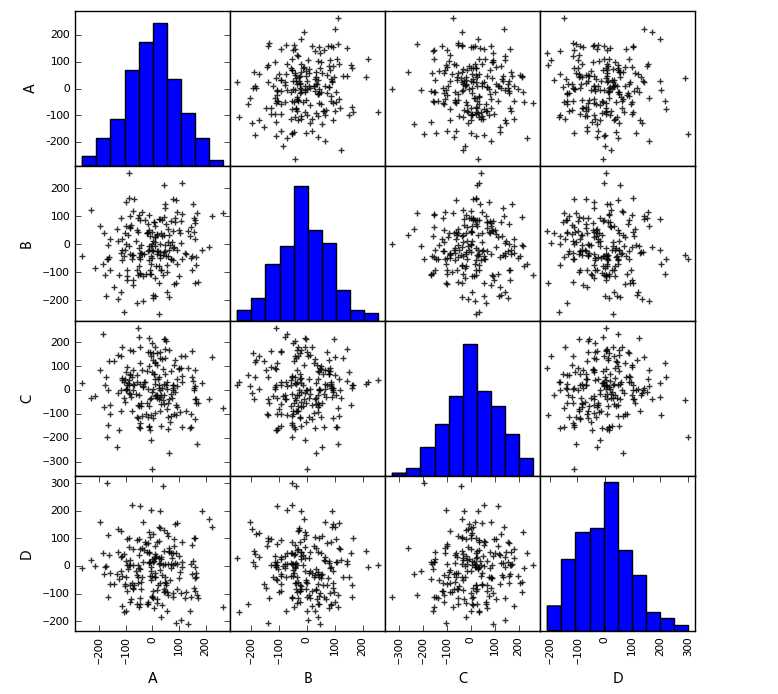
# 图示初判 # (2)散点图矩阵初判多变量间关系 data = pd.DataFrame(np.random.randn(200,4)*100, columns = [‘A‘,‘B‘,‘C‘,‘D‘]) pd.scatter_matrix(data,figsize=(8,8), c = ‘k‘, marker = ‘+‘, diagonal=‘hist‘, alpha = 0.8, range_padding=0.1) data.head()
输出:
A B C D 0 -100.107196 151.774404 75.914739 -40.279130 1 -45.713333 -29.882627 182.479549 61.600886 2 -4.293934 -68.730078 -102.025975 202.510936 3 55.385126 -171.545669 4.908165 120.779550 4 -72.515302 118.986304 0.212236 61.995667
# Pearson相关系数 data1 = pd.Series(np.random.rand(100)*100).sort_values() data2 = pd.Series(np.random.rand(100)*50).sort_values() data = pd.DataFrame({‘value1‘:data1.values, ‘value2‘:data2.values}) print(data.head()) print(‘------‘) # 创建样本数据 u1,u2 = data[‘value1‘].mean(),data[‘value2‘].mean() # 计算均值 std1,std2 = data[‘value1‘].std(),data[‘value2‘].std() # 计算标准差 print(‘value1正态性检验:\n‘,stats.kstest(data[‘value1‘], ‘norm‘, (u1, std1))) print(‘value2正态性检验:\n‘,stats.kstest(data[‘value2‘], ‘norm‘, (u2, std2))) print(‘------‘) # 正态性检验 → pvalue >0.05 data[‘(x-u1)*(y-u2)‘] = (data[‘value1‘] - u1) * (data[‘value2‘] - u2) data[‘(x-u1)**2‘] = (data[‘value1‘] - u1)**2 data[‘(y-u2)**2‘] = (data[‘value2‘] - u2)**2 print(data.head()) print(‘------‘) # 制作Pearson相关系数求值表 r = data[‘(x-u1)*(y-u2)‘].sum() / (np.sqrt(data[‘(x-u1)**2‘].sum() * data[‘(y-u2)**2‘].sum())) print(‘Pearson相关系数为:%.4f‘ % r) # 求出r # |r| > 0.8 → 高度线性相关
输出:
value1 value2 0 0.438122 1.055646 1 1.505379 1.515092 2 1.508023 2.323125 3 1.832305 3.552254 4 3.406128 4.155919 ------ value1正态性检验: KstestResult(statistic=0.095884626585008847, pvalue=0.29839852339800688) value2正态性检验: KstestResult(statistic=0.080469682048596169, pvalue=0.51965015851411267) ------ value1 value2 (x-u1)*(y-u2) (x-u1)**2 (y-u2)**2 0 0.438122 1.055646 1292.819837 2814.467243 593.854178 1 1.505379 1.515092 1242.927702 2702.366975 571.672643 2 1.508023 2.323125 1200.861611 2702.092121 533.685953 3 1.832305 3.552254 1129.876614 2668.483878 478.406924 4 3.406128 4.155919 1065.219453 2508.361644 452.363990 ------ Pearson相关系数为:0.9968
# Pearson相关系数 - 算法 data1 = pd.Series(np.random.rand(100)*100).sort_values() data2 = pd.Series(np.random.rand(100)*50).sort_values() data = pd.DataFrame({‘value1‘:data1.values, ‘value2‘:data2.values}) print(data.head()) print(‘------‘) # 创建样本数据 data.corr() # pandas相关性方法:data.corr(method=‘pearson‘, min_periods=1) → 直接给出数据字段的相关系数矩阵 # method默认pearson
输出:
value1 value2 0 1.037320 0.379353 1 2.098395 0.442863 2 3.926912 1.104473 3 4.427697 1.184688 4 5.528188 1.213196 ------ value1 value2 value1 1.000000 0.969122 value2 0.969122 1.000000
# Sperman秩相关系数 data = pd.DataFrame({‘智商‘:[106,86,100,101,99,103,97,113,112,110], ‘每周看电视小时数‘:[7,0,27,50,28,29,20,12,6,17]}) print(data) print(‘------‘) # 创建样本数据 data.sort_values(‘智商‘, inplace=True) data[‘range1‘] = np.arange(1,len(data)+1) data.sort_values(‘每周看电视小时数‘, inplace=True) data[‘range2‘] = np.arange(1,len(data)+1) print(data) print(‘------‘) # “智商”、“每周看电视小时数”重新按照从小到大排序,并设定秩次index data[‘d‘] = data[‘range1‘] - data[‘range2‘] data[‘d2‘] = data[‘d‘]**2 print(data) print(‘------‘) # 求出di,di2 n = len(data) rs = 1 - 6 * (data[‘d2‘].sum()) / (n * (n**2 - 1)) print(‘Pearson相关系数为:%.4f‘ % rs) # 求出rs
输出:
智商 每周看电视小时数 0 106 7 1 86 0 2 100 27 3 101 50 4 99 28 5 103 29 6 97 20 7 113 12 8 112 6 9 110 17 ------ 智商 每周看电视小时数 range1 range2 1 86 0 1 1 8 112 6 9 2 0 106 7 7 3 7 113 12 10 4 9 110 17 8 5 6 97 20 2 6 2 100 27 4 7 4 99 28 3 8 5 103 29 6 9 3 101 50 5 10 ------ 智商 每周看电视小时数 range1 range2 d d2 1 86 0 1 1 0 0 8 112 6 9 2 7 49 0 106 7 7 3 4 16 7 113 12 10 4 6 36 9 110 17 8 5 3 9 6 97 20 2 6 -4 16 2 100 27 4 7 -3 9 4 99 28 3 8 -5 25 5 103 29 6 9 -3 9 3 101 50 5 10 -5 25 ------ Pearson相关系数为:-0.1758
# Pearson相关系数 - 算法 data = pd.DataFrame({‘智商‘:[106,86,100,101,99,103,97,113,112,110], ‘每周看电视小时数‘:[7,0,27,50,28,29,20,12,6,17]}) print(data) print(‘------‘) # 创建样本数据 data.corr(method=‘spearman‘) # pandas相关性方法:data.corr(method=‘pearson‘, min_periods=1) → 直接给出数据字段的相关系数矩阵 # method默认pearson
输出:
智商 每周看电视小时数 0 106 7 1 86 0 2 100 27 3 101 50 4 99 28 5 103 29 6 97 20 7 113 12 8 112 6 9 110 17 ------ 智商 每周看电视小时数 智商 1.000000 -0.175758 每周看电视小时数 -0.175758 1.000000
标签:pandas dex 相关 样本 RKE marker 2.4 ima 默认
原文地址:https://www.cnblogs.com/654321cc/p/9595555.html