标签:蓝色 列操作 包括 决定 img back 分享 bubuko 平衡二叉查找树
红黑树(Red Black Tree) 是一种自平衡二叉查找树 :
l 每个节点或者是黑色,或者是红色。
l 根节点是黑色。
l 每个叶子节点是黑色。
l 如果一个节点是红色的,则它的子节点必须是黑色的。
l 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
红黑树的各种操作的时间复杂度是O(log2N)。
红黑树 vs AVL
红黑树的查询性能略微逊色于AVL树,因为他比avl树会稍微不平衡最多一层,也就是说红黑树的查询性能只比相同内容的avl树最多多一次比较,但是,红黑树在插入和删除上完爆avl树,avl树每次插入删除会进行大量的平衡度计算,而红黑树为了维持红黑性质所做的红黑变换和旋转的开销,相较于avl树为了维持平衡的开销要小得多
插入操作
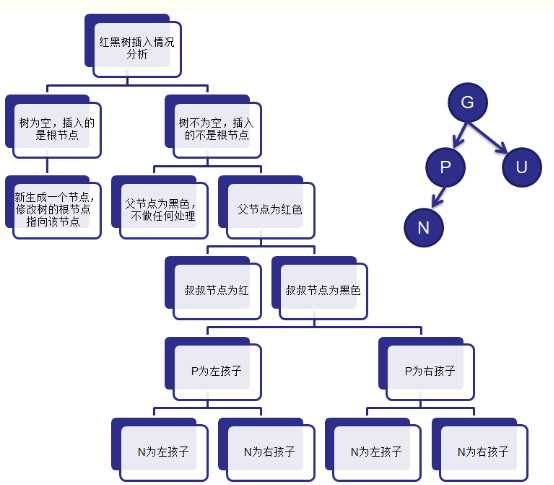
红父
如果新节点的父结点为红色,这时就需要进行一系列操作以保证整棵树红黑性质。如下图所示,由于父结点为红色,此时可以判定,祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作,而每次进行不平衡判断的起始点(我们可将其视为新点)都不一样。所以我们在此使用一个蓝色箭头指向这个起始点,并称之为判定点。
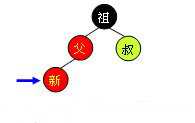
l 红叔
当叔父结点为红色时,如下图所示,无需进行旋转操作,只要将父和叔结点变为黑色,将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色,从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上(迭代)进行平衡操作。
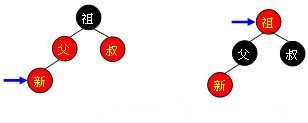
需要注意的是,无论“父节点”在“叔节点”的左边还是右边,无论“新节点”是“父节点”的左孩子还是右孩子,它们的操作都是完全一样的(其实这种情况包括4种,只需调整颜色,不需要旋转树形)。
l 黑叔
当叔父结点为黑色时,需要进行旋转,以下图示了所有的旋转可能:
Case 1:
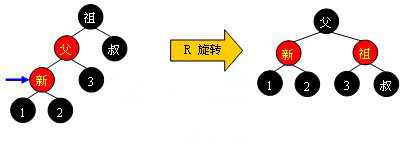
Case 2:
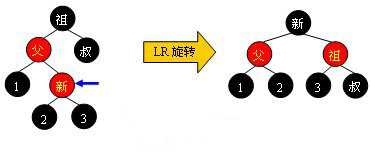
Case 3:
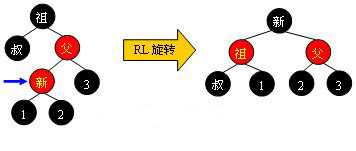
Case 4:
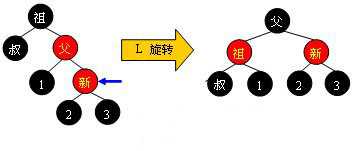
标签:蓝色 列操作 包括 决定 img back 分享 bubuko 平衡二叉查找树
原文地址:https://www.cnblogs.com/misscai/p/9595490.html