偏差（bias）和方差（variance）——KNN的K值、RF树的数量对bias和variance的影响

标签：相关   nbsp   结果   前言   曲线   bsp   方差   机器学习   泛化   

1.前言：为什么我们要关心模型的bias和variance？

　　大家平常在使用机器学习算法训练模型时，都会划分出测试集，用来测试模型的准确率，以此评估训练出模型的好坏。但是，仅在一份测试集上测试，存在偶然性，测试结果不一定准确。那怎样才能更加客观准确的评估模型呢，很简单，多用几份测试数据进行测试，取多次测试结果的均值，这样就可以平衡不同测试集带来的“偶然性”。就像跳水运动员比赛，都要经过第一跳、第二跳。。最后取总成绩来比高低，从而更加客观公正。

　　我们以跳水运动员来举例，假设运动员A，经过5次跳水（总分为10分），成绩分别为：9.0，8.8，9.1，8.6，8.9；运动员B，5次跳水成绩为：9.8，7.5，9.9，8.0，8.8。通过这两组数据，我们可以看出：

　　1. 运动员A的平均成绩在8.9左右，距离总分的偏差为1.1，每次的成绩相差不大，也就是方差较小；

　　2. 运动员B的平均成绩在8.8左右，距离总分的偏差为1.2，但是每次成绩相差很大，也就是方差较大；

　　我们可以得出以下结论：

　　1. A和B的平均成绩差不多，两个人水平可能不相上下；

　　2. A的发挥比较稳定，说明可能基本功扎实，综合素质较好，而B发挥不稳定，一会一鸣惊人，一会大跌眼镜，神经质一样。

　　如果让你选一个人作为代表去参加比赛，你会选谁？我想，一般教练都会选运动员A。当然，运动员B也是可塑之材，只要训练得当，可能比A更优秀。

　　其实，我们在测试集上评估的模型准确率，就如跳水运动员每次跳水的成绩。运动员A代表的模型，健壮性较好，泛化能力强；运动员B代表的模型，泛化能力差，有可能是过拟合。因此，我们不仅关心每一次评估结果的好坏，还要关心多次评估结果是否相差太大。我们不仅希望模型的准确率高（低bias），还希望模型能够表现的稳定（低variance）。所以，这就是为什么我们要关心模型的这两个指标。

2.偏差（bias）和方差（variance)

• 概念

　　通过上面的叙述，想必你对模型的bias和variance已有了一定的认识。接下来，我们用“行话“解释一下，什么是bias和variance。

　　所谓 bias，即模型的期望预测与真实预测的偏离程度。通俗讲，就是模型的预测误差。

　　所谓variance，即模型在不同训练样本上学习性能的变化，受数据扰动造成的影响。通俗讲，就是模型预测的稳定性，在不同数据集上的表现是否相差较大。

• 如何计算

　　如何计算一个模型的偏差和方差呢？举例来谈，假设我们利用训练样本训练出了一个模型M，接下来，我们准备5份不同的数据集作为测试数据，计算出5个测试误差率，分别为：e1，e2，e3，e4，e5。这5个值的均值就是bias，这5个值得方差就是various。bias = mean (e1，e2，e3，e4，e5)，variance = var (e1，e2，e3，e4，e5)。

• 应用

　　bias 和 variance 通常用来辅助判断模型的拟合状态，是欠拟合还是过拟合？下面还是通过经典的学习曲线图来加以说明吧。

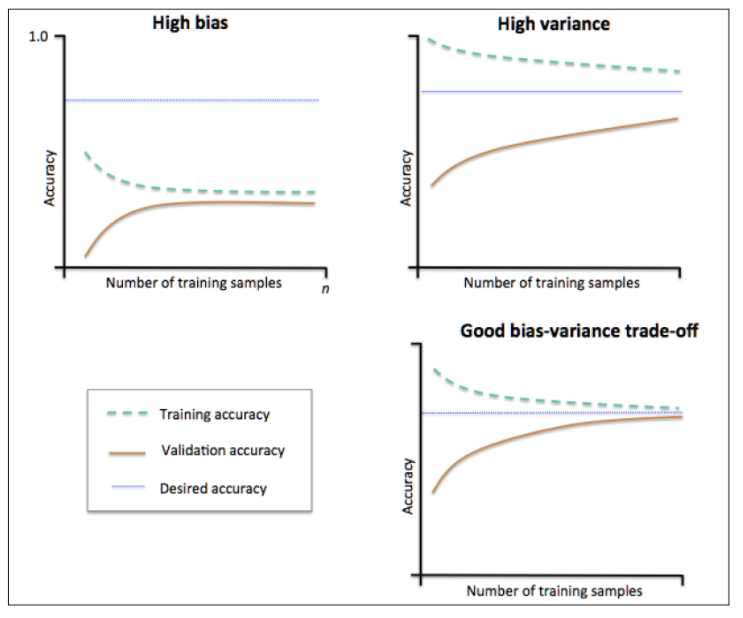
　　左上角的图，训练集和验证集的准确率都很低，为高bias，模型为欠拟合；

　　右上角的图，训练集和验证集的准确率较高，为低bias，但是训练集合验证集准确率相差较大（一般都是训练集准确率比验证集高），为高variance，模型过拟合；

　　右下角的图，训练集和验证集的准确率都较高、且两个值相差较小，为低bias，低variance，模型预测准确率高，泛化能力强，这就是我们的理想模型。

3. KNN的k值，RF树的数量对 bias 和 variance 的影响

• KNN

　　KNN中的k值，表示所取近邻样本的个数。首先我们看两个极端，当k值取1时，为最近邻算法， 新样本S的预测分类，取决于与它相似度最高的那一个样本所属的类别；当k取N时（N为样本数量），新样本的预测分类，取决于样本数据中哪一个类别的样本数量最多，已经跟样本记录间的相似度没有关系了。

　　当k取1时，根据最相似的一个样本判断分类，很有可能预测准确，为低bias，但是不同数据集中，与新样本S相似度最高的那个样本可能属于不同分类，那么预测结果则各不相同，为高variance。

　　当k取N时，完全根据样本数据的分布进行预测，不管新样本什么样，全部都会预测成样本数据中样本数量最多的那个类别。例如，有100个样本，60个属于A类，30个属于B累，10个属于C类，那么所有的新样本都会被预测为A类。此时为高bias，高variance。

　　当k值在1到N之间变化时，一定存在一个最优的k值，使得bias和variance最低，当大于或小于这个最优k值时，都会造成bias和variance变大。

• RF

　　首先，RF模型中各个树是“并联”关系，互不相关，每棵树都是“某个领域”的“分类专家”。当树的棵树较少时，模型的拟合效果不好，表现出高bias；逐渐增加树的数量，模型学习能力逐渐增强，bias和variance都会逐渐降低；当再继续增加树的数量时，这时对模型的bias和variance其实没什么影响，因为模型的bias已经趋于收敛，任你再怎么增加树的数量，只是增加了计算成本和训练时间，对模型精度的提高并没有多大影响。

　　以上是鄙人对bias和variance的一点拙见，如果有理解错误或表达错误的地方，希望不吝赐教，欢迎指正，谢谢！

偏差（bias）和方差（variance）——KNN的K值、RF树的数量对bias和variance的影响

标签：相关   nbsp   结果   前言   曲线   bsp   方差   机器学习   泛化   

原文地址：https://www.cnblogs.com/solong1989/p/9603818.html