标签：习题 公式 idt osb 适用于 定义 www 接下来 模拟
\(\fbox{例1}\)(2017\(\cdot\)陕西西安质检)
已知实数\(x，y\)满足\(x>y>0\)，且\(x+y=\cfrac{1}{2}\) ，则\(\cfrac{2}{x+3y}+\cfrac{1}{x-y}\)的最小值是_________.
分析：换元法，令\(x+3y=s>0\)，\(x-y=t>0\)，
求解上述以\(x，y\)为元的方程组，得到\(x=\cfrac{s+3t}{4}\)；\(y=\cfrac{s-t}{4}\)；
由\(x+y=\cfrac{1}{2}\)，将上述结果代入得到\(s+t=1\)，
故此时题目转化为"已知\(s+t=1\)，\(s，t>0\)，求\(\cfrac{2}{s}+\cfrac{1}{t}\)的最小值”问题。
接下来，利用乘常数除常数的思路就可以求解。
简单提示如下：\(\cfrac{2}{s}+\cfrac{1}{t}=(\cfrac{2}{s}+\cfrac{1}{t})(s+t)=3+\)\(\cfrac{2t}{s}+\cfrac{s}{t}\ge 3+2\sqrt{2}\)
(当且仅当\(\cfrac{2t}{s}=\cfrac{s}{t}\)及\(s+t=1\)时取到等号)
\(\fbox{例1-同类题}\)
已知实数\(a、b\)满足条件\(\left\{\begin{array}{l}{a+b-2\ge 0}\\{b-a-1\leq 0}\\{a\leq 1}\end{array}\right.\)，求\(\cfrac{a+2b}{2a+b}\)的取值范围。
【法1】转化为斜率型，
思路如下：由于所求值函数为分式形式的关于\(a、b\)的二次齐次式，
故可以转化为\(\cfrac{a+2b}{2a+b}=\cfrac{1+2\cdot \cfrac{b}{a}}{2+\cfrac{b}{a}}\)，
\(=2-\cfrac{3}{2+k}\)，其中\(k=\cfrac{b}{a}\)
这样先由可行域求得\(k=\cfrac{b}{a}\in [1，3]\)
然后用函数思想求得\(\cfrac{a+2b}{2a+b}\in [1，\cfrac{7}{5}]\)
【法2】换元法，令\(a+2b=n\)，\(2a+b=m\)，
联立解以\(a、b\)为元的方程组，得到
\(a=\cfrac{2m-n}{3}\)，\(b=\cfrac{2n-m}{3}\)，
代入原不等式组，可将原约束条件转化为关于\(m 、n\)的不等式组，
即已知\(m 、n\)满足条件\(\left\{\begin{array}{l}{m+n-6\ge 0}\\{n-m-1\leq 0}\\{2m-n-3\leq 0}\end{array}\right.\)，
求\(\cfrac{n}{m}\)的取值范围。
利用数形结合思想可得，\(\cfrac{a+2b}{2a+b}=\cfrac{n}{m}\in [1，\cfrac{7}{5}]\)。图像
\(\fbox{例2}\)
设点\(M(x，y)\)的坐标满足不等式组\(\begin{cases}x\ge 0\\y\leq 0\\x?y\leq 1\end{cases}\)，点\((m，n)\) 在点\(M(x，y)\)所在的平面区域内，若点\(N(m+n，m-n)\)所在的平面区域的面积为\(S\)，则\(S\)的值为______．
分析：由题可知，点\(M(x，y)\)的坐标满足条件\(\begin{cases}m\ge 0\\n\leq 0\\m?n\leq 1\end{cases}\)，
设\(m+n=s\)，\(m-n=t\)，则\(m=\cfrac{s+t}{2}\)，\(n=\cfrac{s-t}{2}\)，代入上述线性约束条件得到，
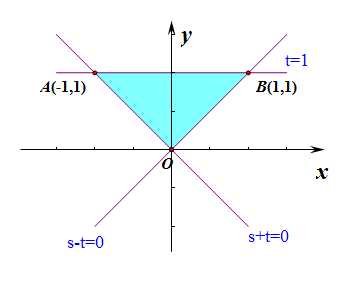
\(\begin{cases}s+t\ge 0\\s-t\leq 0\\t\leq 1\end{cases}\)，
做出不等式组对应的平面区域，如图中所示的阴影部分，
由题意可知，\(A(-1，1)\)，\(B(1，1)\)，
故\(S=\cfrac{1}{2}\times 2\times 1=1\)。
\(\fbox{知识点}\)三角函数和差化积等公式的推导，学生暂时不需要掌握这些知识，仅仅用此变换体会换元法。
在三角函数的学习中，我们知道这样的公式：
\(sin(A+B)=sinAcosB+cosAsinB\)；\(sin(A-B)=sinAcosB-cosAsinB\)；
则两式相加减，得到\(sin(A+B)+sin(A-B)=2sinAcosB①\)；\(sin(A+B)-sin(A-B)=2cosAsinB②\)；
令\(A+B=\alpha\)，\(A-B=\beta\)，
则解方程可知：\(A=\cfrac{\alpha+\beta}{2}\)，\(B=\cfrac{\alpha-\beta}{2}\)，
将这一结果代入①②式，就得到
\(sin\alpha+sin\beta=2sin\cfrac{\alpha+\beta}{2}cos\cfrac{\alpha-\beta}{2}③\)；
\(sin\alpha-sin\beta=2cos\cfrac{\alpha+\beta}{2}sin\cfrac{\alpha-\beta}{2}④\)；
如果我们对上述公式施行换元法的变换，
令\(\cfrac{\alpha+\beta}{2}=A\)，\(\cfrac{\alpha-\beta}{2}=B\)，
则\(A+B=\alpha\)，\(A-B=\beta\)，代入上述③④公式，得到
\(sin(A+B)+sin(A-B)=2sinAcosB\)；
\(sin(A+B)-sin(A-B)=2cosAsinB\)；
上述公式我们常常写作
\(sinAcosB=\cfrac{1}{2}[sin(A+B)+sin(A-B)]⑤\)；
\(cosAsinB=\cfrac{1}{2}[sin(A+B)-sin(A-B)]⑥\)；
\(\fbox{例4}\)求函数\(f(x)=sinx+cosx+sinxcosx\)的值域。
分析：令\(sinx+cosx=t\)，则由上例可知\(t\in[-\sqrt{2}，\sqrt{2}]\)，
则由\((sinx+cosx)^2=t^2\)得到\(sinxcosx=\cfrac{t^2-1}{2}\)，
故此时原函数经过换元就转化为\(f(x)=g(t)=t+\cfrac{t^2-1}{2}，t\in[-\sqrt{2}，\sqrt{2}]\)，和例1是同一类型的了。
\(\fbox{例11}\)(2017\(\cdot\)山西太原模拟)恒成立求参数范围
已知函数\(f(x)=(2a-1)x-\cfrac{1}{2}cos2x-a(sinx+cosx)\)在区间\([0，\cfrac{\pi}{2}]\)上单调递增，则实数\(a\)的取值范围是【】
A、\((-\infty，\cfrac{1}{3}]\) \(\hspace{2cm}\) B、\([\cfrac{1}{3}，1]\) \(\hspace{2cm}\) C、\([0，+\infty)\) \(\hspace{2cm}\) D、\([1，+\infty)\)
分析：由题目可知，\(f'(x)\ge 0\)在区间\([0，\cfrac{\pi}{2}]\)上恒成立，
\(f'(x)=2a-1-\cfrac{1}{2}\cdot (-sin2x)\cdot 2-a(cosx-sinx)\ge 0\)恒成立，
即\(2a-1+sin2x+a(sinx-cosx)\ge 0\)恒成立，
接下来的思路有：
思路一：分离参数，当分离为\(a\ge \cfrac{1-sin2x}{2+sinx-cosx}=g(x)\)时，你会发现，求函数\(g(x)_{max}\)很难，所以放弃；
思路二：转化划归，令\(sinx-cosx=t=\sqrt{2}sin(x-\cfrac{\pi}{4})\)，由于\(x\in [0，\cfrac{\pi}{2}]\)，故\(t\in [-1，1]\)
由\((sinx-cosx)^2=t^2\)，得到\(sin2x=1-t^2\)，
故不等式转化为\(at+1-t^2+2a-1\ge 0\)，
即\(t^2-at-2a\leq 0\)在\(t\in [-1，1]\)上恒成立，
令\(h(t)=t^2-at-2a，t\in [-1，1]\)，
则\(h(t)\leq 0\)等价于
\(\begin{cases}h(-1)=1+a-2a\leq 0\\h(1)=1-a-2a\leq \end{cases}\)
解得\(a\ge 1\)，故选D。
解后反思：
1、已知含参函数\(f(x)\)的单调性(比如单增)，求参数的取值范围，等价于\(f'(x)\ge 0\)，且还需要验证等号时不能让函数\(f(x)\)称为常函数，不过解答题一般不需要验证，是因为给定的函数比较复杂，当参数取到某个值是一般不会称为常函数。
2、转化为已知恒成立问题，求参数范围，一般首选分离参数的思路。
3、关于三角函数的这种转化必须熟练掌握。三角函数的转化
4、二次函数在某个区间上恒成立问题的模型必须熟练掌握。二次函数恒成立模型
\(\fbox{例2}\)求函数\(f(x)=4^x+3\cdot 2^x+1\)的值域。
分析：注意到函数的结果特点，做代数换元令\(2^x=t>0\)，则原函数就转化为\(f(x)=g(t)=t^2+3t+1，t\in(0，+\infty)\)上的值域，和上例就是同一个类型的题目。
\(\fbox{例3}\)求函数\(f(x)=x+\sqrt{1-x^2}\)的值域。
分析：求定义域得到\(x\in[-1，1]\)，故做三角换元令\(x=cos\theta,\theta\in[0，\pi]\)，则函数\(f(x)=x+\sqrt{1-x^2}=cos\theta+\sqrt{1-cos^2\theta}=cos\theta+|sin\theta|=sin\theta+cos\theta=\sqrt{2}sin(\theta+\cfrac{\pi}{4})\in[-\sqrt{2}，\sqrt{2}]\)，故函数的值域为\([-\sqrt{2}，\sqrt{2}]\)。
引申思考：
1、换元法特别需要注意的是旧元\(x\)和新元\(\theta\)的取值范围要一致，否则换元就会出错，那么本题中引入新元\(\theta\)后，其取值范围能不能是\([-\cfrac{\pi}{2}，\cfrac{\pi}{2}]\)？不能，否则\(cos\theta\in [0，1]\)，和\(x\in[-1，1]\)的取值范围不一致了。
2、那么取值范围能不能是\([0，2\pi]\)？此时虽然能保证\(cos\theta\in [-1，1]\)，但是下一步在开方去绝对值时就麻烦了，\(\sqrt{1-cos^2\theta}=|sin\theta|\)还需要分类讨论，这样反到复杂了，由此我们也就能更好的理解\(\theta\in[0，\pi]\)的用意，由此可知我们的三角换元是很讲究的，绝不是随心所欲的。
3、能不能这样换元令\(x=sin\theta\)？可以的，不过若这样换元，新元的范围就必须是\(\theta\in[-\cfrac{\pi}{2}，\cfrac{\pi}{2}]\)。
4、你会用这个方法求函数\(f(x)=x-\sqrt{2-x^2}\)的值域吗？
提示：定义域为\(x\in[-\sqrt{2}，\sqrt{2}]\)，故令\(x=\sqrt{2}cos\theta\)，则原函数转化为\(f(x)=x-\sqrt{2-x^2}=\sqrt{2}cos\theta-\sqrt{2}sin\theta=2cos(\theta+\cfrac{\pi}{4})\in [-2，2]\)。
5、你能将这一方法适用的类型做以总结提炼吗？
一般来说，适用于这样的类型：\(f(x)=ax+b\pm \sqrt{c+dx^2}\)型，其中\(a，b，c，d\in R，c\cdot d<0\)。
\(\fbox{例2}\)
已知\(\sqrt{1-x^2}>x+b\)在\([-1，\cfrac{1}{2})\)上恒成立，求实数\(b\)的取值范围。
法1：函数法，从数的角度入手，转化为\(b<\sqrt{1-x^2}-x\)，
令\(g(x)=\sqrt{1-x^2}-x\)，即关键是求\(g(x)\)在区间\([-1，\cfrac{1}{2})\)上的最小值。
令\(x=cos\theta，\theta\in (\cfrac{\pi}{3}，\pi]\)，
故\(g(x)=\sqrt{1-x^2}-cos\theta=sin\theta-cos\theta=\sqrt{2}sin(\theta-\cfrac{\pi}{4})\)，
因为\(\theta\in (\cfrac{\pi}{3}，\pi]\)，则有\(\cfrac{\sqrt{3}-1}{2}<\sqrt{2}sin(\theta-\cfrac{\pi}{4})\leq 1\)，
故\(b\leq \cfrac{\sqrt{3}-1}{2}\)。
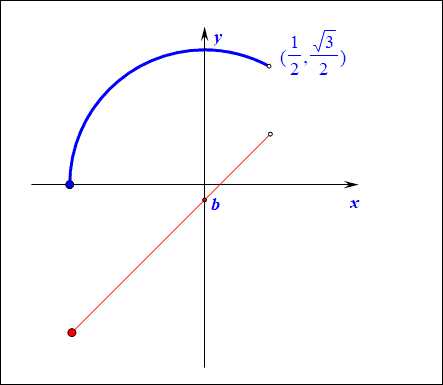
法2：数形结合，令\(f(x)=\sqrt{1-x^2}，x\in[-1，\cfrac{1}{2})\)，对应图中的蓝色的圆的一部分，
令\(h(x)=x+b，x\in[-1，\cfrac{1}{2})\)，对应图中的红色的线段，
由题目可知，要使得\(f(x)>h(x)，x\in[-1，\cfrac{1}{2})\)上恒成立，
则只需要\(h(x)\)的图像在\(f(x)\)的图像下方即可，
由动画可知，当线段经过点\((\cfrac{1}{2}，\cfrac{\sqrt{3}}{2})\)时，\(b=\cfrac{\sqrt{3}}{2}-\cfrac{1}{2}\)，
故\(b\leq \cfrac{\sqrt{3}-1}{2}\)。
标签：习题 公式 idt osb 适用于 定义 www 接下来 模拟
原文地址：https://www.cnblogs.com/wanghai0666/p/8571472.html
