20172302 《程序设计与数据结构》第一周学习总结

标签：内容   sum   图片   乘法   输入数据   void   数组   返回   出错   

2018下半年学习总结博客总目录：第一周

教材学习内容总结

第一章 概述

1.软件质量

软件工程(Software Engineering)是一门关于高质量软件开发的技术和理论的学科。

软件质量从以下八个方面进行考虑：

• 正确性 按照需求规范所规定的那样处理问题，在很大程度上满足其特定需求
  • 一、程序语法错误。
  • 二、程序对于几组输入数据能够得出满足需要的结果。
  • 三、程序对于精心选择的、典型、苛刻切带有刁难性的几组输入数据能够得出满足要求的结果。
  • 四、程序对于一切合法的输入数据都能得到满足要求的结果。
    
• 可靠性 应尽可能减少发生故障的频率，同时降低发生故障时所造成的损失
  
• 健壮性 在异常的状态能够对异常进行处理，而非发生异常就造成终止 。当输入的数据非法时，算法应当恰当的做出反应或进行相应处理，而不是产生莫名其妙的输出结果。并且，处理出错的方法不应是中断程序执行，而是应当返回一个表示错误或错误性质的值，以便在更高的抽象层次上进行处理。
  
• 可用性 软件的使用过程中的难易程度
  
• 可维护性 对软件部分代码进行修改的难易程度
  
• 可重用性 软件组件可重用于其他软件系统开发的难易程度
  
• 可移植性 软件组件在不同计算机环境下使用的难易程度
  
• 运行效率 在不浪费资源的情况下软件完成其目标的程度

2.数据结构

数据结构：把多个数据按照一定的存储方式,存储起来,称存储方式之为数据结构.
数据的存储方式有很多,数组,队列,链表,栈,哈希表等等. 不同的数据结构,性能是不一样的,比如有的插入比较快,查询比较快,但是删除比较慢. 有的删除比较快,插入比较快,但是查询比较慢. 根据实际操作,合理选择即可.

不同数据结构之间比较

第二章 算法分析

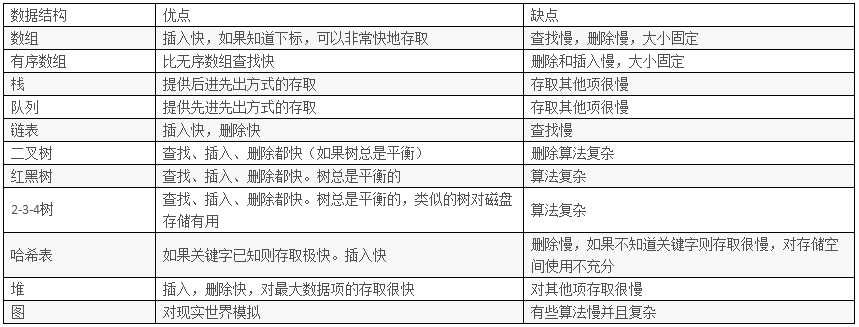
算法分析（analysis of algorithm）是计算机科学的基础，它是从效率角度对算法进行分类。
算法效率通常用CPU的使用时间来表示。

增长函数与大O记法

• 增长函数是表示问题（n）大小与我们希望最优化的值之间的关系，该函数表示了该算法的时间复杂度或空间复杂度。

• 渐进复杂度（asymptotic complexity）称为算法的阶次，随着问题大小的增加时增长函数的一般性质，这一性质取决于该表达式的主项，即n增加时表达式中增长最快的那一项。

• 大O记法：我们将算法具有阶次为n的时间复杂度，记为O（n）。
  

增长函数的比较

• 在给定时间内系统所能处理的最大问题，我们将处理器的速度提高10倍，这时再有系统所能处理的最大问题，见下表

• 各种增长函数之间的比较
  • n 较小时
    
  • n 较大时
    
• 结论：c(常量)<㏒?n < n < n㏒?n < n2< n3 < 2? < 3?< n!

时间复杂度分析

• 1.循环运行的复杂度分析
  首先确定循环体的阶n，然后乘以循环执行的次数

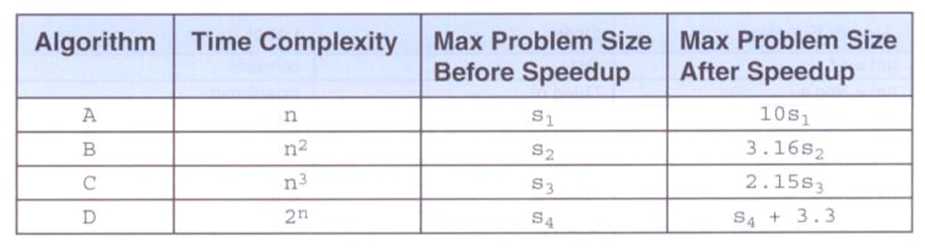
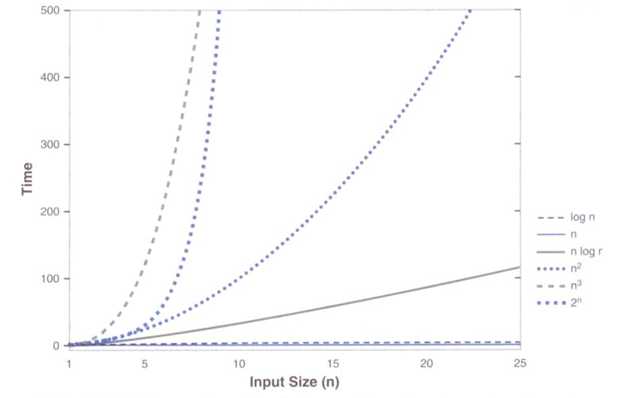
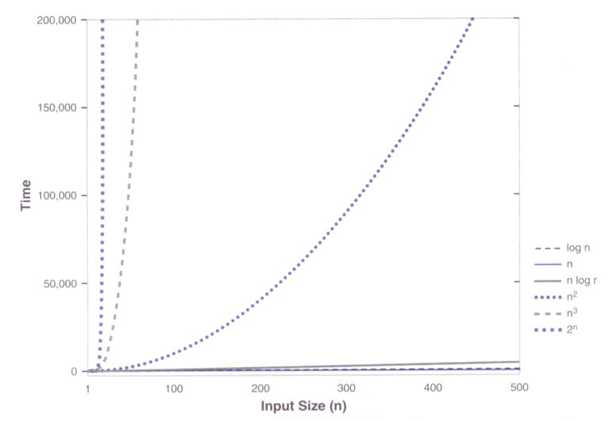
for (int count = 0; count < n; count++)
{
  // 复杂度为O(1)的步骤系列
}     

n * O(1) →O(n)

• 2.嵌套循环的复杂度分析
  循环出现嵌套时，循环的复杂度等于内层循环的复杂度乘以外层循环的复杂度

for (int count = 0; count < n; count++)
    for (int count2 = 0; count2 < n; count2++)
    {
        //复杂度为O(1)步骤系列
    }

内外层循环的复杂度均为O(n),整体的复杂度为O(n2)

• 3.方法调用的复杂度分析

循环体可能包含方法的调用，要确定循环体的阶，需要考虑调用方法的阶

for (int count=0 ;  count<n; count++)
{
Printsum(count);
}

以下是Printsum方法

Public void printsum（int count）
{
Int sum =0;
for(int i=0; i<count; i++)
sum += i;
System.out.println(sum);
}

于是整体的复杂度为O(n2)

时间复杂度的计算规则

• 1) 加法规则
  T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) )

• 2) 乘法规则
  T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))

• 3) 一个特例（问题规模为常量的时间复杂度）
  在大O表示法里面有一个特例，如果T1(n) ＝ O(c)， c是一个与n无关的任意常数，T2(n) = O ( f(n) ) 则有T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )。也就是说，在大O表示法中，任何非0正常数都属于同一数量级，记为O(1)。

课后练习题解答

其他（感悟、思考等）

感悟

参考资料

• Java中常见数据结构之间的区别
• Java数据结构与算法
• 时间复杂度的计算

20172302 《程序设计与数据结构》第一周学习总结

标签：内容   sum   图片   乘法   输入数据   void   数组   返回   出错   

原文地址：https://www.cnblogs.com/hzy0628/p/9606767.html