标签:教材 book 程序 总结 问题 ref 不同 查询 acm
void fun (int n){
int i=0;
while(i*i*i<=n)
i++;
}
for(int count = 0; count < n; count++)
{
//复杂度为O(1)的步骤系列
}
//复杂度为O(1×n)即O(n)for(int count = 0; count < n; count++)
{
for(int count2 = 0; count2 < n; count2++)
{
//复杂度为O(1)的步骤系列
}
}
//复杂度为O(1×n×n)即O(n^2)for(int count = 0; count < n; count++)
{
printsum(count);
}该代码段的复杂度要根据printsum方法的复杂度来确定,假如printsum方法为
public void printsum(int count)
{
int sum = 0;
for (int I = 1; I < count; I++)
sum += I;
System.out.println(sum);
}那么上面的代码段的复杂度就为O(n^2)。而假如printsum方法为
public void printsum(int count)
{
int sum = 0;
sum = count * (count + 1)/2;
System.out,println(sum);
}那么代码段的复杂度为O(n)。
问题1解决方案:书上的第九页有这么一段话
可靠性关注的是软件系统发生故障的频率以及在什么环境下发生故障,而健壮性关注的是软件系统出现故障时会发生什么。
我的理解是可靠性关注的是故障发生之前的相关内容,而健壮性关注的是故障发生之后的相关内容。
for(int count = 0 ; count < n ; count++)
for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
{
System.out.println(count,count2);
}
}for(int count = 0 ; count < n ; count++)//循环次数为n,复杂度为O(n^2)
for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)//循环次数为n/2,复杂度为O(n)
{
System.out.println(count,count2);//复杂度为O(1)
}
}为了确保正确性,我写了一个程序来实际测试了一下,发现的确内层的循环次数为n/2,外层的循环次数为n,证明增长函数和阶次是对的。
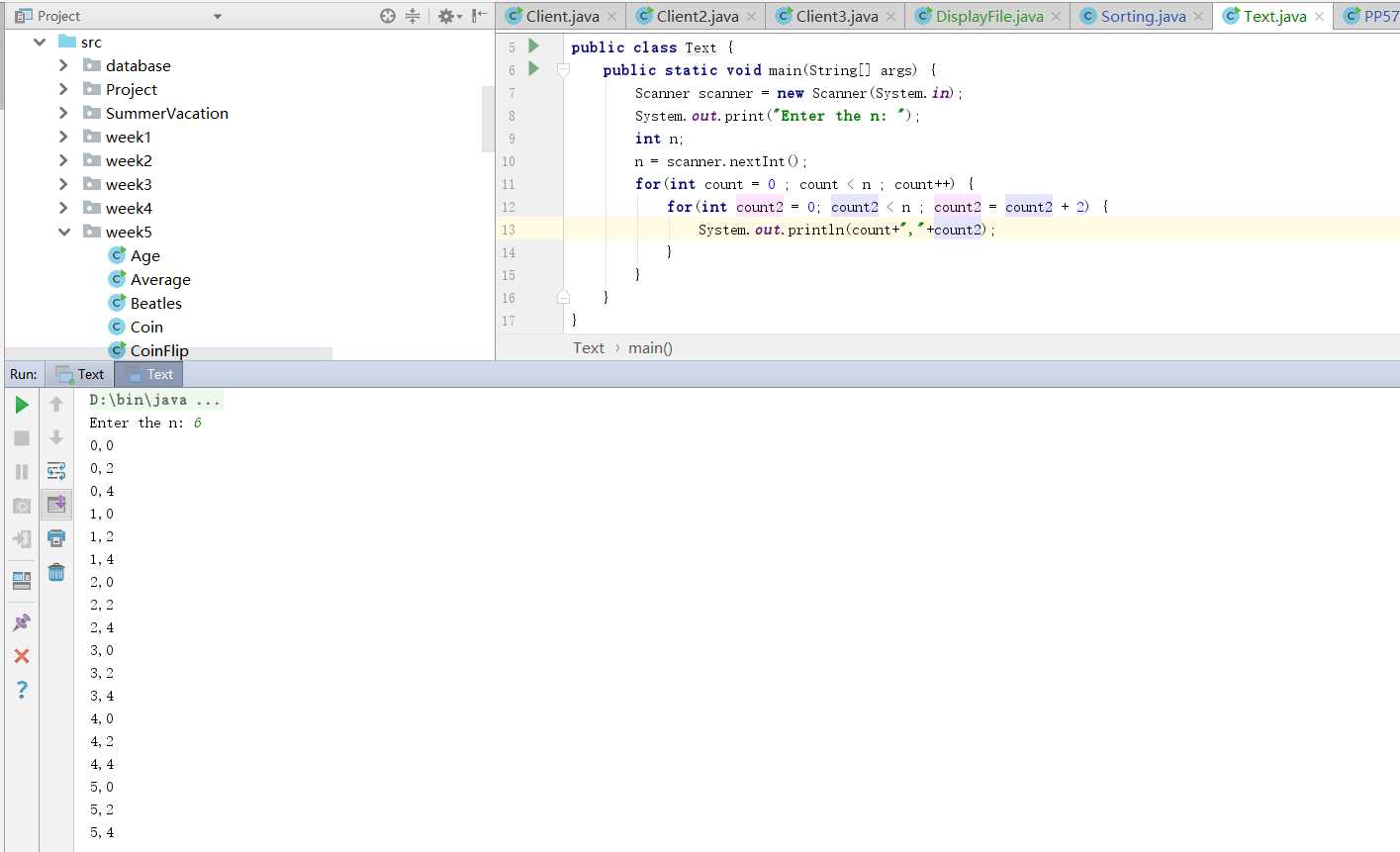
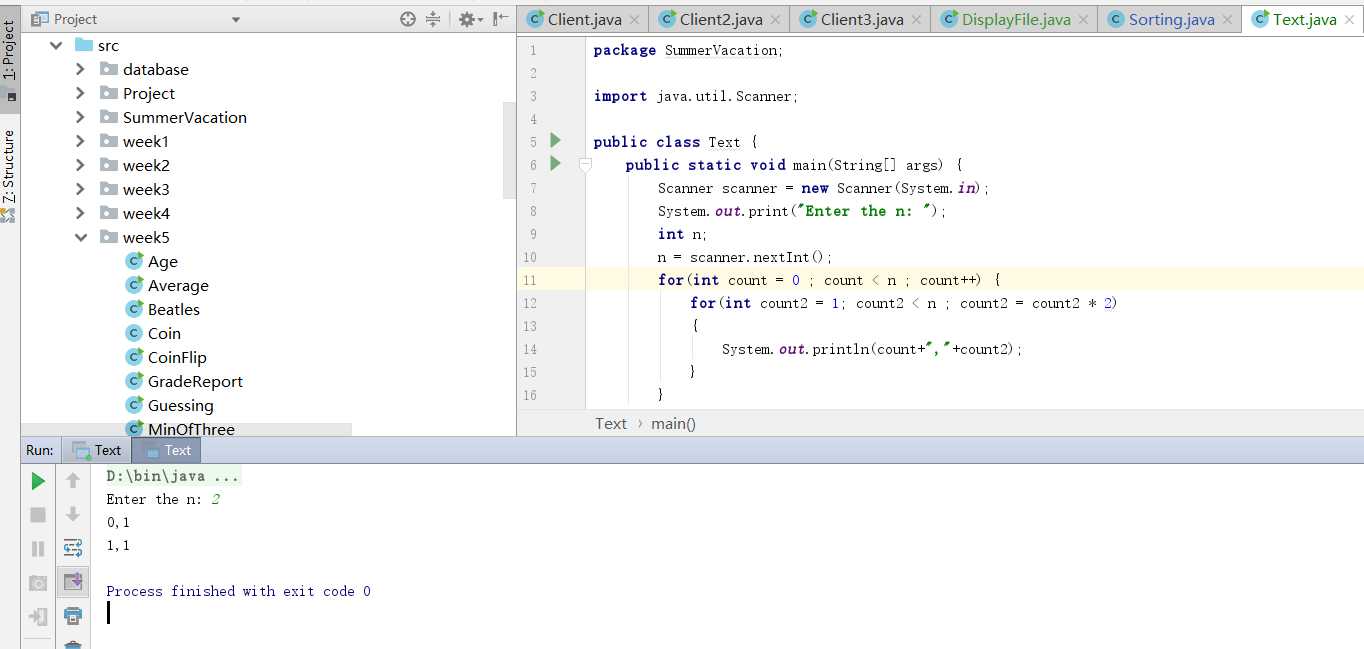
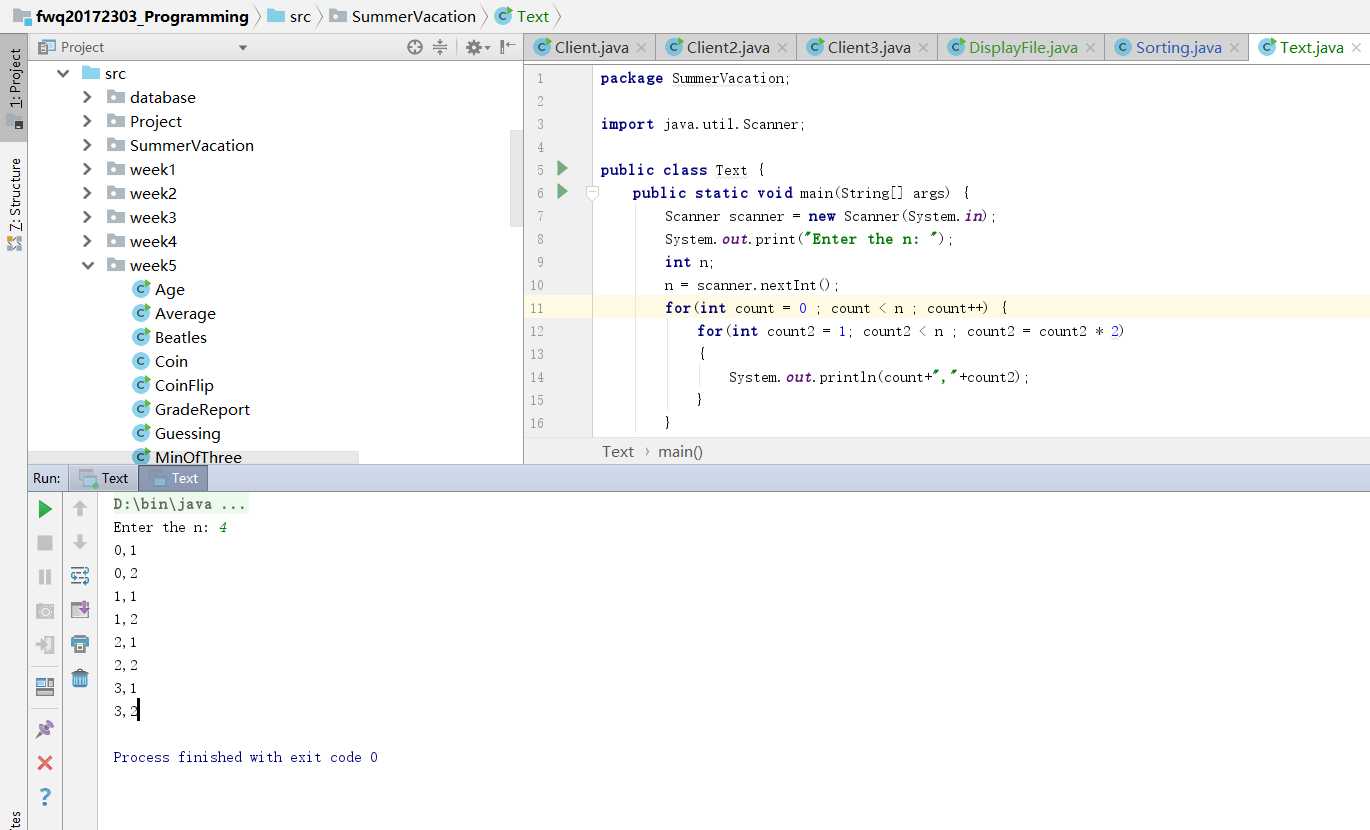
for(int count = 0 ; count < n ; count++)
for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
{
System.out.println(count,count2);
}
}for(int count = 0 ; count < n ; count++)//循环次数为n,复杂度为O(n×log2n)
for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)//循环次数为log2n,复杂度为O(log2n)
{
System.out.println(count,count2);//复杂度为O(1)
}
}再拿程序来测试一下:
新的一个学期又开始了,很惭愧上个学期期末靠着背单词和写博客拿了一个不错的分数。本学期的学习目标是希望自己的动手能力能够有所加强,不会的东西要多去试一试,不要只局限于知识,一定要学会应用。

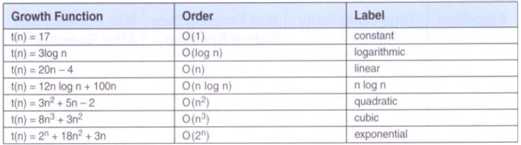
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 10/10 | 1/1 | 10/10 |
计划学习时间:5小时
实际学习时间:10小时
改进情况:本来感觉这周东西不多,老师还在课上都讲过了,没想到还是废了不少时间。本来尝试使用markdown语法去编辑公式,结果发现用不了,好像博客里给的方法只能在CSDN里面用o(╥﹏╥)o
20172303 2018-2019-1 《程序设计与数据结构》第一周学习总结
标签:教材 book 程序 总结 问题 ref 不同 查询 acm
原文地址:https://www.cnblogs.com/PFrame/p/9613948.html