标签:一个 答案 bin 两种 dia ges i+1 最大流 strong
In this problem you will have to deal with a very special network.
The network consists of two parts: part $ A $ and part $ B $ .
Each part consists of n vertices; $ i $ -th vertex of part $ A $ is denoted as $ A_i $ , and $ i $ -th vertex of part $ B $ is denoted as $ B_i $ .
For each index $ i (1?≤?i?<?n) $ there is a directed edge from vertex $ A_i $ to vertex $ A_{i?+?1} $ ,
and from $ B_i $ to $ B_{i?+?1} $ , respectively.
Capacities of these edges are given in the input.
Also there might be several directed edges going from part $ A $ to part $ B $ (but never from $ B $ to $ A $ ).
You have to calculate the maximum flow value from $ A_1 $ to $ B_n $ in this network.
Capacities of edges connecting $ A_i $ to $ A_{i?+?1} $ might sometimes change,
and you also have to maintain the maximum flow value after these changes.
Apart from that, the network is fixed (there are no changes in part $ B $ ,
no changes of edges going from $ A $ to $ B $ , and no edge insertions or deletions).
Take a look at the example and the notes to understand the structure of the network better.
The first line contains three integer numbers $ n, m $ and $ q (2?≤?n,?m?≤?2·10^5, 0?≤?q?≤?2·10^5) $
— the number of vertices in each part, the number of edges going from $ A $ to $ B $ and the number of changes, respectively.
Then $ n?-?1 $ lines follow, $ i $ -th line contains two integers $ x_i $ and $ y_i $ denoting
that the edge from $ A_i $ to $ A_{i?+?1} $ has capacity $ x_i $ and the edge from $ B_i $ to $ B_{i?+?1} $ has capacity $ y_i (1?≤?x_i,?y_i?≤?10^9) $ .
Then $ m $ lines follow, describing the edges from $ A $ to $ B $ .
Each line contains three integers $ x, y $ and $ z $ denoting an edge from $ A_x $ to $ B_y $ with capacity $ z (1?≤?x,?y?≤?n, 1?≤?z?≤?10^9) $ .
There might be multiple edges from $ A_x $ to $ B_y $ .
And then $ q $ lines follow, describing a sequence of changes to the network.
$ i $ -th line contains two integers $ v_i $ and $ w_i $ , denoting that the capacity of the edge from $ A_{v_i} $ to $ A_{v_i?+?1} $ is set to $ w_i (1?≤?vi?<?n, 1?≤?wi?≤?10^9) $ .
Firstly, print the maximum flow value in the original network.
Then print $ q $ integers, $ i $ -th of them must be equal to the maximum flow value after $ i $ -th change.
4 3 2
1 2
3 4
5 6
2 2 7
1 4 8
4 3 9
1 100
2 100 9
14
14
This is the original network in the example:
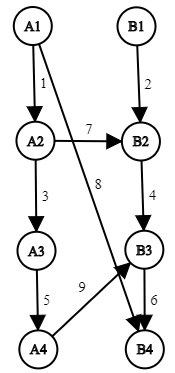
一张图分为两部分,左右都有 $ n $ 个节点,
$ A_i \rightarrow A_{i+1} $ 连边, $ B_i \rightarrow B_{i+1} $ 连边,容量给出
有 $ m $ 对 $ A_i \rightarrow B_j $ 有边,容量给出
两种操作
1.修改某条 $ A_i \rightarrow A_{i+1} $ 的边的容量
2.询问从 $ A_1 $ 到 $ B_n $ 的最大流
$ 2 \le n,m \le 2 \times 10^5 $ 流量 $ \le 10^9 $
感谢@yybyyb 提供的翻译
因为最大流的流量等于最小割的容量,所以最大流不好做的时候考虑最小割。
一些显而易见的结论:
假如在 $ A $ 中,割掉 $ A_x $ 和 $ A_{x+1} $ 之间的有向边,
那么割掉 $ A_y (y>x) $ 与 $ A_{y+1} $ 之间的有向边是没有意义的。
假如在 $ B $ 中,割掉 $ B_X $ 和 $ B_{x+1} $ 之间的有向边,
那么割掉 $ B_y (y>x) $ 与 $ B_{y+1} $ 之间的有向边是没有意义的。
因此,在 $ A, B $ 中至多有一条边属于割集。
假设在 $ A $ 中被割掉的边是 $ (A_x, A_{x+1}) $ ,在 $ B $ 中被割掉的边是 $ (B_y, B_{y+1}) $ ,
那么任意 $ (A_u, B_v) (u \ge x $ 且 $ v> y) $ 都是属于这个割集的。
因此,割的大小可以看作三部分:在 $ A $ 中的割集大小,在 $ B $ 中的割集大小,在 $ A, B $ 间的割集大小。
由于后两部分不会改变(只改 $ A $ 的边),考虑计算出它们。
考虑在 $ A $ 中从小到大枚举 $ A_x $ ,表示割掉 $ A_x $ 和 $ A_{x+1} $ 之间的边, $ x=n $ 表示不存在这条边。
那么下面要做的事情是在 $ B $ 中找到一个最优决策点 $ y $ ,使得后两部分的和最小。
对于每加入一条 $ A, B $ 间的边,对答案造成的影响是连续的一段,从 $ 1 $ 开始。
所以我们只需要写一个支持区间加,求 $ [1, n] $ 的最小值的线段树就好了。
合并两部分的答案。这个可以用一个可删堆或者线段树来维护。
时间复杂度 $ O((n+m+q)\quad log_n ) $
codeforces CF903G Yet Another Maxflow Problem 线段树
标签:一个 答案 bin 两种 dia ges i+1 最大流 strong
原文地址:https://www.cnblogs.com/PotremZ/p/9615148.html