Dimensionality Reduction

标签：ring   地方   很多   transform   如何   vector   方差   call   nbsp   

Dimensionality Reduction 

--Hands-on Machine Learning with Scikit-Learn and TensorFlow -Chapter 8

Introduction 

1. 降维 pros：有助于加快训练速度；有助于数据可视化。cons：可能会导致重要信息丢失。
2. Two main approaches to dimensionality:projection and manifold learning 
3. Three popular dimensionality reduction techniques:PCA,Kernel PCA, and LLE

Two main approaches for Dimensionalty Reduction

1. Projection 在实际问题当中，训练数据通常是非均匀的分布在整个维度里面。有很多特征是连续的，但是有一些特征非常相似。结果这些训练数据在低纬度空间中挨得非常近。
2. Manifold Learning （流形学习）

PCA(Principal Component Analysis) 

1. pca是迄今为止最流行的降维算法。首先定义一个超平面，然后将数据投影到上面去。
2. pca降维应当注意点地方：
2.1 preserving the variance 

2.2 the axis minimizes the mean squared distance between the original dataset and projection onto the axis

       3.　Principal Components:PCA identifies the axis that accounts for the largest amount of variance in the training set.

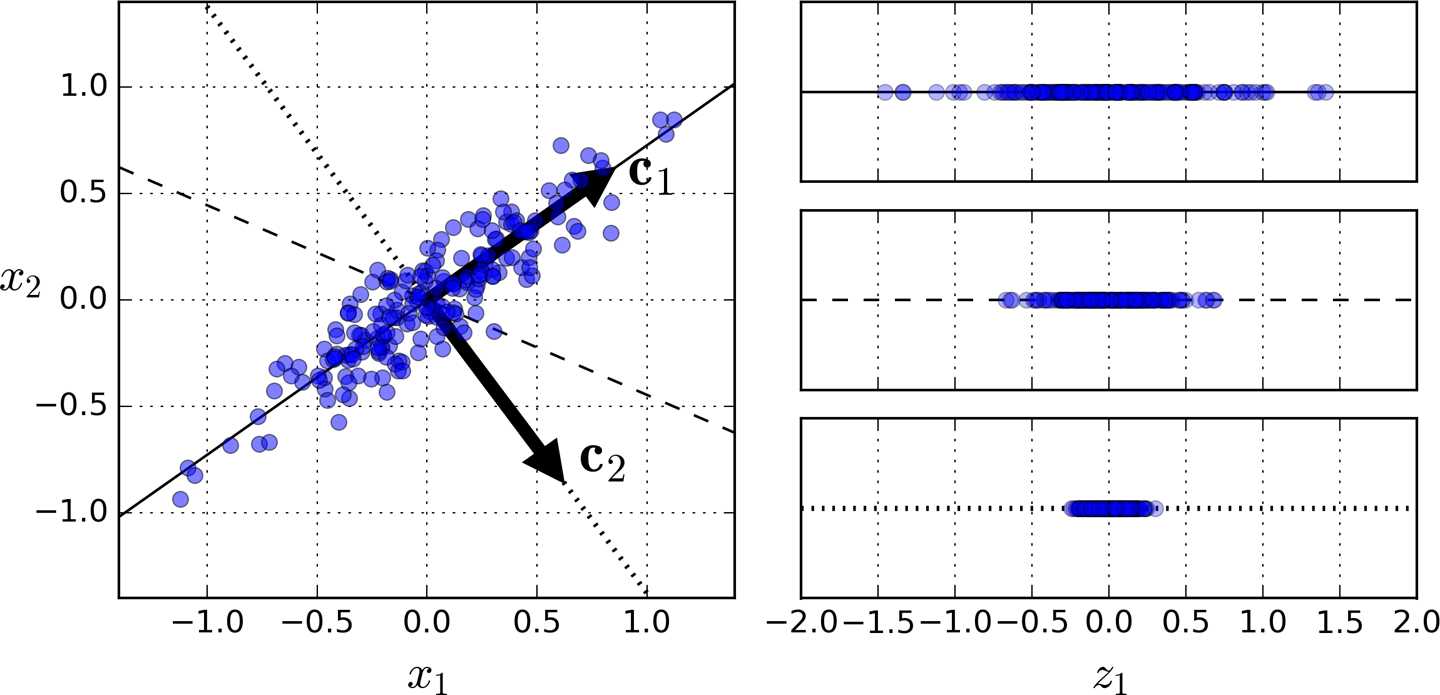
the unit vector that defines the i(th) axis is called i(th) principal component.

如何找到训练数据的主成分？Singular Value Decomposition(SVD)

PAC默认数据集是以愿数据为中心的。Sklearn 的pca 包已经将数据集中化处理了。而用其他方法构造pca时候，不要忘记首先集中化处理数据。（centering the data）

在降维的时候，一定要尽可能的保证更大的方差。

from sklearn.decomposition import PCA

pca=PCA(n_components=2)
X2D=pcd.fit_transform(X)
pca.explained_variance_ratio_

选择合适的维数

Dimensionality Reduction

标签：ring   地方   很多   transform   如何   vector   方差   call   nbsp   

原文地址：https://www.cnblogs.com/makino/p/9626871.html