luogu P3345 [ZJOI2015]幻想乡战略游戏（点分树）

时间：2018-09-11 22:00:19 阅读：217 评论：0 收藏：0 [点我收藏+]

标签：i++ 转移信息 cond 解决 printf 图片 while ack

题意自己看。。。

思路

没想到今（昨）天刷着刷着点分治的水题，就刷出来了一个点分树。。。

然后就疯狂地找题解，代码，最后终于把它给弄懂了。

点分树——动态点分治，对于此题来说，我们发现设u为当前的补给站位置，v是它的一个儿子。同时设dis(i,j)为树上i点到j点的距离。sum_i为以i为跟的子树中d（也就是军队数）的总量

我们把补给站从u转移到v，答案的变化为dis(u,v)*(sum_u-sum_v)-dis(u,v)*sum_v=dis(u,v)*(sum_u-2*sum_v)

所以当2*sum_v>sum_u把补给站转移v会使答案变优，一直这样操作下去，直到不管如何转移都无法使答案变优，当前点就是答案。

我们对于每一次修改都维护一下sum然后默认根为补给站，然后像刚才一样转移补给站，就有了这个题的大体思路。

但这样肯定会爆炸啊（每次只会转移一步，复杂度和深度有关）

所以我们就可以用到点分树了。

我们利用点分治的方法（找重心作为根节点，然后递归处理子树）重新构建一颗树，称为分治树。

举个例子，比如说样例

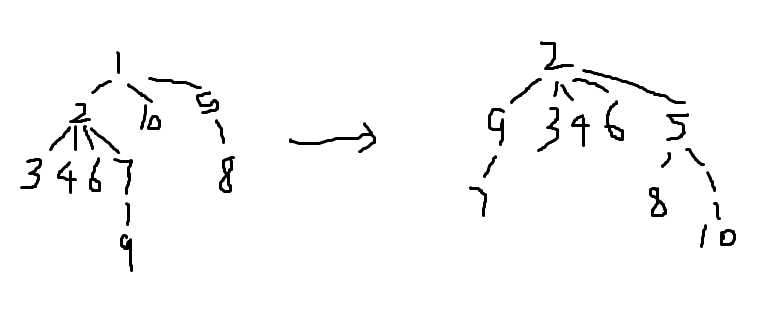技术分享图片（左为原树右为分治树）

这样我们就得到一颗深度为log的树。

这样我们转移就不会因为深度太大而GG了。

但是，这样一来的话因为树的结构不一样了，补给站的转移就会很难。因为一个点的儿子在原树中不一定和它直接相连（之后我们的补给站的转移都是在分治树上进行的）

但还是有办法解决的。我们记录这这些东西。dis(i,j)为i,j在原树的距离。cnt[i]为分治树中以i为根的子树中有多少个d，sumd_i为分治树中以i为根的子树中所有的点j的dis(i,j)*dj之和

最后一个答案数组sum_i，这个数组比较玄学，建议结合代码理解，当i为当前选定补给站时sun_i是所有的d_x*dis（x,i）

这个东西很好维护，我们预处理出每一个点在分治树中的每一个祖先，修改时，一个一个跳祖先就行了。

我们现在讨论从u转移到它分治树中的一个子节点v，v是原来这颗子树中的重心但在原树中并不一定和u之间相连，我们设原树中直接和u相连的点是w

只要把v所在子树之外的所有信息扔到w中然后递归就可以了。那怎么维护w的信息呢？

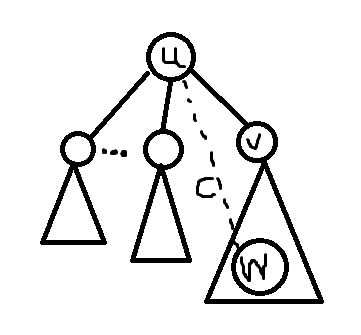
技术分享图片

我们记录在v处记录下w和w与u这条边的权值，然后我们在cnt_w处加上cnt[u]-cnt[v],然后在sum_w处加上sum[u]-sumd[v]+(cnt[u]-cnt[v])*c;

然后我们在维护的时候在w分治树的祖先的sum都加上sum_w,最后答案就取sum[当前点]就行了。

  1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdio>
  4 #include<vector>
  5 #include<cmath>
  6 #include<algorithm>
  7 using namespace std;
  8 #define ll long long
  9 typedef pair<ll,ll>p1;
 10 typedef pair<ll,p1>p2;
 11 const long long N=100100;
 12 vector<p1> pre[N];//存分治树祖先的编号，和原树中到祖先的距离 
 13 vector<p2> ch[N];//存与分治树的儿子，同一子树中的原树中的儿子，和连接原树中的儿子的边权 
 14 vector<p2> record;//回溯用 
 15 vector<ll> sumdist[N];//存分治树中的儿子的sum 
 16 long long tot,head[N];
 17 long long size[N],g[N],vis[N],all,realroot,root,n,m;
 18 long long sum[N],cnt[N];
 19 struct edge{
 20     long long to,nxt,w;
 21 }e[N<<1];
 22 void add(long long u,long long v,long long w){
 23     tot++;
 24     e[tot].nxt=head[u];
 25     e[tot].to=v;
 26     e[tot].w=w;
 27     head[u]=tot;
 28 }
 29 void get_root(long long u,long long fa){
 30     size[u]=1;
 31     g[u]=0;
 32     for(long long i=head[u];i;i=e[i].nxt){
 33         long long v=e[i].to;
 34         if(vis[v]==1||v==fa)continue;
 35         get_root(v,u);
 36         size[u]+=size[v];
 37         g[u]=max(g[u],size[v]);
 38     }
 39     g[u]=max(g[u],all-size[u]);
 40     if(g[u]<g[root])root=u;
 41 }
 42 void get_dis(long long u,long long fa,long long top,long long w){
 43     pre[u].push_back(p1(top,w));
 44     size[u]=1;
 45     for(long long i=head[u];i;i=e[i].nxt){
 46         long long v=e[i].to;
 47         if(vis[v]==1||v==fa)continue;
 48         get_dis(v,u,top,w+e[i].w);
 49         size[u]+=size[v];
 50     }
 51 }
 52 void work(long long u){
 53     vis[u]=1;
 54     pre[u].push_back(p1(u,0));
 55     for(long long i=head[u];i;i=e[i].nxt){
 56         long long v=e[i].to;
 57         if(vis[v]==1)continue;
 58         get_dis(v,0,u,e[i].w);
 59         root=0;all=size[v];
 60         get_root(v,0);
 61         ch[u].push_back(p2(root,p1(v,e[i].w)));
 62         work(root);
 63     }
 64 }
 65 void update(long long x,ll c,ll cc){
 66     for(long long i=0;i<pre[x].size();++i){
 67         long long u=pre[x][i].first;
 68         cnt[u]+=c;
 69         sum[u]+=cc+c*pre[x][i].second;
 70         if(i!=pre[x].size()-1){
 71             for(long long j=0;j<ch[u].size();j++)
 72                 if(ch[u][j].first==pre[x][i+1].first)sumdist[u][j]+=cc+c*pre[x][i].second;
 73         }
 74     }
 75 }
 76 ll query(){
 77     long long x=realroot;
 78     long long mx;
 79     record.clear();
 80     while(x){
 81         mx=0;
 82         for(long long i=1;i<ch[x].size();i++){
 83             if(cnt[ch[x][i].first]>cnt[ch[x][mx].first])mx=i;
 84         }
 85         if(ch[x].size()==0||cnt[ch[x][mx].first]*2<=cnt[x]){
 86             ll ans=sum[x];
 87             for(long long i=0;i<record.size();i++){
 88                 update(record[i].first,record[i].second.first,record[i].second.second);
 89             }
 90             return ans;
 91         }
 92         long long v=ch[x][mx].first;
 93         record.push_back(p2(ch[x][mx].second.first,p1(-(cnt[x]-cnt[v]),-(sum[x]-sumdist[x][mx]+(cnt[x]-cnt[v])*ch[x][mx].second.second))));
 94         update(ch[x][mx].second.first,cnt[x]-cnt[v],sum[x]-sumdist[x][mx]+(cnt[x]-cnt[v])*ch[x][mx].second.second);
 95         x=v;
 96     }
 97 }
 98 int main(){
 99     scanf("%lld%lld",&n,&m);
100     for(long long i=1;i<=n-1;++i){
101         long long u,v,w;
102         scanf("%lld%lld%lld",&u,&v,&w);
103         add(u,v,w);
104         add(v,u,w);
105     }
106     g[0]=n+10;root=0;all=n;
107     get_root(1,0);realroot=root;
108     work(root);
109     for(long long i=1;i<=n;++i){
110         sumdist[i]=vector<ll>(ch[i].size(),0);
111     }
112     while(m--){
113         long long x,y;
114         scanf("%lld%lld",&x,&y);
115         update(x,y,0);
116         printf("%lld\n",query());
117     }
118     return 0;
119 }

luogu P3345 [ZJOI2015]幻想乡战略游戏（点分树）

标签：i++ 转移信息 cond 解决 printf 图片 while ack

原文地址：https://www.cnblogs.com/Xu-daxia/p/9630536.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行