标签:特性 之间 数据规模 tco += 分享图片 n+1 mat 搜索
几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第k小的数字吗?
给定高度m 、宽度n 的一张 m * n的乘法表,以及正整数k,你需要返回表中第k 小的数字。
例 1:
输入: m = 3, n = 3, k = 5 输出: 3 解释: 乘法表: 1 2 3 2 4 6 3 6 9 第5小的数字是 3 (1, 2, 2, 3, 3).
例 2:
输入: m = 2, n = 3, k = 6 输出: 6 解释: 乘法表: 1 2 3 2 4 6 第6小的数字是 6 (1, 2, 2, 3, 4, 6).
注意:
m 和 n 的范围在 [1, 30000] 之间。k 的范围在 [1, m * n] 之间。1.直观思路:首先生成乘法表,将所有数据放到一个集合中,对集合进行排序,但是这道题的数据规模比较大,这张乘法表过于巨大,无法使用暴力!
2.那我们怎么做?
由于乘法表中的每一行都是排过序的,我们很容易得知某一行有多少元素小于或大于特定值。 这道题数据规模巨大,绝对不可能采用存储并运算的方式,所以诸如堆排序也是不可能的。分析问题我们很明显是查找问题,且数据具有一定的特性,直接思路靠到二分查找上。
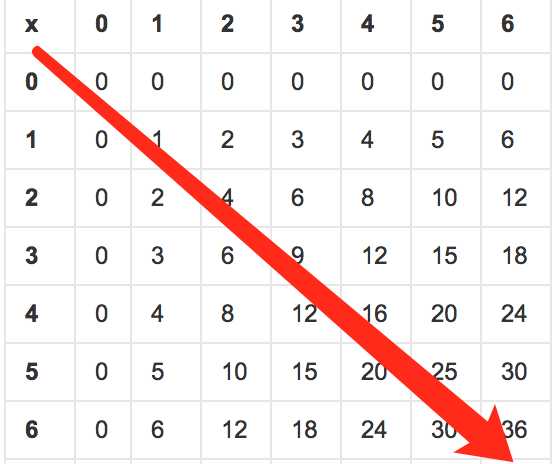
3.啥叫数据特性?具体规律是怎样的。
切记,我们利用这个数据特性是为了快速统计有多少个元素小于或等于特定值。
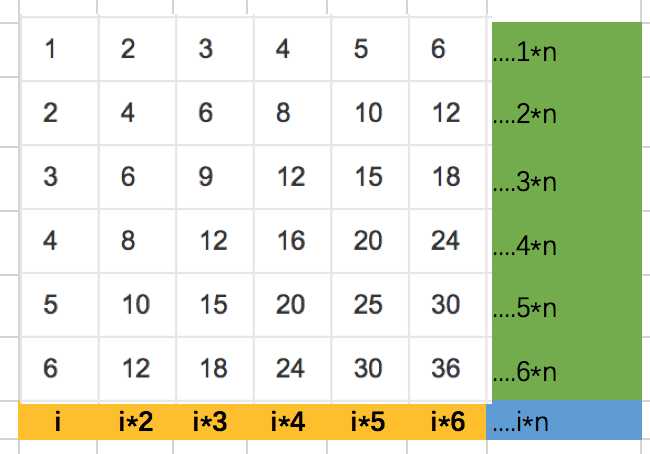
每一行有多少个小于特定值的元素呢,我们可以将特定值x除以i,然后其值就可以看做是个数(因为没有比例放大),如果这个数小于n的话,最多就是x/i,否则就是大于全员,那么这行n个元素全部小于x。然后我们用二分搜索的套路,不断缩小范围,直到找到小于它的元素是K个的。
class Solution {
public int findKthNumber(int m, int n, int k) {
int l =1;
int r = m*n+1;
while(l<r)
{
int x = l+(r-l)/2;
if(LEX(m,n,x)>=k)
r=x;
else
l=x+1;
}
return l;
}
private int LEX(int m,int n,int x)
{
int count = 0;
for(int i=1;i<=m;i++)
count+=Math.min(n,x/i);
return count;
}
}
标签:特性 之间 数据规模 tco += 分享图片 n+1 mat 搜索
原文地址:https://www.cnblogs.com/MrSaver/p/9631854.html