标签:tle 说明 常见 http bubuko 除了 item 分支 out
最近写了很多笔试题,发现关于二叉树的好多概念还是没有完全理清,总结一下;
这是百度百科给的几种二叉树的类型:
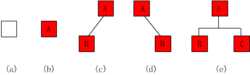
然后还有一点要说明的是二叉树不是树的特殊类型,他们相似也有很多不同点:
树具有的特点有:
(1)每个结点有零个或多个子结点
(2)没有父节点的结点称为根节点
(3)每一个非根结点有且只有一个父节点
(4)除了根结点外,每个子结点可以分为多个不相交的子树。
几个常见的术语:
“双亲”——子树根上面的节点;“孩子”——上面那个节点下子树的根;就跟我们的亲属关系类似还有“兄弟”、“祖先”、“后裔”等说法很好理解。
结点的度:结点拥有的子树的数目
叶子结点:度为0的结点
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
树的高度:树中结点的最大层次
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
二叉树一些性质,经常会有根据性质来的笔试题出现:
1:二叉树第i层上的结点数目最多为2i-1(i>=1)
2:深度为k的二叉树至多有2k-1个结点(k>=1)
3:包含n个结点的二叉树的高度至少为(log2n)+1
4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
5:如果一棵完全二叉树的结点总数为n,那么叶子结点等于n/2(当n为偶数时)或者(n+1)/2(当n为奇数时)
标签:tle 说明 常见 http bubuko 除了 item 分支 out
原文地址:https://www.cnblogs.com/luza/p/9634230.html