标签:递归树 额外 级别 不为 inf 一个 技术 bubuko src
递归中,一个规模为n的问题分成a个规模为n/b的问题,额外计算复杂度为c*n^d,那么
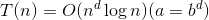
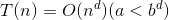
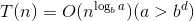
我们画出递归树,则递归树共有logb(n)+1层。对于第j层,有a^j个子问题,每个子问题规模为n/b^j。
则第j层所用时间为
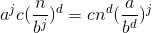
接下来求所有层的和
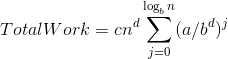
根据a与b^d的大小讨论,易得主定理中结论
若不为平均分,则设最大的一部分为p*n(0 < p < 1),则树的深度为
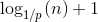
又由于
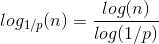
所以深度依旧是log(n)级别
由于快排分割随机,所以我们考虑平均复杂度。
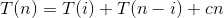
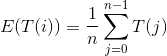
所以有
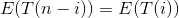
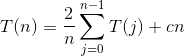
两边同乘以n
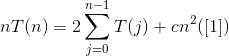
又有
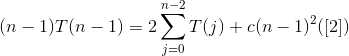
[1] - [2] 得
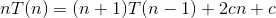
两边同除n*(n+1)得
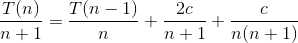
累加求和,得
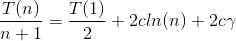
//γ为欧拉常数
所以
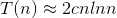
标签:递归树 额外 级别 不为 inf 一个 技术 bubuko src
原文地址:https://www.cnblogs.com/chy-2003/p/9639494.html