标签:++ priority for string add struct 注意 span info
题意:有n个地方,m条带权值的路,你有k次机会将一条路的权值变为0,求1到n的最短距离。
分析:这是一题分层dijkstra的模板题,因为k的大小不是很大,最坏的情况也就是10,而我们一般的最短路问题只是建一个平面的图。
而分层dijkstra是一个空间的。怎么操作呢?
举个简单的栗子
当数据如下是
n m k
3 2 1
1 2 5(路的起点1,终点2,权值5)
2 3 6
没有k的情况就是这样的
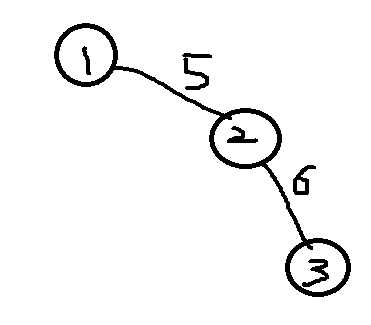
如果有k的情况,即1到2权值可能为0,2到3也可能为0,我们可以加一个平面表示他们的关系
将4,5,6(地方)表示1,2,3的关系图形如下:(图很丑,将就着看。。。)
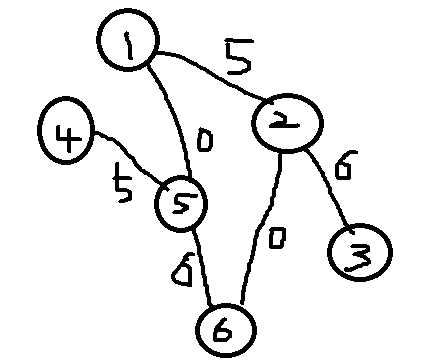
为什么这样表示呢? 因为我们可能理解1到2可能变成0,所以1到5的距离为0,2到3可能变为0即2到6距离为0.
答案就是1到3的最短路与1到6的最短路最小值。
我们可以通过这样一个简单的例子来理解:
1.k的大小关系到分的层数(k+1层)。
2.只有层与层之间的路才为0,这样使用的k值就不会超过给定的。
3.而答案可能没用到k,那答案就是1到n的最短路,如果用一次就是1到2*n的最短路,如果用k次就是1到(k+1)*n的最短路
所以答案就是min(d[n],d[n*2]....d[(k+1)*n]) (d[]表示1到其的距离)。
这个方法很巧妙地避免了使用k的问题。只要先建好图,直接用dijkstra.
这里还要注意几个问题:
1.图的存储方式,m的范围有点大,不能用邻接矩阵,这里用的是链式前向星,邻接表也可以。
2.数组的大小,因为图最坏是11层(最坏11*m),层与层之间也有路(最坏10*m),所以最少要开21*m的数组
3.这里用了优先队列,防止时间超时。(不知道不用会不会超时,没试过)。
代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const ll maxn=3e6+10; struct node{ ll from,to; ll next; ll w;//权值 }edge[2*maxn];//前向星 struct point{ ll y,val; }t,p; ll head[maxn],visit[maxn],d[maxn]; ll ans,cnt,k,n,m; bool operator < (point a,point b)//优先路径短的 { if(a.val==b.val) return a.y<b.y; return a.val>b.val; } priority_queue<point> q; void init() { memset(head,-1,sizeof(head)); memset(visit,0,sizeof(visit)); memset(d,0x3f,sizeof(d)); cnt=0; } void add(ll u,ll v,ll w)//前向星加边 { edge[cnt].from=u; edge[cnt].to=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++; } void dijkstra(int u,int v)//dijkstra { d[u]=0; t.y=u,t.val=0; q.push(t); while(!q.empty()) { p=q.top(); q.pop(); if(visit[p.y]) continue; visit[p.y]=1; for(int i=head[p.y];i!=-1;i=edge[i].next) { int e=edge[i].to; //cout<<e<<endl; if(d[e]>d[p.y]+edge[i].w) { d[e]=d[p.y]+edge[i].w; t.y=e,t.val=d[e]; q.push(t); } } } ans=inf; for(int i=0;i<=k;i++)//取d[n],d[n*2]...d[(k+1)*n]最小 { if(ans>d[v+i*n]) ans=d[v+i*n]; } cout<<ans<<endl; } int main() { int t; scanf("%d",&t); while(t--) { init(); scanf("%lld%lld%lld",&n,&m,&k); if(k>=m)//k大于边数,无疑答案是0 { cout<<0<<endl; continue; } for(int i=1;i<=m;i++) { ll u,v,w; scanf("%lld%lld%lld",&u,&v,&w); for(int j=0;j<=k;j++) { add(u+j*n,v+j*n,w);//每一层地方的关系,建图 if(j!=k) add(u+j*n,v+(j+1)*n,0);//层与层之间的关系,建图 } } dijkstra(1,n); } return 0; }
ACM-ICPC 2018 南京赛区网络预赛 L. Magical Girl Haze(分层dijkstra)
标签:++ priority for string add struct 注意 span info
原文地址:https://www.cnblogs.com/xiongtao/p/9642152.html