标签:tree splay 搜索 str 局限性 局限 lan 递归查询 printf
【引言】在上一篇博客中探讨了树状数组的原理以及用法,我们知道:树状数组是一种擅长多次单点修改和区间查询的数据结构。但是我们很容易抛出这样一个问题:如果是区间修改,区间查询呢?我们来看这样一个问题:
给定一个长度为N的数列,有如下两种操作:
(1) Q L R 查询区间L - R的元素总和;
(2)C L R X 把区间L - R的元素全部加X;
现有M次操作,对于每次Q操作都输出对应结果。 1 ≤ N,Q ≤ 100000.
【问题分析与解决】
首先我们思考树状数组怎么解决这个问题,由于树状数组只能单点修改难道对区间L - R每一个点都进行单点修改吗?这样太不划算。
聪明的人可能想到可以用差分数组解决这个问题令c[i] = a[i] - a[i-1] ,经过和式推导我们可以得出:
a[1]+a[2]+...+a[n]
= (c[1]) + (c[1]+c[2]) + ... + (c[1]+c[2]+...+c[n])
= n*c[1] + (n-1)*c[2] +... +c[n]
= n * (c[1]+c[2]+...+c[n]) - (0*c[1]+1*c[2]+...+(n-1)*c[n])
= 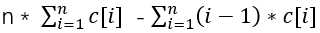
再维护一个d[i] = (i-1) * c[i]的d数组, 建立c d数组的树状数组,不久可以解决这个问题了吗?
有兴趣的读者可自行实现这个问题,此处不再赘述。
那么除了这种需要技巧的处理我们如何专门解决这一类区间修改区间查询的问题呢? 我们有一种比树状数组更强大的数据结构:线段树。
【线段树】
顾名思义,这棵树中包含线段,什么是这棵树的线段呢?其实就是这颗树的每一个结点代表的是一个区间,像线段一样,有左右端点。
来看这样一幅图:
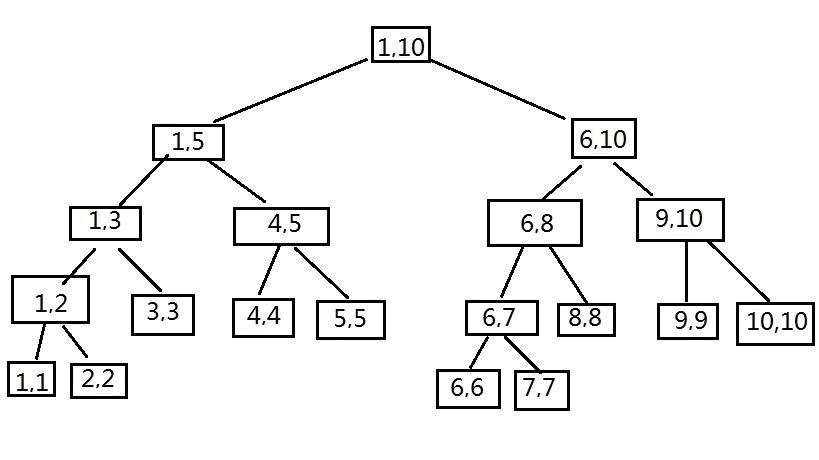
我们很容易看出它是将原来的区间1 - N,不断递归分成左右两半,直到分到区间长度为1为止(此时就是叶子节点了不用再分),每个节点都维护了该结点所代表的区间的区间元素和。回到引言中抛出的问题,比如说我要查询6 - 10的元素区间和,那么很好办,我从树的根节点1号结点出发,根节点代表的区间是1-10, 中点是5, 发现6 -8在我中点的右边,那我便要去我的右孩子结点取寻找,发现是6-10,然后到左孩子结点寻找,发现正好左孩子代表的区间是6-8,所以就返回该结点所维护的区间和。
由于是类似二叉树的搜索,时间复杂度是O(logN),效率是比较高的。
【问题提出】
有人可能会问:
(1)假如我查询的区间是3 - 6呢,图中也没有代表3 - 6的区间的结点啊?
答:把【3,6】拆分成【3,3】、【4,5】、【6,6】的三个子区间的和。
(2)那我要修改某一区间的元素呢?那么不仅仅是这一区间的元素和发生了变化,某些区间不也要跟着一起变吗?
答:这个问题和第一个问题差不多。在树状数组中,更新原数组某一元素时(假如下标为i),控制这个元素的树状数组的很多部分都要更新。哪些部分呢,如我在上篇博客中总结的,不断往上迭代i += lowbit(i),更新所有的c[i],直到i>n为止。那么在此处,我们要考虑被修改的区间是被哪些区间所控制。比如修改了【5,8】,那么5,6,7,8这些叶子结点的所有祖先结点全部都要更新。因为祖先结点控制了子孙结点。
(3)更新一个区间,那么这个区间的所有的叶子结点的所有祖先结点都要更新,效率太低了吧?!
答:问得好!我们其实可以发现这样几个事实:
A. 修改是为了查询服务的。你如果不查询,你给我改的指令我不改你也没办法,因为你不查啊,你不查我就懒得改。
B.我每次查只要查到最近的能满足需求的结点然后返回它的区间和就行了。比如说我查询3 - 6,那么我查询【3,3】、【4,5】、【6,6】这几个子区间就可以了,没必要在查到【4,5】时还往下查【4,4】、【5,5】。再比如我查【6,10】区间,第一步我从【1,10】出发然后进入右孩子结点发现找到了,恰好能满足我需要查询的区间,那我直接返回该结点的区间和就好了没必要再往下查。
从A、B两点出发,我们引入了一种标记,名字叫做lazy标记。
【Lazy标记】
(1)每一个结点都有一个lazy标记.
结点结构:
struct node{ int l,r;//区间端点 int len;//区间长度 ll sum;//区间和 ll lazy;//懒标记 }tree[maxn<<2];
为什么结构体数组要开maxn的4倍空间?
因为建树的时候其实建立的是一棵完全二叉树(虽然抽象出的模型不是完全二叉树),所有叶子结点其实还有左右孩子,只不过他们是空,但是结点标号还在。
(2)该结点的lazy标记不为初始值(一般初始值设置成0)代表,我的所有子孙结点都没有被更新。
(3)根据(2)以及之前问题的B特性,我们知道由于查询的就进原则,虽然我的子孙结点的区间和暂时没有更新,但是没有任何影响,因为我已经更新了,你查的时候只会查到我,不会查我的子孙。只要我是对的就可以了。
(4)根据(3)我们知道了针对查询操作的偷懒原理。但是纸包不住火,迟早有一天我的子孙结点是要被查的。所以我的懒标记需要下传,下传给我的左右孩子结点告诉他们要准备改啦。一旦我的标记下推,我的懒标记就可以清零代表我已经没有偷懒l了。(其实我还是偷懒了因为我只传递给了我的左右孩子,我的孙子曾孙子都没收到这个懒标记,但是我不管,需要的时候找我的左右孩子要吧)。
下传标记操作 pushDown函数:
void pushDown(int rt){ if(tree[rt].lazy){ //更新子节点的sum tree[rt<<1].sum += tree[rt].lazy * tree[rt<<1].len; tree[rt<<1|1].sum += tree[rt].lazy * tree[rt<<1|1].len; //下推标记 tree[rt<<1].lazy += tree[rt].lazy;//lazy标记是累加式的防止上一次更新还没做这一次更新要带着上次一起做 tree[rt<<1|1].lazy += tree[rt].lazy; //根节点懒标记清零 tree[rt].lazy = 0; } }
(5)相对于pushDown函数,还有一个pushUp函数,它是用来根据左右孩子的区间和更新根节点区间和的函数,向上保持正确。
void pushUp(int rt){ tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum; }
【核心操作】
(1)建树
void build(int rt, int l, int r){ tree[rt].l = l;//左端点赋值 tree[rt].r = r;//右端点赋值 tree[rt].lazy = 0;//懒标记初始值记为0 tree[rt].len = r - l + 1;//区间长度赋值 if(l == r){//到了叶子节点 //tree[rt].sum = 1;//初始化为1 tree[rt].sum = a[l] ;//原来的数组a[] return; } int mid = (l + r) >> 1; build(rt<<1 , l, mid);//递归建立左子树 build(rt<<1|1, mid+1, r);//递归建立右子树 pushUp(rt);//回溯更新所有区间和 }
(2)更新
void update(int rt, int l , int r, int val){ //如果待更新区间[l,r]恰好是当前结点的区间则直接更新当前结点 if(tree[rt].l == l && tree[rt].r == r){ tree[rt].sum += val * tree[rt].len; tree[rt].lazy += val; return ; } //告诉我的左右孩子要更新了,爸爸已经更新了 pushDown(rt); int mid = (tree[rt].l + tree[rt].r) >> 1; // 递归更新 ,给待更新区间 [l,r]分段更新直到满足上面的可以直接更新的条件 if(l > mid){ update(rt<<1|1, l , r, val); } else if(r <= mid){ update(rt<<1, l , r, val); } else{ update(rt<<1, l , mid, val); update(rt<<1|1, mid+1 , r, val); } //向上保持正确 pushUp(rt); }
(3)查询
ll query(int rt, int l , int r){ ll ans = 0; if(tree[rt].l ==l && tree[rt].r == r){ //如果待查区间[l,r]恰好是当前结点的区间则直接返回 return tree[rt].sum; } pushDown(rt);//下推懒标记告诉我的左右孩子要更新了 //递归查询 ,给待查区间 [l,r]分段查询直到满足上面的可以直接返回的条件 int mid = (tree[rt].l + tree[rt].r) >> 1; if(l > mid){ ans += query(rt<<1|1, l , r); } else if(r <= mid){ ans += query(rt<<1, l , r); } else{ ans += query(rt<<1, l , mid) + query(rt<<1|1, mid+1 , r); } return ans; }
【完整代码】

#include<iostream> #include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int maxn = 1e5+100; struct node{ int l,r;//区间端点 int len;//区间长度 ll sum;//区间和 ll lazy;//懒标记 }tree[maxn<<2]; ll a[maxn]; //原数组 void pushUp(int rt){ tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum; } void build(int rt, int l, int r){ tree[rt].l = l;//左端点赋值 tree[rt].r = r;//右端点赋值 tree[rt].lazy = 0;//懒标记初始值记为0 tree[rt].len = r - l + 1;//区间长度赋值 if(l == r){//到了叶子节点 //tree[rt].sum = 1;//初始化为1 tree[rt].sum = a[l] ;//原来的数组a[] return; } int mid = (l + r) >> 1; build(rt<<1 , l, mid);//递归建立左子树 build(rt<<1|1, mid+1, r);//递归建立右子树 pushUp(rt);//回溯更新所有区间和 } void pushDown(int rt){ if(tree[rt].lazy){ //更新子节点的sum tree[rt<<1].sum += tree[rt].lazy * tree[rt<<1].len; tree[rt<<1|1].sum += tree[rt].lazy * tree[rt<<1|1].len; //下推标记 tree[rt<<1].lazy += tree[rt].lazy; tree[rt<<1|1].lazy += tree[rt].lazy; //根节点懒标记清零 tree[rt].lazy = 0; } } void update(int rt, int l , int r, int val){ //如果待更新区间[l,r]恰好是当前结点的区间则直接更新当前结点 if(tree[rt].l == l && tree[rt].r == r){ tree[rt].sum += val * tree[rt].len; tree[rt].lazy += val; return ; } //告诉我的左右孩子要更新了,爸爸已经更新了 pushDown(rt); int mid = (tree[rt].l + tree[rt].r) >> 1; // 递归更新 ,给待更新区间 [l,r]分段更新直到满足上面的可以直接更新的条件 if(l > mid){ update(rt<<1|1, l , r, val); } else if(r <= mid){ update(rt<<1, l , r, val); } else{ update(rt<<1, l , mid, val); update(rt<<1|1, mid+1 , r, val); } //向上保持正确 pushUp(rt); } ll query(int rt, int l , int r){ ll ans = 0; if(tree[rt].l ==l && tree[rt].r == r){ //如果待查区间[l,r]恰好是当前结点的区间则直接返回 return tree[rt].sum; } pushDown(rt);//下推懒标记告诉我的左右孩子要更新了 //递归查询 ,给待查区间 [l,r]分段查询直到满足上面的可以直接返回的条件 int mid = (tree[rt].l + tree[rt].r) >> 1; if(l > mid){ ans += query(rt<<1|1, l , r); } else if(r <= mid){ ans += query(rt<<1, l , r); } else{ ans += query(rt<<1, l , mid) + query(rt<<1|1, mid+1 , r); } return ans; } int main() { int n,m; scanf ("%d %d",&n,&m); for(int i=1; i<=n; i++){ scanf ("%lld",&a[i]); } build(1,1,n); int x,y,z; char op[3]; while(m--) { scanf ("%s",op); if (op[0] == ‘C‘) { scanf ("%d %d %d",&x,&y,&z); update(1,x,y,z); } else { scanf ("%d %d",&x,&y); printf ("%lld\n",query(1,x,y)); } } return 0; }
【规律总结】
线段树适用于区间查询和区间修改,但是它也具有一定的局限性。
(1)代码冗长,多处使用递归,很容易打错。
(2)查询的性质有限,只适用于满足区间加法的查询,比如查区间和,区间最大值最小值,区间GCD,等等,这些都是满足区间加法的。比如max(L,R) = max( max(L,K) , max(K,R) )
(3)规模不能太大。比如根区间有1e8这么长,这意味着什么,你的结构体数组要开4e8!够呛。所以需要离散化。什么是离散化呢?就是说你区间虽然有这么长,但是真正用到的很少,就几万个点,那么我需要重新编排一下,建立新的映射关系来建立线段树,具体分析和做法请见下一篇博文。
标签:tree splay 搜索 str 局限性 局限 lan 递归查询 printf
原文地址:https://www.cnblogs.com/czsharecode/p/9624422.html