标签:能量函数 sum div 关系 分享图片 基础上 进一步 icp img
这次主要介绍一种点云对齐的方法,多视数据最近迭代(ICP)对齐是最常用的点云对齐方法,为了提高对齐的精度及稳定性我们使用一种基于移动最小二乘(MLS)曲面的ICP多视数据对齐方法.该方法无需对数据进行额外的去噪和数据分割.对于优化噪声点的点云对齐可以采用本方法进行点云对齐。
因为扫面仪(传感器)的自身扫描范围限制,工业扫描往往不能一次对完整的模具进行扫描,需要通过多次转换视角进行模具的扫描.由于各视角的点云数据定义于各自的局部坐标系下,我们就需要对这些多视角测量数据进行坐标系转换使其在统一的坐标系下.
什么是点云对齐?
点云对齐就是通过坐标平移或旋转将具有相似特征的一组或几组点云转换到统一的全局坐标系下,多视角点云对齐通常有三类方法:
直接通过设备记录点云运动的方法成本太高,需要一台记录装置,本文主要针对目前使用最广的先进行手动粗对齐,在用IPC算法精对齐。
移动最小二乘(Moving Least-Squares,MLS)曲面逼近方法,不仅能适应任意拓扑形状的点云估计,而且逼近的MLS曲面具有良好的几何性质,可以通过确定逼近误差阈值排除噪点。
什么是MLS曲面?
国外研究者Levin将MLS曲面定义为满足对投影映射具有不变性的空间点集合,即
S(x) = {x∈R3|f(x) = x}
Amenta在次基础上对MLS曲面投影进行了更精确的定义。即沿法矢量场n(x)满足能量函数e(y,a)的极小值点集合(y为空间点,a为投影方向),并给出了由空间一点x0到MLS曲面的迭代投影计算方法。
如图1所示,从初始点xo开始沿加权法矢量n(xo)优化能量函数e(y,a)得到点x1,其中能量函数e(y,a)的定义为
\[{\rm{e}}\left( {{\rm{y}},{\rm{a}}} \right) = \mathop \sum \limits_{i = 1}^k {a^T} \bullet {\left( {y - pi} \right)^2}\theta \left( {y - pi} \right)\] (公式1)
公式1中:k为输入点y(如图1中的xi)的邻域点集{pi}的个数(一般k取15);a取输入点y处的加权法矢量n(xi),其中n(xi)可通过邻近点的加权平均得到,即
${\rm{n}}\left( {{{\rm{x}}_i}} \right) = \;\frac{{\mathop \sum \nolimits_{j = 1}^k {n_{{p_j}}}{v_j}}}{{\mathop \sum \nolimits_{j = 1}^k {n_{{p_j}}}{v_j}}}$ (公式2)
公式2中vj = ?(||xi-pi||)以及公式1中的vj = ?(||y-pi||)均为高斯函数,表示为
$\theta \left( {{\rm{xi}} - {\rm{pi}}} \right) = {e^{ - \frac{{{\rm{xi}} - {\rm{p}}{{\rm{i}}^2}}}{{{h^2}}}}}$ (公式3)
公式3中h为高斯函数的影响因子,取值较小时,MLS曲面比较靠近离散点云,但曲面不光滑;取值较大时,MLS曲面光滑,但在高曲率区域偏差增大,为获取光滑且偏差合适的MLS曲面,h可取点云数据中所有邻近点对间距离的平均值。
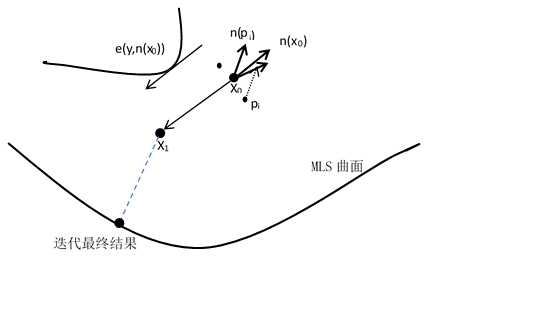
图1 计算MLS曲面图解
进一步对公式2求关于变量y的偏导,可以得到MLS曲面的隐式定义:
${\rm{g}}\left( {\rm{x}} \right) = {\rm{n}}\left( {\rm{x}} \right)\left( {\frac{{\partial \left( {e\left( {y,n\left( x \right)} \right)} \right)}}{{\partial y}}{|_{{\rm{\hat x}}}}} \right) = 0$
(公式4)
由上述MLS曲面的隐式定义及投影计算方法可知,MLS曲面实际为局部邻域点集的平滑逼近,具有很好的连续性及局部计算特性。由于单一或部分视角点云数据通常只覆盖工件部分区域,该区域MLS曲面应为非闭合曲面,其边界应为离散边界点集。
标签:能量函数 sum div 关系 分享图片 基础上 进一步 icp img
原文地址:https://www.cnblogs.com/xuhp/p/9649534.html