标签：分享   info   几何   意义   技术分享   总结   优化   例题   img   

例题引入

模板总结

对于此类方程：$ F[i]={min_{L(i) \leq j \leq R(i)}} \begin{Bmatrix} F[j]+val(i,j) \end{Bmatrix} $
暂时忽略min和范围得：$ F[i]=F[j]+val(i,j) $
整理得：$ F[j]=-val(i,j)+F[i] $
令$ -val(i,j)=f(i)*g(j)+h(i) $
则$ F[j]=f(i)*g(j)+F[i]+h(i) $
注意到对于每个确定的 $ i $ ，其 $ f(i) $ 和 $h(i) $ 值确定，即可看成常量，因此可以把 $ F[j] $ 看作 $ y $ ，把 $ f(i) $ 看作 $ a $ ，把 $ g(j) $ 看作 $ x $ ，把 $ F[i]+h(i) $ 看作 $ b $ ，则每一个决策可转化成求一个过点 $ (x,y) $ 的斜率已确定为 $ a $ 的直线 $ y=ax+b $ 的最小的截距 $ b $ ，也就求出了最小的 $ F[i] $ 。
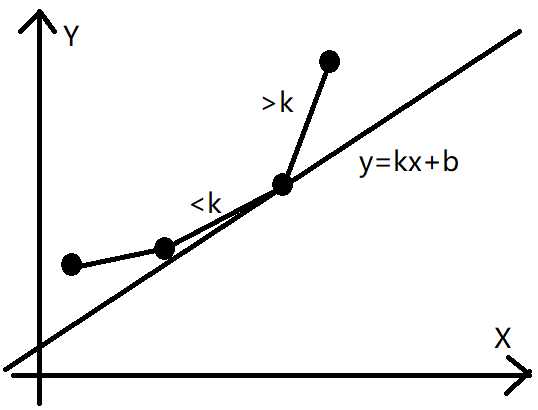
考虑其几何意义，如图，可以维护一个决策点的“下凸壳”，易知当直线的斜率处于下凸壳的两条相邻线段之间时决策最优。

一些可爱的坑

斜率优化总结

标签：分享   info   几何   意义   技术分享   总结   优化   例题   img   

原文地址：https://www.cnblogs.com/happyZYM/p/9650610.html