Matlab 符号运算

标签：style   blog   http   color   io   ar   strong   数据   sp   

• root(p)：多项式求根。多项式等于0时对应方程的根。

例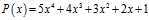：，则输入p=[5 4 3 2 1]; root(p)

• 注：多项式系数都是按幂指数递减形式的。

• poly([a,b,c])：求已知根为a,b,c所对应的多项式。

例：>>P1=ploy([2,3,4])

P1= 1 -9 26 -24 %即所求多项式为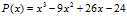

可以看出，root 和ploy互为逆运算。

• 注：ploy也可以求特征根。ploy(X)：即求矩阵X的特征根。

• ployval(p,a)：输出指定点x=a时的多项式值。
• conv(p,q)：多项式的乘法（卷积），p、q为两个多项式的系数。
• deconv(r,q)：多项式除法（解卷）
• [z,p,k]=residue(a,b)：部分分式。

例：分解函数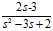 得到结果为：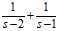

>> a=[2 -3]

b=[1 -3 2]

>>[z,p,k]=residue(a,b)

z =

1

1

p =

2

1

k =

[]

• ployder(P)：多项式求导（一阶导），输出一阶导数的系数
• ployfit(x,y,n)：多项式拟合（一般采用最小二乘拟合）。x,y是将要拟合的数据，n是要返回的多项式的阶数，最后输出的为多项式的系数。
• ployvalm(p,x)：矩阵多项式求值。p为多项式系数，x为矩阵，即求多项式在x时的值。
• collect(E,v)：合并同类项。合并表达式E中的v的同幂项系数合并。
• factor：因式分解。
• expand：符号表达式展开，多用于多项式、三角函数、指数函数、对数函数等的展开。
• simple、simplify：将符号表达式E综合化简。
• numden：表达式通分。[N,D]=numden(E)：分别返回分子N，分母D。
• findsym：确定自变量。findsym(f,n)确定符号函数f中的n个自变量，当指定n=1时，从符号函数f中找出在字母表中与x最近的字母。当输入参数n缺省时，函数命令将给出f中的所有的符号变量。
• conj：复数的共轭。
• polar(theta,rho):极坐标图像绘画。theta是用弧度制表示的角度，rho是对应的半径。

  ?

对象类型转化

double(C)：将符号(数值)常量C转化为双精度数值。

digits(D)：设置有效数字个数为D的近似解精度。

vpa(E,D)：求得符号表示式E的D位精度的数值解，返回的数值解也是符号对象类型。

numeric(E)：将不含变量的符号表达式E转化为double双精度浮点数值形式。其效果与double(sym(E))相同。

?

微积分运算

lim(F,x,a)：表达式F当变量xàa条件下的极限值。

lim(F,a)：表达式F中由函数命令findsym( )返回的独立变量趋向于a时的极限值。

lim(F)：符号函数或符号表达式F在x=0时的极限。

lim(F,x,a,‘right‘)：表达式F当变量xàa(从右趋向于a)条件下的极限值。

?

diff(f,‘v‘,n)：对表达式或函数f指定的自变量v计算其n阶导数。

int(S,v)：计算符号函数或表达式S对指定符号变量v的不定积分。输出积分结果不显示积分常数C。

int(S,v,a,b)：计算符号函数或表达式S对指定符号变量v的定积分，积分区间[a,b]。

?

求和函数与泰勒级数展开

symsum(S,v,a,b)：输入对象函数或表达式S，在对指定变量v取遍[a,b]所有的整数时，对函数S求和，最后输出级数的和。

taylor(f,x)：将输入函数f展开成泰勒级数，求其5次幂的近似多项式。输入参数无x时，函数f的变量由findsym( )确定。

taylor(f,‘order‘,n)：将输入函数f展开成泰勒级数，求其n-1次幂的近似多项式。

taylor(f,c,n)：将输入函数f展开成x-c的泰勒级数，求其5次幂的近似多项式。

taylor(f,‘ ExpansionPoint‘,a)：将输入函数f展开成在a点附近的泰勒级数，求其5次幂的近似多项式。

?

矩阵的微分与积分

jacobian(f,v)：输入参量f是列向量函数f(v)，输入参量v是行向量，输出矩阵为雅克比矩阵。

[V,J]=jordan(A)：输出矩阵J是矩阵A的约当标准型矩阵。参量V满足J=V\A·V=V^-1·A·V。

?

方程的求解

• S=solve(‘eqn1‘, ‘eqn2‘, …,‘eqnN‘, ‘v1‘, ‘v2‘,…, ‘vN‘)：对方程组指定变量，联立求解。
• solve(‘eqn1‘, ‘eqn2‘, …,‘eqnN‘)

  S=solve(‘eqn1‘, ‘eqn2‘, …,‘eqnN‘)

  [v1, v2,…, vN]=solve(‘eqn1‘, ‘eqn2‘, …,‘eqnN‘)：输入参数无指定变量部分。

• S=dsolve(‘eqn1‘, ‘eqn2‘, …,‘初始条件部分‘, ‘指定独立变量部分‘)：求解常微分方程

  当y为因变量时，用Dny表示y的n阶导函数。

  初始或者边界条件y|_x=a=b与y‘|_x=c=d分别写成y(a)=b与Dy(c)=d。

  例：求解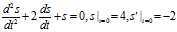

  >> syms x y;

  >> s=dsolve(‘D2s+2*Ds+s=0‘,‘s(0)=4,Ds(0)=-2‘,‘t‘);

  >> s=simple(factor(s))

  s =

  2*exp(-t)*(t + 2)

?

Matlab 符号运算

标签：style   blog   http   color   io   ar   strong   数据   sp   

原文地址：http://www.cnblogs.com/lingsui/p/4012210.html