标签:style blog http color io ar strong sp 2014
1.间隔(Margins)
考虑逻辑回归,概率值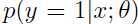 是由模型
是由模型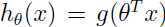 预测出来的,给定
预测出来的,给定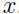 ,如果
,如果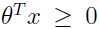 ,则
,则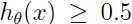 ,预测最终类别就为1.
,预测最终类别就为1.
对于一个正类样本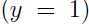 ,
,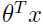 越大,
越大,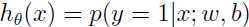 也就越大,我们也就更大程度上确定该样本属于类别1.也就是说如果
也就越大,我们也就更大程度上确定该样本属于类别1.也就是说如果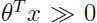 ,那么预测
,那么预测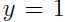 就非常可信,类似地,如果
就非常可信,类似地,如果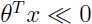 ,我们就能很自信
,我们就能很自信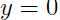 是正确的预测.换种角度,对于给定的训练集,如果我们拟合出合适的参数
是正确的预测.换种角度,对于给定的训练集,如果我们拟合出合适的参数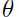 ,对于任何一正类样本
,对于任何一正类样本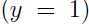 ,使得
,使得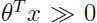 ,对于任何负类样本(
,对于任何负类样本(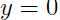 ),使得
),使得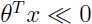 ,那么就可以说拟合出了很好的参数,因为这个参数对应的分类器可以将样本很“自信”地区分开来,如果拟合出侧参数使得
,那么就可以说拟合出了很好的参数,因为这个参数对应的分类器可以将样本很“自信”地区分开来,如果拟合出侧参数使得 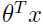 = 0,这就使得
= 0,这就使得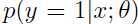 =0,也就是说很难确定到底是哪一类,也就是参数使得
=0,也就是说很难确定到底是哪一类,也就是参数使得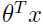 的值距离0越远越好,这样就越加容易确定出给定特征所属类别。
的值距离0越远越好,这样就越加容易确定出给定特征所属类别。
考虑下面的图:
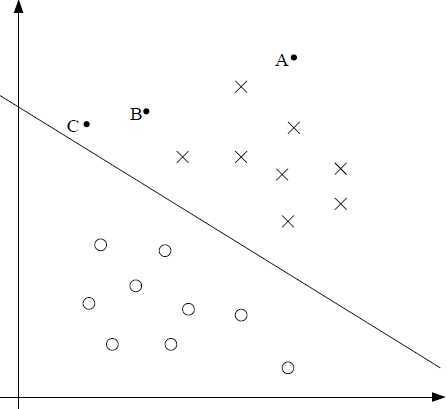
上面的直线就是决策边界(也叫分割超平面)根据所得A,B,C是三个已经被分出类的点。注意到,点A距离决策边界很远,如果被问对于A的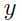 值得预测是多少,我们可以很大胆且自信的说
值得预测是多少,我们可以很大胆且自信的说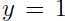 .反观点C,距离决策边界很近,虽然我们根据当前的决策边界也预测
.反观点C,距离决策边界很近,虽然我们根据当前的决策边界也预测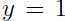 ,但是当决策边界作出很小的改变,就很容易使得
,但是当决策边界作出很小的改变,就很容易使得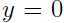 ,因此我们对A的预测比对C的预测更加自信,也就是说如果某点距离决策边界越远,那么根据此决策边界对该点作出的预测就更加可信。
,因此我们对A的预测比对C的预测更加自信,也就是说如果某点距离决策边界越远,那么根据此决策边界对该点作出的预测就更加可信。
2.符号标记
为了使得讨论SVM更加清晰,首先来介绍一些符号标记。我们将用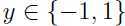 来表示正负类,用
来表示正负类,用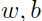 来表示参数,我们要学习出的分类器模型如下:
来表示参数,我们要学习出的分类器模型如下:
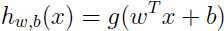
其中,如果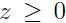 ,
,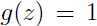 ,否则
,否则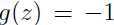
3.函数间隔和几何间隔(Functional and geometric margins)
给定某一训练样本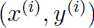 ,我们定义的关于参数
,我们定义的关于参数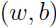 函数间隔:
函数间隔:
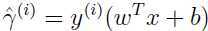 .
.
如果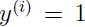 ,为了让函数间隔较大(正如前面讨论,为了预测更加可信和正确),需要
,为了让函数间隔较大(正如前面讨论,为了预测更加可信和正确),需要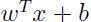 是一个很大的正值,当
是一个很大的正值,当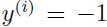 ,
,
同样为了让函数间隔较大,就需要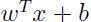 是一个绝对值很大的负值。简单来说,当
是一个绝对值很大的负值。简单来说,当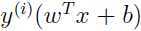 是一个很大的正值时,我们对样本的预测的正确性就会相当大,因此一个较大的函数间隔就意味着更加可信和正确的预测。然而增大
是一个很大的正值时,我们对样本的预测的正确性就会相当大,因此一个较大的函数间隔就意味着更加可信和正确的预测。然而增大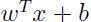 绝对值得方法其实很简单,用
绝对值得方法其实很简单,用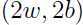 代替
代替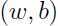 就很容易达到目的,但这样做真的可行或者有意义吗?考虑下面的讨论。
就很容易达到目的,但这样做真的可行或者有意义吗?考虑下面的讨论。
对于一个线性分类器,我们选择上面提到的函数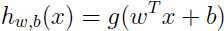 (只能取1或者-1),如果我们用
(只能取1或者-1),如果我们用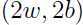 代替
代替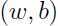 ,显然有
,显然有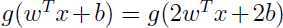 ,也就是说
,也就是说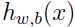 的值就没变,即
的值就没变,即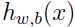 只取决于
只取决于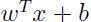 的符号,而不是
的符号,而不是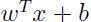 值的大小。但是,用
值的大小。但是,用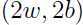 代替
代替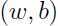 后,导致上面提到的函数间隔
后,导致上面提到的函数间隔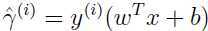 也变为原来的两倍。但是,如果原来预测
也变为原来的两倍。但是,如果原来预测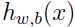 =0.5,就是
=0.5,就是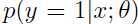 =0.5,意味着是1或者-1类的几率是一样的,很难确定到底是哪一类,即使代替后函数间隔变为原来的2倍,由于
=0.5,意味着是1或者-1类的几率是一样的,很难确定到底是哪一类,即使代替后函数间隔变为原来的2倍,由于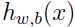 没变,所以还是很难确定,所以增大函数间隔后并没有提高预测的可信度和准确性,那么之前说的“一个较大的函数间隔就意味着更加可信和正确的预测”是不是有问题呢?显然是有问题的,所以为了解决这个问题,我们得从函数间隔的定义入手:采取一种归一化手段,令
没变,所以还是很难确定,所以增大函数间隔后并没有提高预测的可信度和准确性,那么之前说的“一个较大的函数间隔就意味着更加可信和正确的预测”是不是有问题呢?显然是有问题的,所以为了解决这个问题,我们得从函数间隔的定义入手:采取一种归一化手段,令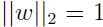 ,用
,用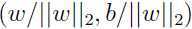 代替
代替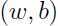 。后面会继续讨论这个问题。
。后面会继续讨论这个问题。
给定训练集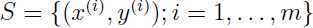 ,前面
,前面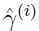 是代表训练集中某一个样本的函数间隔,我们定义训练集的函数间隔是训练集中所有样本的函数间隔中最小的那个,用
是代表训练集中某一个样本的函数间隔,我们定义训练集的函数间隔是训练集中所有样本的函数间隔中最小的那个,用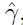 表示训练集的函数间隔,则根据定义:
表示训练集的函数间隔,则根据定义:
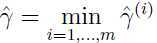
下面讨论几何间隔,考虑下面图片:
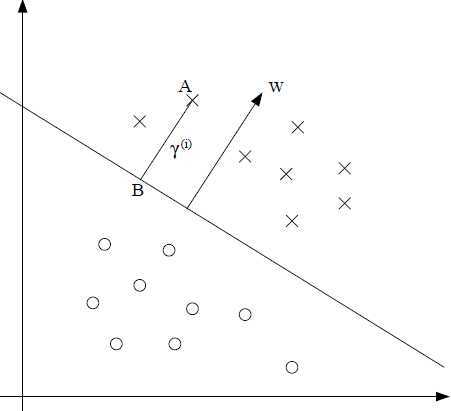
在参数还是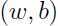 的情况下决策边界如上面直线所示。因为决策边界的方程是
的情况下决策边界如上面直线所示。因为决策边界的方程是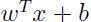 =0,根据几何知识可以知道,决策边界是与向量
=0,根据几何知识可以知道,决策边界是与向量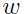 垂直的。考虑点A代表着某个训练样本
垂直的。考虑点A代表着某个训练样本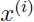 被标记为1类,点A到决策边界的距离就是线段AB的长度,用
被标记为1类,点A到决策边界的距离就是线段AB的长度,用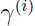 表示,注意区别于
表示,注意区别于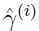 。
。
如何计算出A的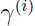 值呢?可以看出
值呢?可以看出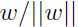 是与
是与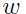 同向的单位向量,A代表
同向的单位向量,A代表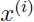 ,因此点B就可以表示为
,因此点B就可以表示为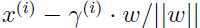
但是点B是决策边界上的一点,根据决策边界的方程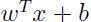 =0可以得到:
=0可以得到:
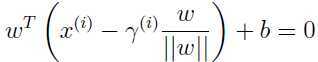
解出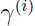 :
:
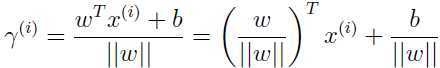
然而这只是位于决策边界上方的正样本的,更加一般地,我们定义出任意训练集中的样本的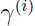 :
:
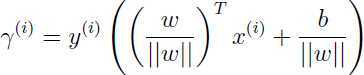
这就是任意样本的几何间隔(geometric margin).
当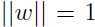 ,函数间隔就和几何间隔相等,这就将两种不同间隔联系了起来。
,函数间隔就和几何间隔相等,这就将两种不同间隔联系了起来。
但是,当我们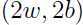 用代替
用代替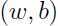 ,函数间隔会变为原来的2倍,而几何间隔却不会变(这个在后面性质会很有用),
,函数间隔会变为原来的2倍,而几何间隔却不会变(这个在后面性质会很有用),
这就解释了为什么前面用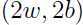 代替
代替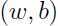 ,函数间隔变大,而分类准确度和可信度没有变化,因为函数间隔虽然变大,但是反映到实际的图形中,我们可以看到该点到分类边界的距离
,函数间隔变大,而分类准确度和可信度没有变化,因为函数间隔虽然变大,但是反映到实际的图形中,我们可以看到该点到分类边界的距离 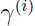 (几何间隔)并没有变化,分类准确度和可信度当然不会提高,所以函数间隔存在局限性,而几何间隔就不存在这种问题,只要几何间隔变大,在图形中很显然就可以反映出分类可信度的提高。
(几何间隔)并没有变化,分类准确度和可信度当然不会提高,所以函数间隔存在局限性,而几何间隔就不存在这种问题,只要几何间隔变大,在图形中很显然就可以反映出分类可信度的提高。
最后定义出训练集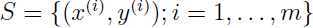 的几何间隔,就是所有样本个体的几何间隔最小的间隔:
的几何间隔,就是所有样本个体的几何间隔最小的间隔:
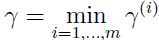
4.最佳间隔分类器
根据之前的讨论,在给定训练集的情况下,最重要是找到一个决策边界最大化该训练集的几何间隔,最终的分类结果就是,几何间隔就像一条河沟一样,一边是正类,另一边是负类。
现在假设给定的训练集是线性可分的,即可以用超平面将样本分成正负类。那么如何得到最大几何间隔呢?于是自然我们想到优化下面的问题:
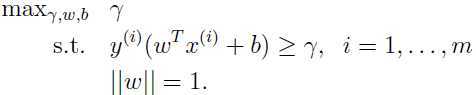
第一个约束保证所有函数间隔都至少为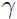 ,
,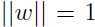 进一步保证函数间隔和几何间隔相等(为了解决上面讨论过的函数间隔的局限性),这样就保证了所有几何间隔都至少为
进一步保证函数间隔和几何间隔相等(为了解决上面讨论过的函数间隔的局限性),这样就保证了所有几何间隔都至少为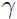 .优化这个问题,我们就可以得到最大几何间隔时的参数
.优化这个问题,我们就可以得到最大几何间隔时的参数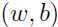 .
.
由于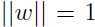 的限制,使得上述优化的问题,变成了一个非凸的问题,就很用常规的解析的方法去优化,于是把问题转换一下,由前面讨论可知,函数间隔和几何间隔有如下关系:
的限制,使得上述优化的问题,变成了一个非凸的问题,就很用常规的解析的方法去优化,于是把问题转换一下,由前面讨论可知,函数间隔和几何间隔有如下关系:
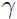 =
=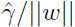
于是优化问题可以转换为:
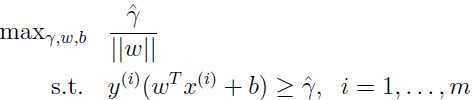
然而, 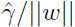 仍然是一个非凸目标,下面继续
仍然是一个非凸目标,下面继续
回想我们之前说过,对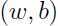 随意扩大或者缩小任意倍数对最终分类的性能是没有什么影响的,下面就要利用这一点。
随意扩大或者缩小任意倍数对最终分类的性能是没有什么影响的,下面就要利用这一点。
我们限制含有参数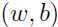 的函数间隔必须为1:
的函数间隔必须为1:
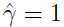
于是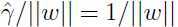 ,而最大化
,而最大化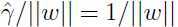 和最小化
和最小化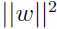 是等价的,
是等价的,
于是问题进一步转化:
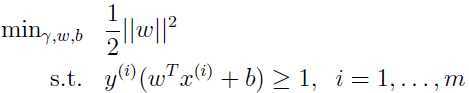
成功转化非凸目标到一个可解析的凸目标,而且只有一个线性约束,它的解就是最佳间隔分类器。
传统的二次规划就可以解决这个问题。但是当问题维数是在高维的时候,二次规划的效率就成了一个问题,为了解决这个问题,引入拉格朗日对偶(Lagrange duality)
5.拉格朗日对偶(Lagrange duality)
下面讨论注重思想,不要在意公式。
考虑下面问题:
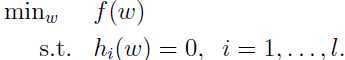
转化为无约束问题求解:定义拉格朗日算子:
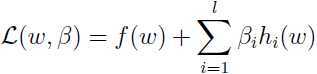
这里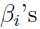 是拉格朗日乘子,对拉格朗日算子求偏导并让导数为0:
是拉格朗日乘子,对拉格朗日算子求偏导并让导数为0:
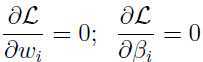
解出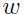 和
和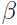 .
.
上面的问题只有一个等式约束,下面讨论更为一般的既含有等数约束,又含有不等式约束。
定义一个原问题:
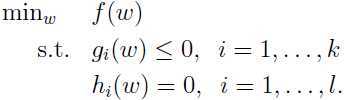
类似与上面问题的求解方式,定义一个拉格朗日算子:
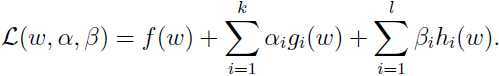
这里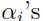 和
和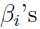 都是拉格朗日乘子.
都是拉格朗日乘子.
考虑下面数值:
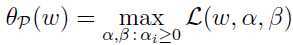
假如给定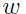 ,假如
,假如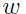 不满足原约束条件,即
不满足原约束条件,即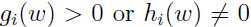 ,
,
那么:
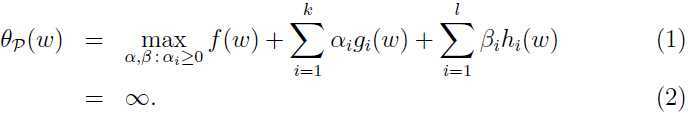
相反,如果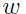 满足原约束条件,那么:
满足原约束条件,那么:
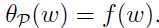
由此可见,在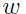 满足原约束条件下,
满足原约束条件下,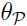 和我们所要解决的问题目标有着相同的值,如
和我们所要解决的问题目标有着相同的值,如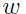 不满足原约束条件,
不满足原约束条件,
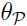 就趋向正无穷.于是我们发现下面等式成立:
就趋向正无穷.于是我们发现下面等式成立:
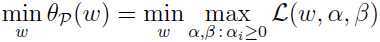
于是定义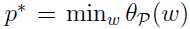 ,称为原问题的目标值.
,称为原问题的目标值.
现在来讨论一个稍微有些不同问题:
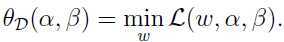
注意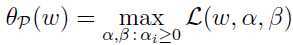 是最大化给定
是最大化给定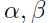 的目标,而这问题是最小化给定
的目标,而这问题是最小化给定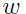 的目标.
的目标.
由此得到如问题,称为对偶问题:
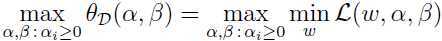 ,
,
回头看看原问题: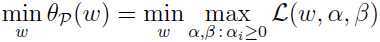 ,可以发现,原问题和对偶问题除了“max”和“min”
,可以发现,原问题和对偶问题除了“max”和“min”
交换了位置之外,其余的完全一样.
同样,我们定义对偶问题的目标值: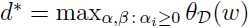 .
.
于是,可以得出对偶问题和原问题的关系:
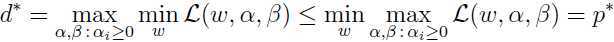 (函数极小值的极大值肯定小于极大值的极小值)
(函数极小值的极大值肯定小于极大值的极小值)
但是,在一定条件下有:
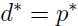
所以,在这个条件成立的时候,有时为了方便,我们可以解原问题的对偶问题而不去直接解原问题。下面讨论原问题和对偶问题目标值相等的条件。
将最初的问题再写出来:
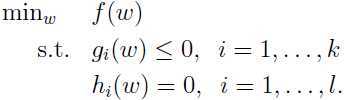
假设函数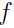 和约束条件
和约束条件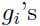 都是凸函数,约束条件
都是凸函数,约束条件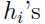 是线性函数(即存在
是线性函数(即存在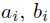 使得
使得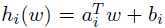 成立),进一步假设
成立),进一步假设
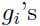 是严格可行,对于所有
是严格可行,对于所有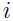 即至少存在一个
即至少存在一个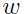 使得
使得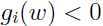 .
.
在上述假设条件下,一定存在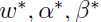 ,使得
,使得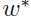 是原问题
是原问题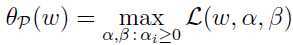 的解,
的解,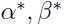 是对偶问题
是对偶问题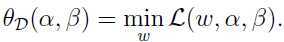 的解,并且
的解,并且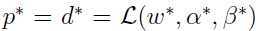 .此外,
.此外,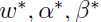 满足KKT条件(Karush-Kuhn-Tucker conditions):
满足KKT条件(Karush-Kuhn-Tucker conditions):
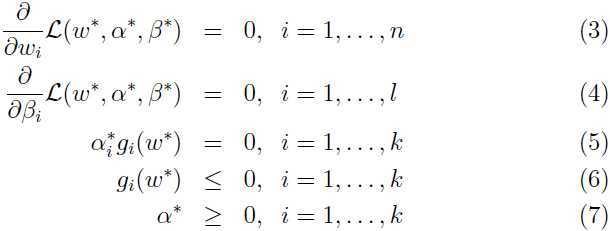
总的来说,如果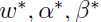 满足KKT条件,原问题的解就和对偶问题的解相等.
满足KKT条件,原问题的解就和对偶问题的解相等.
特别注意条件(5)是对偶互补条件,它意味着如果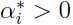 ,则
,则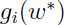 =0,这将会成为后面讨论的一个关键.
=0,这将会成为后面讨论的一个关键.
6.最佳间隔分类器(续4)
在第4部分,为了找到最佳间隔分类器,采取优化下面的问题(原问题):
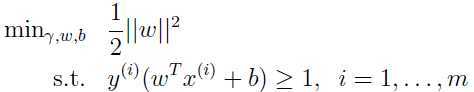
为和第5部分讨论的优化问题形式上统一,可以把这个优化问题的约束条件写为:
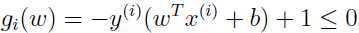
由KKT对偶互补条件可知:αigi(ω)=0,又由KKT条件可知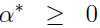 ,这里就是αi≥0.如果αi>0,则gi(ω)=0,即
,这里就是αi≥0.如果αi>0,则gi(ω)=0,即
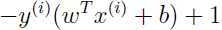 = 0,于是
= 0,于是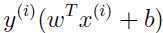 =1,而
=1,而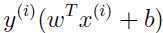 就是样本
就是样本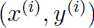 的函数间隔.由此可知,只有当样本函数间隔为1时,才有
的函数间隔.由此可知,只有当样本函数间隔为1时,才有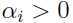 .
.
考虑下面的示意图:
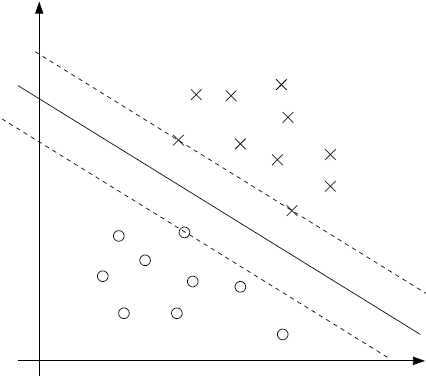
实线代表最大间隔分割超平面.最靠近决策边界的点的间隔最小,有三个点(两个正样本和一个负样本)正好位于与决策边界平行的虚线上。由于在原问题的约束中规定了间隔为1,所以间隔为1的点只有3个,由前面讨论可知使得αi>0的点只有这三个,那么这三个点就是这个问题的支持向量(support vectors).可以看出支持向量的数目要远比训练样本数目小.
下面我们试图用对偶的方法解这个问题,构造原问题的拉格朗日算子:
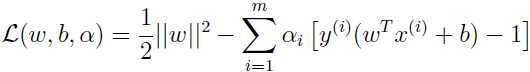
根据KKT条件:
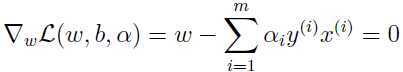
于是得到: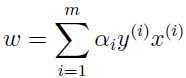
于是拉格朗日算子可以写为:
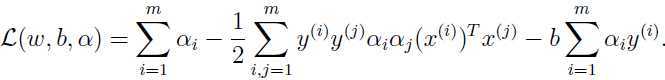
同样有KKT条件:
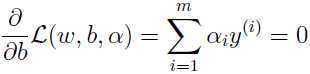
进一步简化:
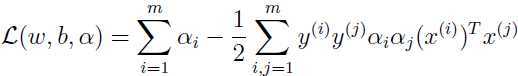
于是得到对偶问题:
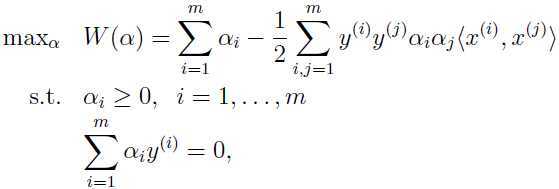
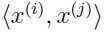 表示:
表示: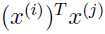
如何解这个对偶问题暂时不谈,假如已经解出了这对偶问题,得到了最优的α,那么根据上面的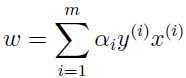 ,
,
就可以得到最佳的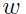 ,即找到了
,即找到了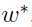 ,然后由下面的等式:
,然后由下面的等式:
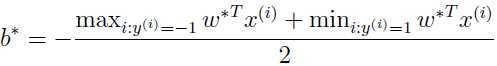
得到最优的b,即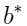 .
.
假设根据训练集现在已经拟合出了各个参数,对于新来的输入点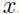 ,我们通过计算
,我们通过计算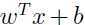 ,当且仅当这个值大于0时,给出预测
,当且仅当这个值大于0时,给出预测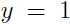 ,而根据
,而根据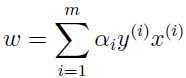 :
:
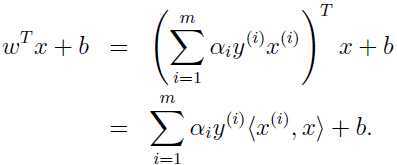
因此,如果已经拟合出α,为了计算这个值只需要计算训练集中的点和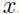 的内积即可.由上面的讨论可知,除了支持向量对应的几个点对应的α不为0,其余情况下α均为0.所以累加的许多项都为0,我们只需计算出支持向量(往往数量很少)和
的内积即可.由上面的讨论可知,除了支持向量对应的几个点对应的α不为0,其余情况下α均为0.所以累加的许多项都为0,我们只需计算出支持向量(往往数量很少)和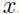 的内积即可.
的内积即可.
标签:style blog http color io ar strong sp 2014
原文地址:http://www.cnblogs.com/90zeng/p/SVM.html