与平面和空间打交道的计算几何

时间：2018-09-18 23:54:14 阅读：231 评论：0 收藏：0 [点我收藏+]

标签：val 部分 element journey 字典 ping play ble 方便

计算几何基础

Jack Straws(POJ 1127)

原题如下：
Jack Straws

Time Limit: 1000MS Memory Limit: 10000K

Total Submissions: 5494 Accepted: 2504

Description

In the game of Jack Straws, a number of plastic or wooden "straws" are dumped on the table and players try to remove them one-by-one without disturbing the other straws. Here, we are only concerned with if various pairs of straws are connected by a path of touching straws. You will be given a list of the endpoints for some straws (as if they were dumped on a large piece of graph paper) and then will be asked if various pairs of straws are connected. Note that touching is connecting, but also two straws can be connected indirectly via other connected straws.

Input

Input consist multiple case,each case consists of multiple lines. The first line will be an integer n (1 < n < 13) giving the number of straws on the table. Each of the next n lines contain 4 positive integers,x1,y1,x2 and y2, giving the coordinates, (x1,y1),(x2,y2) of the endpoints of a single straw. All coordinates will be less than 100. (Note that the straws will be of varying lengths.) The first straw entered will be known as straw #1, the second as straw #2, and so on. The remaining lines of the current case(except for the final line) will each contain two positive integers, a and b, both between 1 and n, inclusive. You are to determine if straw a can be connected to straw b. When a = 0 = b, the current case is terminated.

When n=0,the input is terminated.

There will be no illegal input and there are no zero-length straws.

Output

You should generate a line of output for each line containing a pair a and b, except the final line where a = 0 = b. The line should say simply "CONNECTED", if straw a is connected to straw b, or "NOT CONNECTED", if straw a is not connected to straw b. For our purposes, a straw is considered connected to itself.

Sample Input
```
7
1 6 3 3 
4 6 4 9 
4 5 6 7 
1 4 3 5 
3 5 5 5 
5 2 6 3 
5 4 7 2 
1 4 
1 6 
3 3 
6 7 
2 3 
1 3 
0 0

2
0 2 0 0
0 0 0 1
1 1
2 2
1 2
0 0

0
```
Sample Output
```
CONNECTED 
NOT CONNECTED 
CONNECTED 
CONNECTED 
NOT CONNECTED 
CONNECTED
CONNECTED
CONNECTED
CONNECTED
```
分析：问题的关键是判断线段是否相交，然后就可以建图进行连接性判断。首先会想到计算两直线的交点然后判断交点是否在线段上的方法，这样问题就变成如何判断点是否在线段上以及如何求两直线的交点。在几何问题中，运用向量的内积和外积进行计算是非常方便的。对于二维向量p₁=(x₁,y₁)和p₂=(x₂,y₂)，定义内积p₁·p₂=x₁x₂+y₁y₂，外积p₁×p₂=x₁y₂-y₁x₂。要判断点q是否在线段p₁-p₂上，只要先根据外积(p₁-q)×(p₂-q)是否等于0来判断点q是否在直线p₁-p₂上，再利用内积(p₁-q)·(p₂-q)是否小于等于0来判断点q是否落在p₁-p₂之间。而要求两直线的交点，通过变量t将直线p₁-p₂上的点表示为p₁+t(p₂-p₁)，交点又在直线q₁-q₂上，所以有：(q₂-q₁)×(p₁+t(p₂-p₁)-q₁)=0，于是可以利用下式求得t的值：

但是，使用这个方法还要注意边界情况，如果两条线段是平行的，也有可能有公共点，可以通过检查端点是否在另一条线段上来判断。

代码：

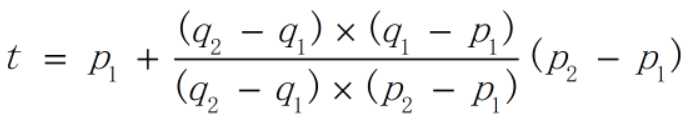
  1 #include <cstdio>
  2 #include <cmath>
  3 #include <algorithm>
  4 
  5 using namespace std;
  6 
  7 const double EPS=1e-10;
  8 
  9 double add(double a, double b)
 10 {
 11     if (fabs(a+b)<EPS*(fabs(a)+fabs(b))) return 0;
 12     return a+b;
 13 }
 14 
 15 struct P
 16 {
 17     double x,y;
 18     P(){};
 19     P(double x, double y):x(x),y(y){}
 20     P operator + (P p)
 21     {
 22         return P(add(x, p.x), add(y, p.y));
 23     }
 24     P operator - (P p)
 25     {
 26         return P(add(x, -p.x), add(y, -p.y));
 27     }
 28     P operator * (double d)
 29     {
 30         return P(x*d, y*d);
 31     }
 32     double dot(P p)
 33     {
 34         return add(x*p.x, y*p.y);
 35     }
 36     double det(P p)
 37     {
 38         return add(x*p.y, -y*p.x);
 39     }
 40 };
 41 
 42 bool on_seg(P p1, P p2, P q)
 43 {
 44     return (p1-q).det(p2-q)==0 && (p1-q).dot(p2-q)<=0;
 45 }
 46 
 47 P intersection(P p1, P p2, P q1, P q2)
 48 {
 49     return p1+(p2-p1)*((q2-q1).det(q1-p1)/(q2-q1).det(p2-p1));
 50 }
 51 
 52 const int MAX_N=15;
 53 const int MAX_M=2000;
 54 int n;
 55 P p[MAX_N], q[MAX_N];
 56 int m;
 57 int a[MAX_M], b[MAX_M];
 58 bool g[MAX_N][MAX_N]; 
 59 
 60 int main()
 61 {
 62     while (~scanf("%d", &n) && n)
 63     {
 64         fill(g[0], g[0]+sizeof(bool)*15*15, false);
 65         for (int i=0; i<n; i++)
 66         {
 67             scanf("%lf %lf %lf %lf", &p[i].x, &p[i].y, &q[i].x, &q[i].y);
 68         }
 69         for (int i=0;;i++)
 70         {
 71             scanf("%d %d",&a[i], &b[i]);
 72             if (a[i]==0 && b[i]==0)
 73             {
 74                 m=i;
 75                 break;
 76             }
 77         }
 78         for (int i=0; i<n; i++)
 79         {
 80             g[i][i]=true;
 81             for (int j=0; j<i; j++)
 82             {
 83                 if ((p[i]-q[i]).det(p[j]-q[j])==0)
 84                 {
 85                     g[i][j]=g[j][i]=on_seg(p[i], q[i], p[j])
 86                                  || on_seg(p[i], q[i], q[j])
 87                                  || on_seg(p[j], q[j], p[i])
 88                                  || on_seg(p[j], q[j], q[i]);
 89                 }
 90                 else
 91                 {
 92                     P r=intersection(p[i], q[i], p[j], q[j]);
 93                     g[i][j]=g[j][i]=on_seg(p[i], q[i], r) && on_seg(p[j], q[j], r);
 94                 }
 95             }
 96         }
 97         for (int k=0; k<n; k++)
 98             for (int i=0; i<n; i++)
 99                 for (int j=0; j<n; j++)
100                 {
101                     g[i][j] |= g[i][k]&&g[k][j]; 
102                 } 
103         for (int i=0; i<m; i++)
104         {
105             puts(g[a[i]-1][b[i]-1] ? "CONNECTED" : "NOT CONNECTED");
106         }
107     }
108 }

Jack Straw

注：几何问题中需要特别注意处理边界情况和避免分类讨论时产生疏漏。具有代表性的边界情况有：
①两直线平行、三点共线、除零的情况
②将所有点排序后处理时，弄错了对相同x坐标或y坐标的点的处理顺序
③判断直线和多边形是否相交时，漏掉了直线恰好通过多边形顶点的情况
④判断两个实心物体是否相交时，忘记了其中一个完全在另一个内部的情况
⑤在物体移动的模拟类问题中，将初始相接触但随后分离的情况误判为碰撞
此外，求解几何问题时往往用到浮点数，要注意误差问题。
事实上，判断线段相交时，通常不用前面这样利用两直线交点的方法，而是利用基于ccw(Counter Clock Wise)函数的方法，另外可以把C++ Standard Library的Complex类当作二维向量使用，这样就不用自己实现各种运算且容易完成各类操作。
这里介绍了如果求两直线的交点，此外也有需要求直线同圆的交点或是两个圆的公切线之类的情况。

计算误差

对于double类型，尾数部分大致相当于10进制下的15位，多数情况下，就其计算结果而言，精度已经足够了，但当我们要比较两个计算后的结果时，就需要特别注意。由于误差，原本应该相等的结果有可能实际上并不相等。比较包含舍入误差的浮点数时所采用的方法，一般是选取合适的足够小的常数EPS，按如下规则处理：

a<0→a<-EPS

a<=0→a<EPS

a==0→fabs(a)<EPS

在大多数计算结果不是太大的情况下，都可以使用该方法处理。在比较大的结果时要格外注意，假设所取的EPS为10^-10,现在要求对因为误差导致原本相等却实际不等的大约10⁸大小的两个数作差，并判断是否等于0，由于double的精度只有约十进制15位，所得差的绝对值将大于EPS，所以会被误判为不等。像这样，求两个非常接近的数的差时会发生有效位丢失，导致所得结果的有效数字位数大大减少。前面的程序所用的方法是，在进行浮点数减法时，如果两个数按相对误差比较是相等的就另结果为0，这样我们在计算的过程中处理了误差，所以在与0进行比较时，就可以不考虑误差直接比较了。

极限情况

White Bird (AOJ 2308)

原题如下：
Angry Birds is a mobile game of a big craze all over the world. You were convinced that it was a waste of time to play the game, so you decided to create an automatic solver.

You are describing a routine that optimizes the white bird‘s strategy to defeat a pig (enemy) by hitting an egg bomb. The white bird follows a parabolic trajectory from the initial position, and it can vertically drop egg bombs on the way.

In order to make it easy to solve, the following conditions hold for the stages.
- N obstacles are put on the stage.
- Each obstacle is a rectangle whose sides are parallel to the coordinate axes.
- The pig is put on the point (X, Y).
- You can launch the white bird in any direction at an initial velocity V from the origin.
- If the white bird collides with an obstacle, it becomes unable to drop egg bombs.
- If the egg bomb collides with an obstacle, the egg bomb is vanished.
The acceleration of gravity is 9.8 {\rm m/s^2}. Gravity exerts a force on the objects in the decreasing direction of y-coordinate.

Input

A dataset follows the format shown below:

NVXY
L_1B_1R_1T_1
...
L_NB_NR_NT_N

All inputs are integer.
- N: the number of obstacles
- V: the initial speed of the white bird
- X, Y: the position of the pig
(0 \leq N \leq 50, 0 \leq V \leq 50, 0 \leq X, Y \leq 300, X \neq 0)

for 1 \leq i \leq N,
- L_i: the x-coordinate of the left side of the i-th obstacle
- B_i: the y-coordinate of the bottom side of the i-th obstacle
- R_i: the x-coordinate of the right side of the i-th obstacle
- T_i: the y-coordinate of the top side of the i-th obstacle
(0 \leq L_i, B_i, R_i, T_i \leq 300)

It is guaranteed that the answer remains unaffected by a change of L_i, B_i, R_i and T_i in 10^{-6}.

Output

Yes/No

You should answer whether the white bird can drop an egg bomb toward the pig.

Sample Input 1
```
0 7 3 1
```
Output for the Sample Input 1
```
Yes
```
Sample Input 2
```
1 7 3 1
1 1 2 2
```
Output for the Sample Input 2
```
No
```
Sample Input 3
```
1 7 2 2
0 1 1 2
```
Output for the Sample Input 3
```
No
```
分析：最后的限制条件常常会在几何问题中附带出现，根据这一点就无需考虑只有通过像穿过针孔一样的唯一线路才能让卵击中猪的情况了。首先，让我们考虑一下如何判断以某个角度射出的鸟是否可以产卵击中猪。只要射出的鸟在撞到障碍物之前能够从猪的正上方飞过，并且此时与猪之间没有障碍物的话，在正上方产卵就可以击中猪了。判断白鸟是否撞到障碍物，就是判断抛物线和长方形是否相交（如果将长方形分解为线段，只判断抛物线是否同各条线段相交，就可能无法很好地处理抛物线恰好经过长方形的顶点的情况）。接下来，思考一下如何枚举所有关键射出角度，假设以某个角度射出时不会遇到障碍物，我们逐渐降低这个角度，直到某出变成
① 恰好经过(X,Y)
② 恰好经过某个障碍物的左上角或右上角
就不能再降低了。虽然作为解的角度可能有无穷多个，但因为无论哪个都可以不断降低直至变为1或2的情况，所以只要检查这些角度就足够了。

代码：

 1 #include <cstdio>
 2 #include <cmath>
 3 
 4 using namespace std;
 5 
 6 const double EPS=1e-10;
 7 const int MAX_N=1000;
 8 const double g=9.8;
 9 int N,V,X,Y;
10 int L[MAX_N], B[MAX_N], R[MAX_N], T[MAX_N];
11 
12 double calc(double vy, double t)
13 {
14     return vy*t-g*t*t/2;
15 }
16 
17 int cmp(double lb, double ub, double a)
18 {
19     return a<lb+EPS ? -1 : a>ub-EPS ? 1 : 0;
20 }
21 
22 bool check(double qx, double qy)
23 {
24     double a=g*g/4, b=g*qy-V*V, c=qx*qx+qy*qy;
25     double D=b*b-4*a*c;
26     if (D<0 && D>-EPS) D=0;
27     if (D<0) return false;
28     for (int d=-1; d<=1; d+=2)
29     {
30         double t2=(-b+d*sqrt(D))/(2*a);
31         if (t2<=0) continue;
32         double t=sqrt(t2);
33         double vx=qx/t, vy=(qy+g*t*t/2)/t;
34         double yt=calc(vy, X/vx);
35         if (yt<Y-EPS) continue;
36         bool ok=true;
37         for (int i=0; i<N; i++)
38         {
39             if (L[i]>=X) continue;
40             if (R[i]==X && Y<=T[i] && B[i]<=yt) ok=false;
41             int yL=cmp(B[i], T[i], calc(vy, L[i]/vx));
42             int yR=cmp(B[i], T[i], calc(vy, R[i]/vx));
43             int xH=cmp(L[i], R[i], vx*(vy/g));
44             int yH=cmp(B[i], T[i], calc(vy, vy/g));
45             if (xH==0 && yH>=0 && yL<0) ok=false;
46             if (yL*yR<=0) ok=false;
47         }
48         if (ok) return true;
49     }
50     return false;
51 }
52 
53 int min(int x, int y)
54 {
55     if (x<y) return x;
56     return y;
57 }
58 
59 int main()
60 {
61     scanf("%d %d %d %d", &N, &V, &X, &Y);
62     for (int i=0; i<N; i++)
63     {
64         scanf("%d %d %d %d", &L[i], &B[i], &R[i], &T[i]);
65     }
66     for (int i=0; i<N; i++)
67     {
68         R[i]=min(R[i], X);
69     }
70     bool ok=check(X,Y);
71     for (int i=0; i<N; i++)
72     {
73         ok |= check(L[i], T[i]);
74         ok |= check(R[i], T[i]); 
75     }
76     puts(ok ? "Yes" : "No");
77 }

White Bird

注：像这样在几何问题中，当可行解可以取连续一段的值时，很多时候只要考虑边界的极限情况就能够顺利解决问题了。

平面扫描

Coneology(POJ 2932)

原题如下：
Coneology

Time Limit: 5000MS Memory Limit: 65536K

Total Submissions: 4805 Accepted: 1067

Description

A student named Round Square loved to play with cones. He would arrange cones with different base radii arbitrarily on the floor and would admire the intrinsic beauty of the arrangement. The student even began theorizing about how some cones dominate other cones: a cone A dominates another cone B when cone B is completely within the cone A. Furthermore, he noted that there are some cones that not only dominate others, but are themselves dominated, thus creating complex domination relations. After studying the intricate relations of the cones in more depth, the student reached an important conclusion: there exist some cones, all-powerful cones, that have unique properties: an all-powerful cone is not dominated by any other cone. The student became so impressed by the mightiness of the all-powerful cones that he decided to worship these all-powerful cones.

Unfortunately, after having arranged a huge number of cones and having worked hard on developing this grandiose cone theory, the student become quite confused with all these cones, and he now fears that he might worship the wrong cones (what if there is an evil cone that tries to trick the student into worshiping it?). You need to help this student by finding the cones he should worship.

Input

The input le specifies an arrangement of the cones. There are in total N cones (1 ≤ N ≤ 40000). Cone i has radius and height equal to R_i, i = 1 … N. Each cone is hollow on the inside and has no base, so it can be placed over another cone with smaller radius. No two cones touch.

The first line of the input contains the integer N. The next N lines each contain three real numbers R_i, x_i, y_i separated by spaces, where (x_i, y_i) are the coordinates of the center of the base of cone i.

Output

The first line of the output le should contain the number of cones that the student should worship. The second line contains the indices of the cones that the student should worship in increasing order. Two consecutive numbers should be separated by a single space.

Sample Input
```
5
1 0 -2
3 0 3
10 0 0
1 0 1.5
10 50 50
```
Sample Output
```
2
3 5
```
分析：由于有任意两圆都没有公共点这一条件，要判断一个圆是否在其他圆的内部，只要判断其圆心是否在其他圆内即可。这样判断每个圆是否是最外层的复杂度为O(N)，因此很容易得到O(N²)复杂度的算法。而利用平面扫描技术可以得到更为高效的算法。
在几何问题中，经常利用平面扫描技术来降低算法的复杂度。所谓平面扫描，是指扫描线在平面上按给定轨迹移动的同时，不断根据扫描线扫过部分更新信息，从而得到整体所要求的结果的方法。扫描的方法，既可以从左向右平移与y轴平行的直线，也可以固定射线的端点逆时针转动。
对于这道题而言，我们在从左向右平移与y轴平行的直线的同时，维护与扫描线相交的最外层的圆的集合。从左向右移动的过程中，只有扫描线移动到圆的左右两端时，圆与扫描线的相交关系才会发生变化，因此我们先将所有这样的x坐标枚举出来并排好序。首先，当扫描线移动到某个圆的左端时，我们需要判断该圆是否包含在其他圆中，为此，我们只需从当前与扫描线相交的最外层的圆中，找到上下两侧y坐标方向距离最近的两个圆，并检查它们就足够了，因为，假设该圆被包含与更远的圆中，却不被包含于最近的圆中，就会得出两个圆相交的结论，而这与题目的条件不符，于是，只要用二叉查找树来维护这些圆，就能够在O(logn)时间内取得待检查的圆了。其次，当扫描线移动到某个圆的右端时，如果该圆已经包含于其他圆中就什么也不做，如果是最外层的圆就将它从二叉树中删去。综上，总的复杂度是O(nlogn)。

代码：

 1 #include <cstdio>
 2 #include <utility>
 3 #include <set>
 4 #include <vector>
 5 #include <algorithm>
 6 
 7 using namespace std;
 8 
 9 const int MAX_N=40000;
10 int N;
11 double x[MAX_N], y[MAX_N], r[MAX_N];
12 
13 bool inside(int i, int j)
14 {
15     double dx=x[i]-x[j], dy=y[i]-y[j];
16     return dx*dx+dy*dy<=r[j]*r[j];
17 }
18 
19 void solve()
20 {
21     vector<pair<double, int> > events;
22     for (int i=0; i<N; i++)
23     {
24         events.push_back(make_pair(x[i]-r[i], i));
25         events.push_back(make_pair(x[i]+r[i], i+N));
26     }
27     sort(events.begin(), events.end());
28     set<pair<double, int> > outers;
29     vector<int> res;
30     for (int i=0; i<events.size(); i++)
31     {
32         int id=events[i].second % N;
33         if (events[i].second<N)
34         {
35             set<pair<double, int> >::iterator it=outers.lower_bound(make_pair(y[id], id));
36             if (it !=outers.end() && inside(id, it->second)) continue;
37             if (it !=outers.begin() && inside(id, (--it)->second)) continue;
38             res.push_back(id);
39             outers.insert(make_pair(y[id], id));
40         }
41         else
42         {
43             outers.erase(make_pair(y[id], id));
44         }
45     }
46     sort(res.begin(), res.end());
47     printf("%d\n", res.size());
48     for (int i=0; i<res.size(); i++)
49     {
50         printf("%d%c", res[i]+1, i+1==res.size() ? ‘\n‘ : ‘ ‘);
51     }
52 }
53 
54 int main()
55 {
56     scanf("%d", &N);
57     for (int i=0; i<N; i++)
58     {
59         scanf("%lf%lf%lf", &r[i], &x[i], &y[i]);
60     }
61     solve();
62 }

Coneology

凸包

Beauty Contest(POJ 2187)

原题如下：
Beauty Contest

Time Limit: 3000MS Memory Limit: 65536K

Total Submissions: 42728 Accepted: 13233

Description

Bessie, Farmer John‘s prize cow, has just won first place in a bovine beauty contest, earning the title ‘Miss Cow World‘. As a result, Bessie will make a tour of N (2 <= N <= 50,000) farms around the world in order to spread goodwill between farmers and their cows. For simplicity, the world will be represented as a two-dimensional plane, where each farm is located at a pair of integer coordinates (x,y), each having a value in the range -10,000 ... 10,000. No two farms share the same pair of coordinates.

Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms.

Input

* Line 1: A single integer, N

* Lines 2..N+1: Two space-separated integers x and y specifying coordinate of each farm

Output

* Line 1: A single integer that is the squared distance between the pair of farms that are farthest apart from each other.

Sample Input
```
4
0 0
0 1
1 1
1 0
```
Sample Output
```
2
```
Hint

Farm 1 (0, 0) and farm 3 (1, 1) have the longest distance (square root of 2)
分析：显然，如果某个点在另外三个点组成的三角形的内部，那么它就不可能属于最远点对，因而可以删去。这样，最后需要考虑的点，就只剩下不在任意三个点组成的三角形内部的，所给点集中最外围的点了。这些最外围的点的集合，就是包围原点集的最小凸多边形的顶点组成的集合，称为原点集的凸包。因为顶点的坐标限定为整数，坐标值的范围不超过M的凸多边形的顶点数只有O((√M)^2/3)个，所以只要枚举凸包上的所有点对并计算距离就可以求得最远点对了。
求凸包的算法很多，求n个点集对应的凸包，只要O(nlogn)时间。
一种基于平面扫描法的Graham扫描算法：
首先，把点集按x坐标→y坐标的字典序升序排序，那么排序后的第一个和最后一个点必然是凸包上的顶点，它们之间的部分可以分成上下两条链分别求解。求下侧的链时只要从小到大处理排序后的点列，逐步构造凸包，在构造过程中的凸包末尾加上新的顶点后，可能会破坏凸性，此时只要将凹的部分的点从末尾出去就好了。求上侧的链也是一样地从大到小处理即可。排序的复杂度为O(nlogn)，剩余部分处理的复杂度为O(n)。
旋转卡壳法：
假设最远点对是p和q，那么p就是点集中(p-q)方向最远的点，而q是点集中(q-p)方向最远的点，因此，可以按照逆时针逐渐改变方向，同时枚举出所有对于某个方向上最远的点对(这样的点对又叫做对踵点对)，那么最远点对一定也包含于其中。在逐渐改变方向的过程中，对踵点对只有在方向等于凸包某条边的法线方向时发生变化，此时点将向凸包上对应的相邻点移动。另方向逆时针旋转一周，那么对踵点对也在凸包上转了一周，这样就可以在凸包顶点的线性时间内求得最远点对。
附一张示意图：

代码1：

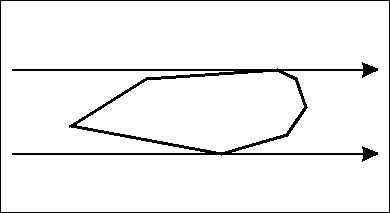
 1 #include <cstdio>
 2 #include <vector>
 3 #include <algorithm>
 4 #include <cmath>
 5 
 6 using namespace std;
 7 
 8 const double EPS=1e-10;
 9 
10 double add(double a, double b)
11 {
12     if (fabs(a+b)<EPS*(fabs(a)+fabs(b))) return 0;
13     return a+b;
14 }
15 
16 struct P
17 {
18     double x, y;
19     P(){}
20     P(double x, double y): x(x), y(y) {} 
21     P operator - (P p)
22     {
23         return P(add(x, -p.x), add(y, -p.y));
24     }
25     double det(P p)
26     {
27         return add(x*p.y, -y*p.x); 
28     }
29     double dot(P p)
30     {
31         return add(x*p.x, y*p.y);
32     }
33 };
34 
35 const int MAX_N=50005;
36 int N;
37 P ps[MAX_N];
38 
39 bool cmp_x(const P &p, P &q)
40 {
41     if (p.x!=q.x) return p.x<q.x;
42     return p.y<q.y;
43 }
44 
45 vector<P> convex_hull(P * ps, int n)
46 {
47     sort(ps, ps+n, cmp_x);
48     int k=0;
49     vector<P> qs(n*2);
50     for (int i=0; i<n; i++)
51     {
52         while (k>1 && (qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
53         qs[k++]=ps[i];
54     }
55     for (int i=n-2, t=k; i>=0; i--)
56     {
57         while (k>t && (qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
58         qs[k++]=ps[i];
59     }
60     qs.resize(k-1);
61     return qs;
62 }
63 
64 double max(int x, int y)
65 {
66     if (x>y) return x;
67     return y;
68 }
69 
70 double dist(P p, P q)
71 {
72     return (p-q).dot(p-q);
73 }
74 
75 int main()
76 {
77     scanf("%d", &N);
78     for (int i=0; i<N; i++)
79     {
80         scanf("%lf %lf", &ps[i].x, &ps[i].y);
81     }
82     vector<P> qs=convex_hull(ps, N);
83     double res=0;
84     for (int i=0; i<qs.size(); i++)
85     {
86         for (int j=0; j<i; j++)
87         {
88             res=max(res, dist(qs[i], qs[j]));
89         }
90     }
91     printf("%.0f\n", res);
92 }

Graham

代码2：

  1 #include <cstdio>
  2 #include <cmath>
  3 #include <algorithm>
  4 #include <vector>
  5 
  6 using namespace std;
  7 
  8 const double EPS=1e-10;
  9 
 10 double max(double x, double y)
 11 {
 12     if (x>y+EPS) return x;
 13     return y;
 14 }
 15 
 16 double add(double x, double y)
 17 {
 18     if (fabs(x+y)<EPS*(fabs(x)+fabs(y))) return 0;
 19     return x+y;
 20 }
 21 struct P
 22 {
 23     double x, y;
 24     P(){}
 25     P(double x, double y): x(x), y(y) {}
 26     P operator + (P p)
 27     {
 28         return P(add(x, p.x), add(y, p.y));
 29     }
 30     P operator - (P p)
 31     {
 32         return P(add(x, -p.x), add(y, -p.y));
 33     }
 34     double dot(P p)
 35     {
 36         return add(x*p.x, y*p.y);
 37     }
 38     double det(P p)
 39     {
 40         return add(x*p.y, -y*p.x);
 41     }
 42 };
 43 
 44 const int MAX_N=50005;
 45 int N;
 46 P ps[MAX_N];
 47 
 48 bool cmp_x(const P &p, const P &q)
 49 {
 50     if (p.x!=q.x) return p.x<q.x;
 51     return p.y<q.y;
 52 }
 53 
 54 double dist(P p, P q)
 55 {
 56     return (p-q).dot(p-q);
 57 }
 58 
 59 vector<P> convex_hull(P * ps, int n)
 60 {
 61     sort(ps, ps+n, cmp_x);
 62     int k=0;
 63     vector<P> qs(n*2);
 64     for (int i=0; i<n; i++)
 65     {
 66         while (k>1 && (qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
 67         qs[k++]=ps[i];
 68     }
 69     for (int i=n-2, t=k; i>=0; i--)
 70     {
 71         while (k>t && (qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
 72         qs[k++]=ps[i];
 73     }
 74     qs.resize(k-1);
 75     return qs;
 76 }
 77 
 78 int main()
 79 {
 80     scanf("%d", &N);
 81     for (int i=0; i<N; i++)
 82     {
 83         scanf("%lf %lf", &ps[i].x, &ps[i].y);
 84     }    
 85     vector<P> qs=convex_hull(ps, N);
 86     int n=qs.size();
 87     if (n==2)
 88     {
 89         printf("%.0f\n", dist(qs[0], qs[1]));
 90         return 0;
 91     }
 92     int i=0, j=0;
 93     for (int k=0; k<n; k++)
 94     {
 95         if (!cmp_x(qs[i], qs[k])) i=k;
 96         if (cmp_x(qs[j], qs[k])) j=k;
 97     }
 98     double res=0;
 99     int si=i, sj=j;
100     while (i!=sj || j!=si)
101     {
102         res=max(res, dist(qs[i], qs[j]));
103         if ((qs[(i+1)%n]-qs[i]).det(qs[(j+1)%n]-qs[j])<0)
104         {
105             i=(i+1)%n;
106         }
107         else
108         {
109             j=(j+1)%n;
110         }
111     }
112     printf("%.0f\n", res);
113 }

旋转卡壳

数值积分

Intersection of Two Prisms(AOJ 1313)

原题如下:
Suppose that P₁ is an infinite-height prism whose axis is parallel to the z-axis, and P₂ is also an infinite-height prism whose axis is parallel to the y-axis. P₁ is defined by the polygon C₁ which is the cross section of P₁ and the xy-plane, and P₂is also defined by the polygon C₂ which is the cross section of P₂ and the xz-plane.

Figure I.1 shows two cross sections which appear as the first dataset in the sample input, and Figure I.2 shows the relationship between the prisms and their cross sections.

Figure I.1: Cross sections of Prisms

Figure I.2: Prisms and their cross sections

Figure I.3: Intersection of two prisms

Figure I.3 shows the intersection of two prisms in Figure I.2, namely, P₁ and P₂.

Write a program which calculates the volume of the intersection of two prisms.

Input

The input is a sequence of datasets. The number of datasets is less than 200.

Each dataset is formatted as follows.

m n
x₁₁ y₁₁
x₁₂ y₁₂
.
.
.
x_1m y_1m
x₂₁ z₂₁
x₂₂ z₂₂
.
.
.
x_2n z_2n

m and n are integers (3 ≤ m ≤ 100, 3 ≤ n ≤ 100) which represent the numbers of the vertices of the polygons, C₁ and C₂, respectively.

x_1i, y 1 i, x _2j and z _2j are integers between -100 and 100, inclusive. ( x _1i, y _1i) and ( x _2j , z _2j) mean the i-th and j-th vertices‘ positions of C ₁ and C ₂respectively.

The sequences of these vertex positions are given in the counterclockwise order either on the xy-plane or the xz-plane as in Figure I.1.

You may assume that all the polygons are convex, that is, all the interior angles of the polygons are less than 180 degrees. You may also assume that all the polygons are simple, that is, each polygon‘s boundary does not cross nor touch itself.

The end of the input is indicated by a line containing two zeros.

Output

For each dataset, output the volume of the intersection of the two prisms, P₁ and P₂, with a decimal representation in a line.

None of the output values may have an error greater than 0.001. The output should not contain any other extra characters.

Sample Input
```
4 3
7 2
3 3
0 2
3 1
4 2
0 1
8 1
4 4
30 2
30 12
2 12
2 2
15 2
30 8
13 14
2 8
8 5
13 5
21 7
21 9
18 15
11 15
6 10
6 8
8 5
10 12
5 9
15 6
20 10
18 12
3 3
5 5
10 3
10 10
20 8
10 15
10 8
4 4
-98 99
-99 -99
99 -98
99 97
-99 99
-98 -98
99 -99
96 99
0 0
```
Output for the Sample Input
```
4.708333333333333
1680.0000000000005
491.1500000000007
0.0
7600258.4847715655
```
分析：朴素想法，求出公共部分的凸多面体的顶点坐标，然后再计算其体积。公共部分的凸多面体的顶点都是一个棱柱的侧面与另一个棱柱的侧棱的交点，可以通过O(nm)时间的枚举求得，但因为涉及三维空间的几何运算，实现起来是非常麻烦的。
事实上，沿x轴对棱柱切片即可：按某个值对侧棱与z轴平行的棱柱P₁切片后，就得到了[y₁,y₂]*(-∞,∞)这样的在z轴方向无限延伸的长方形的横截面，同样的，我们按某个x值对侧棱与y轴平行的棱柱P₂切片后，就得到了(-∞,∞)*[z₁,z₂]这样的在y轴方向无限延伸的长方形的横截面。因此，我们按某个x值对两个棱柱的公共部分切片后，得到的横截面就是长方形[y₁,y₂]*[z₁,z₂]。而长方形的面积通过(y₂-y₁)*(z₂-z₁)就可以求得，关于x轴对面积求积分就能得到公共部分的体积了。
首先，枚举出原棱柱底面顶点的所有x坐标并排序，在相邻两个x坐标之间的区间中按x值切片得到的长方形的顶点坐标是关于x的线性函数，所以面积就是关于x的二次函数，其积分很容易计算，虽然可以通过求得表达式后再来计算二次函数的积分，但应用Simpson公式则更为轻松。Simpson公式如下：

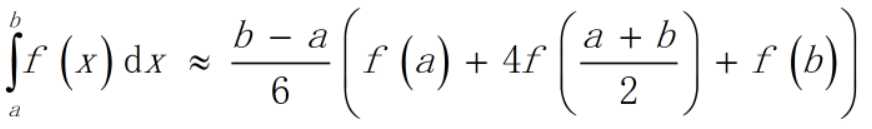
Simpson公式就是在数值积分中用二次函数来近似原函数进行积分而得到的公式，如果原函数本身就是次数不超过二的多项式，那么用Simpson公式就可以得到精确的积分值。利用该公式，无需求出关于x的多项式，而只要计算按区间的端点和中点切片得到的长方形的面积就够了。

代码：

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<vector>
 4 
 5 using namespace std;
 6 
 7 const int INF=0x3f3f3f3f;
 8 const double EPS=1e-10;
 9 const int MAX_N=500;
10 int N,M;
11 int X1[MAX_N], Y1[MAX_N], X2[MAX_N], Z2[MAX_N];
12 
13 double max(double x, double y)
14 {
15     if (x>y+EPS) return x;
16     return y;
17 }
18 
19 double min(double x, double y)
20 {
21     if (x<y-EPS) return x;
22     return y;
23 }
24 
25 double width(int * X, int * Y, int n, double x)
26 {
27     double lb=INF, ub=-INF;
28     for (int i=0; i<n; i++)
29     {
30         double x1=X[i], y1=Y[i], x2=X[(i+1)%n], y2=Y[(i+1)%n];
31         if ((x1-x)*(x2-x)<=0 && x1!=x2)
32         {
33             double y=y1+(y2-y1)*(x-x1)/(x2-x1);
34             lb=min(lb, y);
35             ub=max(ub, y);
36         }
37     }
38     return max(0.0, ub-lb);
39 }
40 
41 int main()
42 {
43     while (~scanf("%d %d", &M, &N))
44     {
45         if (M==0 && N==0) break;
46         for (int i=0; i<M; i++)
47         {
48             scanf("%d %d", &X1[i], &Y1[i]);
49         }
50         for (int i=0; i<N; i++)
51         {
52             scanf("%d %d", &X2[i], &Z2[i]);
53         }
54         int min1=*min_element(X1, X1+M), max1=*max_element(X1, X1+M);
55         int min2=*min_element(X2, X2+N), max2=*max_element(X2, X2+N);
56         vector<int> xs;
57         for (int i=0; i<M; i++) xs.push_back(X1[i]);
58         for (int i=0; i<N; i++) xs.push_back(X2[i]);
59         sort(xs.begin(), xs.end());
60         double res=0;
61         for (int i=0; i+1<xs.size(); i++)
62         {
63             double a=xs[i], b=xs[i+1], c=(a+b)/2;
64             if (min1<=c && c<=max1 && min2<=c && c<=max2)
65             {
66                 double fa=width(X1, Y1, M, a)*width(X2, Z2, N, a);
67                 double fb=width(X1, Y1, M, b)*width(X2, Z2, N, b);
68                 double fc=width(X1, Y1, M, c)*width(X2, Z2, N, c);
69                 res+=(b-a)/6*(fa+4*fc+fb);
70             }
71         }
72         printf("%.10f\n", res);
73     }
74 }

Intersection of Two Prisms

与平面和空间打交道的计算几何

标签：val 部分 element journey 字典 ping play ble 方便

原文地址：https://www.cnblogs.com/Ymir-TaoMee/p/9628746.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

Time Limit: 1000MS	Memory Limit: 10000K
Total Submissions: 5494	Accepted: 2504

Time Limit: 5000MS	Memory Limit: 65536K
Total Submissions: 4805	Accepted: 1067

Time Limit: 3000MS	Memory Limit: 65536K
Total Submissions: 42728	Accepted: 13233

与平面和空间打交道的计算几何

Input

Output

Sample Input 1

Output for the Sample Input 1

Sample Input 2

Output for the Sample Input 2

Sample Input 3

Output for the Sample Input 3

Input

Output

Sample Input

Output for the Sample Input