标签:one 出现 htm 传递 form png 计算 病毒 可见
1.信息技术概述
(1) 信息定义:信息即是对各种事物的变化和特征的反映,又是事物之间相互作用和联系的表征。
(2) 数据定义:数据是对某种情况的记录。信息和数据是有区别的,数据是携带信息的载体,而信息则是这个载体所携带的内容,经过加工处理后对管理决策和实现管理目标或任务具有参考价值的数据,是一种资源。
(3) 信息技术内容:信息技术(Information Technology,IT)是利用计算机处理、存储和传输信息的技术。
(4) 信息基础技术是信息技术的基础,包括新材料、新能源、新器件的开发和制造技术。近几十年来,影响最大的是微电子技术和光电子技术。
(5) 信息系统技术是指有关信息的获取、传输、处理、控制的设备和系统的技术。
(6) 信息获取技术:获取信息是利用信息的先决条件,例如传感技术、遥测技术、遥感技术等。
(7) 信息处理技术:信息处理技术是指对获取的信息进行识别、转换、加工,使信息安全地存储、传输,并能方便地检索、再生、利用,或便于人们从中提炼知识、发现规律的工作手段。
(8) 信息传输技术:就是指通信技术,是现代信息技术的支持。如信息光纤通信技术、卫星通信技术等。
(9) 信息控制技术:指利用信息传递和信息反馈来实现对目标系统进行控制的技术,如导弹控制技术等。在信息系统中,对信息实施有效的控制是利用信息的重要前提。
(10)信息应用技术:信息应用技术是针对种种实用目的,如信息管理、信息控制、信息决策而发展起来的具体的技术群类,如工厂自动化、办公自动化和互联通信技术等。
2.计算思维
思维是人脑运用分析、抽象、综合、概括等方法对现实事物进行研究从而揭露其本质的心理活动。一般而言,科学思维是经过感性认识获得大量素材,然后进行整理与改造,形成概念、判断和推理,以反映事物的本质与规律。
(1)理论思维。以推理和演绎为特征,以数学学科为代表。正如数学一样,定义是理论思维的灵魂,定理和证明是它的精髓。公理化方法是最重要的理论思维方法。
(2)实验思维。以观察和总结自然规律为特征,以物理学科为代表。它往往需要借助于某些特定的设备,并用它们来获取数据以供分析。
(3)计算思维。以设计和构造为特征,以计算机学科为代表。是运用计算机科学的基础概念去求解问题、设计系统和理解人类行为的一系列思维活动。
3.计算机用户的社会责任
(1)保护知识产权
(2)维护计算机系统安全
(3)加强网络道德建设, 遵守网络行为规范,具体做到:
4.数制
什么是数制:应用一组符号和一套统一的规则来表示数目的方法称为数制(Number System)。不同的数制间可以进行进制转换。
可以从下面三个方面来加深理解:
虽然计算机能极快地进行运算,但其内部并不像人类在实际生活中使用的十进制,而是使用只包含0和1两个数值的二进制。当然,人们输入计算机的十进制被转换成二进制进行计算,计算后的结果又由二进制转换成十进制,这都由操作系统自动完成,并不需要人们手工去做,学习汇编语言,就必须了解二进制(还有八进制/十六进制)。
(1)数码:数制中表示基本数值大小的不同数字符号。例如,十进制有10个数码:0、1、2、3、4、5、6、7、8、9。
(2)基数: 一个计数制所包含的数字符号的个数。如:十进制有(0,1,2,…,9)等数字符号,所以基数为10。
(3)位权值:一个数中的每一位数码所表示的实际值,不仅与数码本身的数值有关,还与所在的位置有关,由位置决定的值就叫位权值(简称位权)。
例如:十进制的123,1的位权是100,2的位权是10,3的位权是1。二进制中的 1011 ,第一个1的位权是8,0的位权是4,第二个1的位权是2,第三个1的位权是1
(4)数制:计数的规则。在人们使用最多的进位计数制中,表示数的符号在不同的位置上时所代表的数的值是不同的。
(5)十进制:人们日常生活中最熟悉的进位计数制。在十进制中,数用0,1,2,3,4,5,6,7,8,9这十个符号来描述。计数规则是逢十进一。
(6)二进制:在计算机系统中采用的进位计数制。在二进制中,数用0和1两个符号来描述。计数规则是逢二进一,借一当二。
(7)十六进制:人们在计算机指令代码和数据的书写中经常使用的数制。在十六进制中,数用0,1,…,9和A,B,…,F(或a,b,…,f)16个符号来描述。计数规则是逢十六进一。
(8)数制符号:二进制B(binary),八进制O(octal),十进制D(decimal),十六进制H(hexadecimal)
5.二进制的算术运算
当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。因为数字计算机只能识别和处理由‘0’.‘1’符号串组成的代码。其运算模式正是二进制。二进制运算包括二进制逻辑运算和算术运算。
加法:二进制数的加法规则是:逢2进1。0+0=0; 1+0=1; 0+1=1; 1+1=10
减法:二进制数的减法规则是:“借一当二”。 0-0=0 1-0=1 1-1=0 0-1=1(向高位借位)。
乘法:二进制数的乘法特别简单,因为每一步只包括乘以 “1”或乘以“0”。二进制乘法规则是:0×0=0 1×0=0 0×1=0 1×1=1
除法:二进制的除法也很简单,因为所求的商每位不是“1”就是“0”。0÷0 = 0,0÷1 = 0,1÷0 = 0 (无意义),1÷1 = 1
6.二进制的逻辑运算
(1)逻辑数据: 在逻辑上可以代表真与假、是与非、对与错、有与无这种具有逻辑性的量称为逻辑数据。逻辑上用二进制的0和1代表这种逻辑数据
(2)逻辑运算:逻辑数据之间的运算称为逻辑运算,在计算机中,逻辑数据的值用于判断某个事件成立与否,成立为真,反之为假。用1代表真,0代表假。
计算机的逻辑运算的算术运算的主要区别是:逻辑运算是按位进行的,位与位之间不像加减运算那样有进位或借位的联系。
逻辑运算主要包括三种基本运算:逻辑加法(又称“或”运算)、逻辑乘法(又称“与”运算)和逻辑否定(又称“非”运算)。此外,“异或”运算也很有用。
(1)逻辑加法(“或”运算)
逻辑加法通常用符号“+”或“∨”来表示。逻辑加法运算规则如下:
0+0=0, 0∨0=0
0+1=1, 0∨1=1
1+0=1, 1∨0=1
1+1=1, 1∨1=1
从上式可见,逻辑加法有“或”的意义。也就是说,在给定的逻辑变量中,A或B只要有一个为1,其逻辑加的结果就为1;只有当两者都为0时逻辑加的结果才为0。
(2)逻辑乘法(“与”运算)
逻辑乘法通常用符号“×”或“∧”或“·”来表示。逻辑乘法运算规则如下:
0×0=0, 0∧0=0, 0·0=0
0×1=0, 0∧1=0, 0·1=0
1×0=0, 1∧0=0, 1·0=0
1×1=1, 1∧1=1, 1·1=1
不难看出,逻辑乘法有“与”的意义。它表示只当参与运算的逻辑变量都同时取值为1时,其逻辑乘积才等于1。
(3)逻辑否定("非"运算)
逻辑非运算又称逻辑否运算。其运算规则为:
0=1 “非”0等于1
1=0 “非”1等于0
(4)异或逻辑运算(“半加”运算)
异或运算通常用符号"⊕"表示,其运算规则为:
0⊕0=0 0同0异或,结果为0
0⊕1=1 0同1异或,结果为1
1⊕0=1 1同0异或,结果为1
1⊕1=0 1同1异或,结果为0
即两个逻辑变量相异,输出才1
7.数制之间的相互转换(二进制、八进制、十进制、十六进制之间的转换)
(1) 十进制数转成非十进制数 整数部分:用除基数r取余逆排法(先余为低,后余为高)。即:把一个十进制的整数不断除以所需要的基数r,直到商为0为止,取其余数并逆排(除r取余逆排法),就能够转换成以r为基数的数。小数部分:用乘基数r取整顺排法(先整为高,后整为低)。即:将一个十进制小数转换成 r进制小数时,将十进制小数不断地乘以r,直到满足精度要求或直到纯小数部分为零为止,取其整数顺排(乘r取整顺排法)。
应当注意,把十进制数转换成二进制时,对于整数均可用有限位二进制整数表示,但对于小数却不一定能用有限位的二进制小数表示。当乘2后使小数部分等于零时,转换结束;当乘2后小数部分总是不等于零,转换过程将是无限的。
对于既包含整数部分又包含小数部分的十进制数,如果要转换到其他进制,则分别对整数部分和小数部分采用前述方法,然后组合即是求得的结果。
(2)非十进制数转换成十进制数
非十进制转换成十进制的方法:把非十进制数各位按位权值展开后求和即可。
(3)二进制数转换成八、十六进制数
二进制数转换成八进制:整数从右向左三位并一位,不足部分左补0 ;小数从左向右三位并一位,不足部分右补0
二进制数转换成十六进制:整数从右向左四位并一位,不足部分左补0;小数从左向右四位并一位,不足部分右补0
8.计算机中数据的表示
(1)数值型数据
机器数:将在机器内存放的正、负号数值化的数称为机器数,机器数对应的实际数值称为机器数的真值。
机器数的三个特点:
(2)定点数的表示方法
定点数:小数点的位置是固定的,约定在某一固定位置上,所以称为定点数表示法。
定点小数:小数点的位置在最高数值位的前面,符号位的后面。定点小数是纯小数,即所表示的小数的绝对值均小于1
定点整数:小数点的位置约定在最低数值位的后面。
注意:小数点在存储单元中不占存储位。
定点整数分为有符号和无符号两种,对于有符号的整数,最高位就是符号位。对于无符号数,所有的数字都是有效数值。
(3)浮点数的表示法
浮点表示来源于数学中的指数表示形式:
N=M×RC。
例如: 十进制数(123)D可以写作0.123×103, 1.23×102
小数点的位置是可以变化的。
在计算机中,一个浮点数由两部分构成:阶码C和尾数M。底数R是事先约定的,在机器数中不出现。
阶码: 相当于指数,是一个带符号的整数,决定数的范围.
尾数: 为了便于计算机中小数点的表示,规定尾数的绝对值为大于0.1并且小于1的小数(规格化)。尾数表示数值的有效数字,决定数的精度。
任意二进制规格化浮点数的表示形式:N=±d×2±p
d为尾数,前面的±为数的符号。P为阶码,其前面的±为阶码的符号。
浮点数在计算机内的存储形式为:
阶符 阶码 数符 尾数
注意:
9.原码,反码,补码
对于一个数, 计算机要使用一定的编码方式进行存储。 原码, 反码, 补码是计算机存储一个具体数字的编码方式。
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号, 正数为0, 负数为1。比如,十进制中的数 +2 ,计算机字长为8位,转换成二进制就是[00000010]。如果是 -2 ,就是 [10000010] 。因为第一位是符号位,所以机器数的形式值就不等于真正的数值。例如上面的有符号数 [10000010],其最高位1代表负,其真正数值是 -2 而不是形式值130([10000010]转换成十进制等于130)。所以将带符号位的机器数对应的真正数值称为机器数的真值。
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值。
反码的表示方法是:正数的反码是其本身;负数的反码是在其原码的基础上, 符号位不变,其余各个位取反。
补码的表示方法是:正数的补码就是其本身;负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1。 (即在反码的基础上+1)
举例:
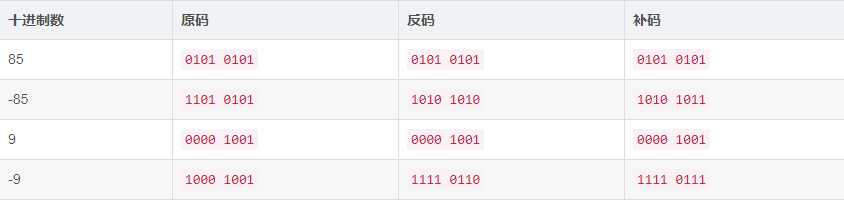
那么计算机为什么要使用补码呢?
首先,根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1+(-1), 所以计算机被设计成只有加法而没有减法, 而让计算机辨别”符号位”会让计算机的基础电路设计变得十分复杂,于是就让符号位也参与运算,从而产生了反码。
用反码计算, 出现了”0”这个特殊的数值, 0带符号是没有任何意义的。 而且会有[0000 0000]和[1000 0000]两个编码表示0。于是设计了补码, 负数的补码就是反码+1,正数的补码就是正数本身,从而解决了0的符号以及两个编码的问题: 用[0000 0000]表示0,用[1000 0000]表示-128。
注意-128实际上是使用以前的-0的补码来表示的, 所以-128并没有原码和反码。使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数。 这就是为什么8位二进制, 使用补码表示的范围为[-128, 127]。
标签:one 出现 htm 传递 form png 计算 病毒 可见
原文地址:https://www.cnblogs.com/hnust/p/9673791.html