标签:不同的 分组 ike sha tle 本质 技术分享 ima pow
2n个人排队买票,其中n个人持50元,n个人持100元。每张票50元,且一人只买一张票。初始时售票处没有零钱找零。请问这2n个人一共有多少种排队顺序,不至于使售票处找不开钱?
这个问题换而言之就是,服务过的持50的客户数量一定要大于等于持100的。解决的思路大致如下:

其实上面的解法本质就是卡特兰数:
所谓的卡特兰数就是满足下面式子:
![]()
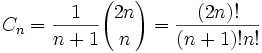
卡特兰数的前几项是1, 1, 2, 5, 14, 42, 132, 429, 1430
给你2*n个括号,当然是n个左括号,n个右括号,这样才能匹配。问有多少种匹配方式,
显然和上面的找零问题基本是完全一样的。完全符合卡特兰数的特征。
给你n个数,进栈的序列是1,2,3,4,…..n,有多少个不同的出栈次序
其实把入栈看成一个左括号,出栈看成一个右括号,那么上面这个问题又转化为上面的括号匹配的问题,所以又可以直接使用卡特兰数解决。
给定节点组成二叉树:给定n个点,能构成多少种不同的二叉树。
一个二叉树由三部分组成根节点,左子树,右子树。左子树的节点个数可能是0,1,2,3,…n-1,相应的右子树的节点个数可能是n-1,n-2,n-3,……3,2,1,0.由于左子树和右子树是独立的,
所以满足乘法原则。根据左子树的不同的节点数会产生不同的情况,满足加法原则所以f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0) 也符合卡特兰数
标签:不同的 分组 ike sha tle 本质 技术分享 ima pow
原文地址:https://www.cnblogs.com/linshuhui/p/9678180.html