标签:关于 动态规划 最短路径 最长路 比较 多个 有关 不同 情况下
转自:
动态规划的基本思想
动态规划的基本思想在于发现和定义问题中的子问题,这里子问题可也以叫做状态;以及一个子问题到下一个子问题之间 是如何转化的 也就是状态转移方程
因此我们遇到一个问题的时候 应该想一想这个问题是否能用某种方式表示成一个小问题,并且小问题具有最优子结构
最优子结构:问题的最优解由相关子问题的最优解组合而成,这些子问题可以独立求解
关于最优子结构 我们来看2个示例
1、求无权有向图中q-t的最短路径
如果q-t间的最短路径经过了点w 那么我们可以证明 q-w w-t也均是最短路径
所以无权有向图最短路径是具有最优子结构的
2、求无权有向图中q-t的最长的路径
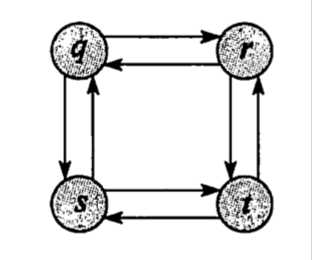
而无权有向图最长路径中
q-t的最长路径是是q-r-t 但 q-r缺不是q-r的最长路径 q-s-t-r是一条更长的路径
所以无权有向图最长路径不具有最优子结构
动态规划与贪心等其他算法的比较
动态规划与分治,减治
分治 :将大问题分成若干个小问题去解决 递归的求解每个小问题,每个小问题之间没有关系 例如 快排
减治 :将大问题缩减成小问题,减掉的部分不需要考虑,例如:二分查找
动态规划:将原问题分成多个子问题,不同子问题间存在一定的联系,相互间有重叠的子问题
这里我个人认为动态规划分治 减治都是将大问题拆分成小问题 进行求解 区别在于
减治法减掉的部分 可以不用再求解了;
分治法每个小问题都需要进行求解;
动态规划不同的子问题间是有相互重叠的子问题的
动态规划与贪心
动态规划在于我们求解了所有子问题 虽然有些子问题最终并不能组成答案
而贪心算法任务无需求解所有子问题,所以选择在当前情况下最优的情况自顶向下的求解问题,贪心可以认为是动态规划的一个特例
如果用一个树来表示子问题的话 可以认为动态规划考虑了树中的所有节点
而贪心算法减去了树了许多枝干,在考虑了通向最优解的那一条路
标签:关于 动态规划 最短路径 最长路 比较 多个 有关 不同 情况下
原文地址:https://www.cnblogs.com/jing-yu/p/9678291.html