标签:get family color span 方案 open tar class aik
上午noi.ac崩崩崩了,栽在组合数学上,虽说最后在辰哥&Chemist的指导下A掉了此题,也发现自己组合数学太弱了qwq。
在luogu上找题,结果找到了一个第二类斯特林数的题(还是双倍经验,逃。)
第二类斯特林数 S(n,k):把 n 个元素划分成 k 个集合的方案数。
这个问题说的实际一点,就比如说,有n个互异的小球,把他们放入m个盒子里,盒子里不允许为空的方案数。我们设s(i,j)表示放到i个小球,j个盒子的方案数。
那么对于每个小球,当前我们有两种放法:
第一种,我们把它放进一个现在盒子里没球的盒子中,这部分是s(i-1,j-1)
第二种,我们把它放进一个现在盒子里有球的盒子中,因为有j个盒子,所以这部分是 j * s (i-1,j)
那么将二者 加起来就是我们要求的解。
即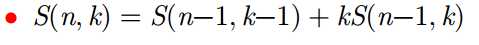
LuoguP3904三只小猪 比较裸啦=w=。

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 typedef long long ll; 6 7 ll n,m; 8 int len; 9 int ans[1000]; 10 int s[100][100][1000]; 11 12 ll lmin(ll a,ll b) 13 { 14 if(a<b) return a; 15 else return b; 16 } 17 18 void bigcalc(int x,int y) 19 { 20 if(y>x) return ; 21 if(x==1&&y==1) return ; 22 int tmp=0; 23 for(int i=1;i<=len;i++) ans[i]=0; 24 len=1; 25 for(int i=1;i<=s[x-1][y][0];i++) 26 { 27 ans[i]=s[x-1][y][i]*y+tmp; 28 tmp=ans[i]/10; 29 ans[i]%=10; 30 } 31 len=s[x-1][y][0]; 32 if(tmp) ans[++len]=tmp; 33 s[x][y][0]=1; 34 tmp=0; 35 while(s[x][y][0]<=s[x-1][y-1][0]||s[x][y][0]<=len) 36 { 37 s[x][y][s[x][y][0]]=s[x-1][y-1][s[x][y][0]]+ans[s[x][y][0]]+tmp; 38 tmp=s[x][y][s[x][y][0]]/10; 39 s[x][y][s[x][y][0]]%=10; 40 s[x][y][0]++; 41 } 42 s[x][y][s[x][y][0]]=tmp; 43 if(s[x][y][s[x][y][0]]==0&&s[x][y][0]!=1) s[x][y][0]--; 44 } 45 46 int main() 47 { 48 scanf("%lld%lld",&n,&m); 49 if(n<m) {printf("0");return 0;} 50 if(n==m) {printf("1");return 0;} 51 s[1][1][0]=1;s[1][1][1]=1; 52 for(int i=2;i<=n;i++) 53 for(int j=1;j<=lmin(i,m);j++) 54 bigcalc(i,j); 55 for(int i=s[n][m][0];i>=1;i--) 56 printf("%d",s[n][m][i]); 57 return 0; 58 }
LuoguP1655小朋友的球 上面题的二倍经验

(来自baidubaike==)
标签:get family color span 方案 open tar class aik
原文地址:https://www.cnblogs.com/nopartyfoucaodong/p/9690393.html