标签:结合 code 传递 合并 alt 复杂度 压缩 upload 修改
并查集(Disjoint-Set)是一种优美的数据结构,它擅长动态维护若干交集为空的集合,并且支持快速合并两个集合以及查找某个元素所在的集合。
然而这只是并查集所能做的一点微小的工作,文文对并查集的理解是“一种能够在线维护不同个体之间不可删除的关系并将其传递给之后加入的个体的优美的数据结构”。
光是听文文这么说,还是很抽象的,我们不妨来一步一步“发明”并查集吧!
你一天闲得无聊,想要发明一种数据结构。
首先,你想维护不同集合的合并与查询,于是你决定先找一种方法表示集合。显然的,你有了两种思路:
1.维护一个数组 \(f\) ,用 \(f[x]\) 表示元素 \(x\) 所在集合的代表,这样子的话,你可以快速查询一个元素的所属集合。
但是机灵的你又想到:如果你要合并两个集合,岂不是要修改很多f数组里的值吗?

2.用一棵树形结构储存每个集合,树上的每一个节点都代表一个元素,而每一棵树的树根就作为这个集合的代表元素。
每次合并两个集合的时候,只需要把一棵树的树根作为另一棵树树根的儿子就好了。你美滋滋的以为自己解决了这个数据结构,直到文文给你拿来了一张极不优美的图片。
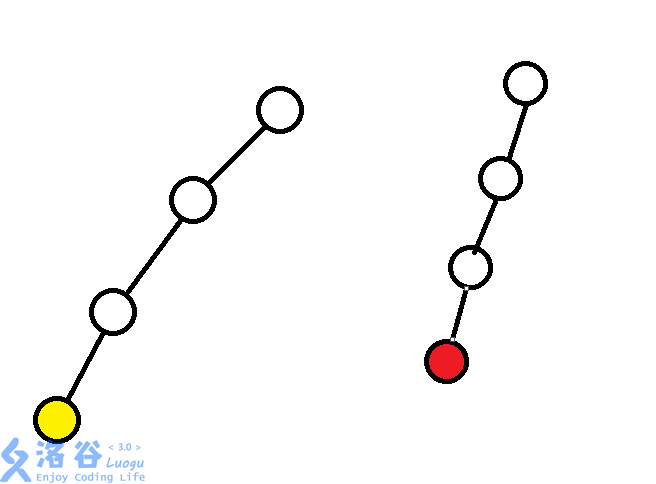
合并黄色节点以及红色节点所在集合,于是你的数据结构只好一个一个像链表一样,往上跳,跳到树根,你觉得这种跳法不优美。
你感觉非常悲伤,以为自己的数据结构要泡汤了,但是文文给了你一个思路:不如结婚结合之前的两种做法,让他们稍微平衡一下。
你看了看第一种方法,发现他就对应第二种方法里的这张图:
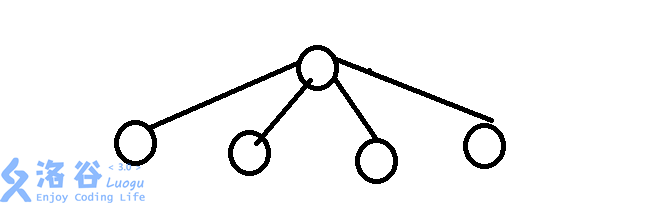
而一个一般的树形结构,是这样的:
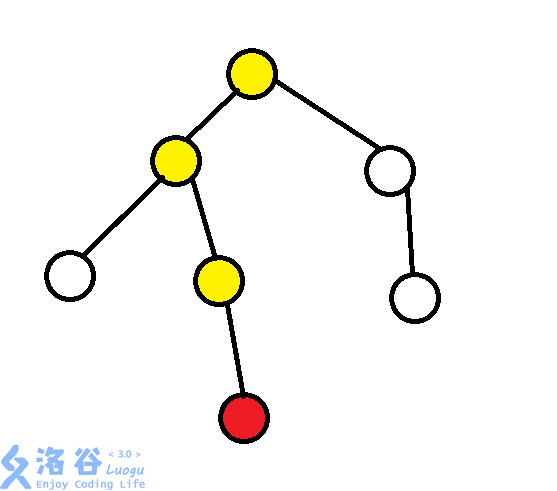
当我们想访问红色节点时,我们会沿着黄色节点,一步步跳上来。这个过程不是太优美,并且如果我们多次访问红色节点,这条路会走很多次。诶,等等!走很多次?这里好像有点搞头啊。
我们不如从这里优化:每次访问时,没有利用到之前访问时的信息。我们考虑让每个边只走一遍,那么我们就应该把走过的边废除掉!我们不妨沿路让经过的边统统废除,经过的点指向根。
上面这张图,查询过以后,就变成这样:
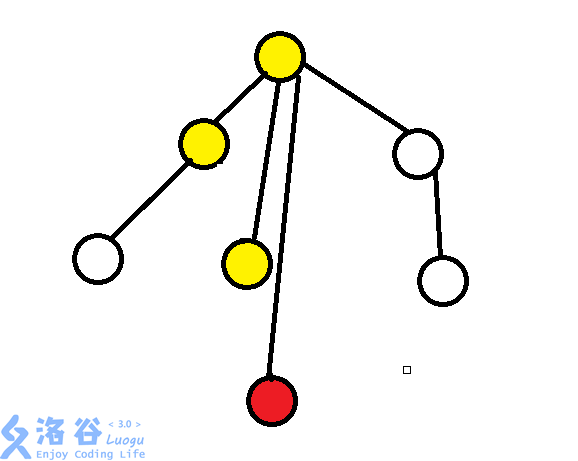
感觉这样,好像变成了玄学复杂度?实际上是均摊\(O(nlogn)\)的 .
感觉是log级别的吧,你们可以试试闭眼证明法(图片来自cdcq)

好了,不开玩笑,这个证明起来确实是\(O(logn)\)级别的,但是这个证明相当繁琐,有兴趣的话可以去搜索相关论文。
当然,聪明的你怎么可能只想到了一种方法呢?你又想到了另一个优化的方法——按秩合并。“秩”一般定义为集合的大小或者集合的深度。
当秩被定义为集合的大小时,按秩合并又被称为“启发式合并”。启发式合并在很多地方上都有体现,应用非常广泛。
我们每次按秩合并,把秩小的集合合并到秩大的集合,这样子,对秩大的集合没有影响,只影响秩小的集合。每次小的集合,向上跳一个,大小至少翻倍,所以最多跳\(log\)次,时间复杂度\(O(logn)\)。
我们考虑把之前所说的两种优化结合起来,即同时使用按秩合并+路径压缩(就是第一种方法的规范名称)。这个就真的成玄学时间了?但是著名科学家tarjan在1975年发表了一篇论文《Efficiency of a Good But Not Linear Set Union Algorithm》,证明了每次查询均摊复杂度为\(O(alpha(n))\) 其中,\(alpha\)是反阿克曼函数,证明对应所有的\(n< 2^{2^{10^{19729}}}\)都有\(alpha(n)<5\)
对于一般的题目,路径压缩或者按秩合并已经足够了,没必要结合起来。
那么你仔细思考了这个数据结构,他能合并和查询集合,于是给他起名为“并查集”。
你接下来打算用代码把刚才的内容实现一下(别哀嚎啦乖,很简单的)。
首先是初始化,我们还是用\(f\)数组,那么我们一开始,每个元素单独成一个集合,我们就这么做!
for(register int i=1;i<=n;++i) f[i]=i;你看,很简单对吧!
然后,考虑查询操作,我们用\(find\)来实现:
int find(int x) {
return f[x]==x ? x:fa[x]=find(fa[x]);
}嗯!上面这个代码用了一点小trick 他是等价于:
int find(int x) {
if(f[x]==x) return x;
f[x]=find(f[x]);
return f[x];
}那么,我们合并的时候怎么合并呢?
void merge(int a, int b) {
int p1 = find(a),p2=find(b);
if(p1==p2) return;
f[p1]=p2;
return;
}呼,基本的框架终于搭起来了,你打算马上试一试这个数据结构,于是去切了点题。
题目推荐:洛谷P3367 P1551
但是,你突然在一道题前面停下了脚步:银河英雄传说(洛谷P1196)。
这道题,貌似不能用之前太过于单纯的并查集维护了啊!
别急,遇事不决找文文,文文又来给你的并查集升级了哦~
并查集是一个树状结构,那么他也是有点和边的。咱考虑把边加上权值,表示两个元素之间的关系哦~
我们维护一个数组\(d\),数值\(d[x]\)表示节点\(x\)与其父节点的关系!
每次路径压缩以后,我们都要同时维护\(f[x]\)和\(d[x]\),这就是所谓的边带权。
什么是扩展域呢?问得好!(谜之音:我没问啊喂)
扩展域,顾名思义,我们原始并查集只有\(n\)个点,用来表示原本的元素,我们不妨创建\(2n\)个节点,把他们分成两部分,维护两种集合。例如我们可以用\(f[x]\)表示元素\(x\)的同类,\(d[x]\)表示元素\(x\)的天敌。我们很快会见到扩展域的应用。
如果有幸的话,文文应该还会发表关于2-SAT的文章,到时候我们就可以研究一下并查集维护的这种关系的本质是什么了!
有了这两个强力的武器,你又可以做更多的题目了呢!
推荐题目:洛谷P1196 P2016 P1477 P3207
由于文文水平有限,本文有任何不足之处,欢迎指正,共同交流。
有任何不懂或疑惑之处,可以在luogu官方群(515055655)中搜索文文殿下,一同学习。
标签:结合 code 传递 合并 alt 复杂度 压缩 upload 修改
原文地址:https://www.cnblogs.com/Syameimaru/p/9692127.html