反向传播的推导

时间：2018-09-24 00:30:00 阅读：239 评论：0 收藏：0 [点我收藏+]

推导过程

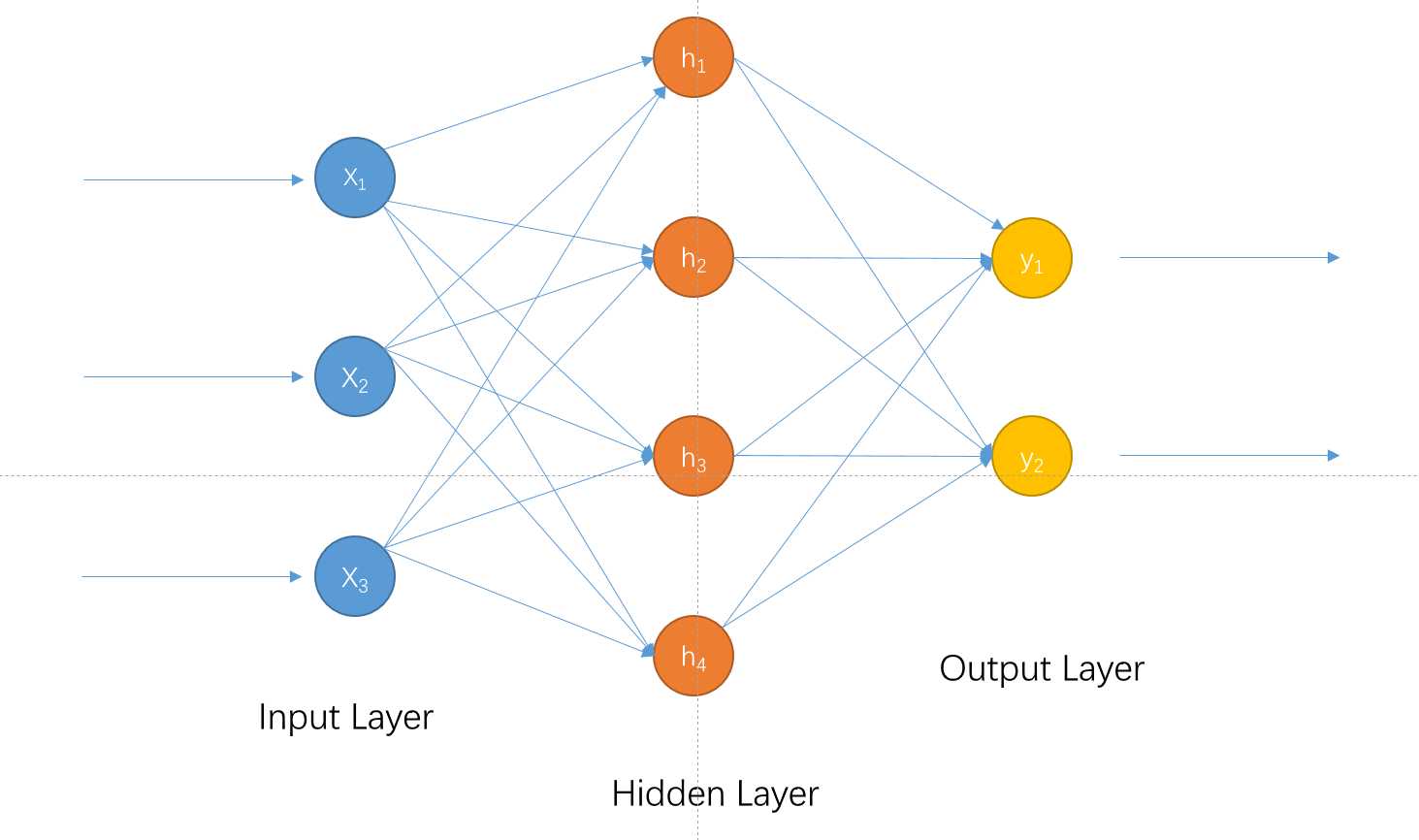
技术分享图片

如图中所示我们规定$W_{ij}^k$表示第k层与第k+1层之间神经元的权重值，$z^k$表示对应输入第k层的值，$o^k$表示对应第k层输出的值

定义损失函数为：

$l = \frac{1}{2}(y-\widehat{y})^2$($y$表示预期输出)

比如图中第2层和第3层的误差分配如下：

$ l_{23} =\begin{equation}\left(\begin{array}{ccc} w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\\w_{41}&w_{42} \end{array}\right)\left(\begin{array}{ccc}l_1\\l_2 \end{array}\right)\end{equation}$（省去$w$的上角标）

我们可以发现：此处的权重矩阵就是前向传播的时候第2层所乘的矩阵的转置矩阵，也就是$(w^k)^T$

引出记号：

$\frac{\partial L}{\partial W^k}$（表示损失函数的值是如何根据权重矩阵变化的）

则损失函数改写为：

$L = \sum_{i=1}^{n}\frac{1}{2}(y-\widehat{y})^2$

暂时把$\sum$忽略可得：

$\frac{\partial L}{\partial W^k}=\frac{\partial }{\partial W^k}\frac{1}{2}(y-\widehat{y})^2$

又根据链式法则：

$\frac{\partial L}{\partial W^k}=\frac{\partial L}{\partial \widehat{y}}·\frac{\partial \widehat{y}}{\partial z^{k+1}}·\frac{\partial z^{k+1}}{\partial W^k}$（$y_i$为激活函数）

如果取激活函数为sigmoid函数可得其导函数为：

$\sigma(x) = \frac{1}{1+e^{-x}}$ $\sigma‘(x) = \sigma(x)(1-\sigma(x))$

进一步改写得：

$\frac{\partial L}{\partial W^k}=-(y-\widehat{y})·\frac{\partial }{\partial W^k}\sigma(z^{k+1})$ $\frac{\partial L}{\partial W^k}=-(y-\widehat{y})·\sigma(z^{k+1})(1-\sigma(z^{k+1}))·\frac{\partial }{\partial W^k}\sigma(z^{k+1})$ $\frac{\partial L}{\partial W^k}=-(y-\widehat{y})·\sigma(z^{k+1})(1-\sigma(z^{k+1}))·o^k$ $\frac{\partial L}{\partial W^k}=(o^k)^T·(-(y-\widehat{y})·\sigma(z^{k+1})(1-\sigma(z^{k+1})))$

依次倒推回去即可

注：以上图的网络为例，$z^{k+1}=o^kW^k$对$W^k$来说$o^k$就是斜率

反向传播的推导

标签：反向差分 oid 误差 .com art sum array 分享图片

原文地址：https://www.cnblogs.com/MartinLwx/p/9694060.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行